Terrestrische Refraktion
Als terrestrische Refraktion (auch Strahlenbrechung oder atmosphärische Refraktion genannt) wird die Brechung eines Lichtstrahls in der untersten Erdatmosphäre bezeichnet. Diese entsteht durch die Änderung des Brechungsindexes der Luft entlang des Strahlverlaufs infolge der mit der Höhe abnehmenden Luftdichte und bewirkt eine bogenförmige Krümmung des Strahls, die bei genaueren Vermessungen oder im physikalischen Labor als Korrektion („Reduktion“) an jedem gemessenen Vertikalwinkel angebracht werden muss. Diese Strahlkrümmung beträgt durchschnittlich 13 % der Erdkrümmung und erhöht die horizontale Sichtweite geringfügig.
Die astronomische Refraktion ist ein Spezialfall der terrestrischen Refraktion.
Sichtbare Wirkung der Strahlenbrechung

Da die Lichtstrahlen meist zur Erdoberfläche hin gekrümmt sind, lassen sie entfernte Gegenstände höher erscheinen als bei einem geraden Strahlverlauf. Die den Meereshorizont genau berührende auf- oder untergehende Sonne steht rein geometrisch noch bzw. schon zur Gänze darunter. Ihre (flach-)ovale Form entsteht dadurch, dass ihr unterer Rand stärker als ihr oberer nach oben abgelenkt ist; denn der Gradient der Luftdichte nimmt normalerweise mit der Dichte nach oben ab. Bodennahe warme Luftschichten können den Gradienten jedoch verringern, im Extremfall sogar umkehren. Dann sind die Lichtstrahlen nach oben gekrümmt, was bei flachem Einfallswinkel als eine Luftspiegelung erscheint. Umgekehrt ist in einer Inversionsschicht der Gradient erhöht.
Reguläre Refraktion
Der Radius der Strahlkrümmung r variiert bei großem Bodenabstand zwischen 40.000 bis 50.000 km.
Der Refraktionskoeffizienten k ist das Verhältnis des Krümmungsradius der Lichtbahn r zum mittleren Erdradius R = 6371 km.
Der mittlere Refraktionskoeffizienten ist k = 0,13. Die mittlere Krümmung der Lichtstrahlen beträgt rund 13 Prozent der Erdkrümmung. Dieser Wert passt gut zum Dichtegradienten und dem vertikalen Temperaturgradienten der Normatmosphäre und wurde seit 200 Jahren für die Reduktion der meisten geodätischen Höhenmessungen verwendet.
Mit dem Zentriwinkel ω vom Erdmittelpunkt zu den Standpunkten, also dem Quotienten aus der Strecke S zwischen den Standpunkten und mittlerem Erdradius R, ist der Refraktionswinkel (ρ)[1]
Die Refraktion variiert sehr stark, sie hängt von der aktuellen Dichteschichtung der Atmosphäre ab, genauer vom Gradienten der Feuchtigkeit, der Temperatur und des Druckes der Luft, sodass sie mittels meteorologischer Messungen entlang des Strahlweges berechnet werden kann. Für hochpräzise Vermessungsprojekte ist es notwendig, den Strahlverlauf genauer zu untersuchen, was auf mehrere Arten erfolgen kann: mittels detaillierter Messung der Strahlungsbilanz, durch den Aufbau eines 3D-Messfeldes für die Lufttemperatur oder mit Zweifarbenlaser-Messgeräten.
Auswirkungen auf Höhen-Messungen
Bei konstanter Krümmung der Lichtstrahlen nimmt der Refraktionswinkel (ρ) linear und der Höhenfehler quadratisch mit der Entfernung zu. Über einige hundert Meter liegt er im Bereich von einem Millimeter, über 10 Kilometer beträgt er etwa einen Meter.
Die relativ stabilen Verhältnisse der Strahlenbrechung hat schon Carl Friedrich Gauß untersucht, als er um 1800 den Auftrag zur Hannoverschen Landesvermessung erhielt. Die Refraktion wirkt sich nämlich besonders auf Höhenmessungen über große Entfernungen aus: Das Gauß’sche „große Dreieck“ hat Kantenlängen von 68, 84 und 106 Kilometern.

Tageszeitliche Temperaturschwankungen ergeben bei gemessenen Höhen Variationen bis zu 7 mm (bei S=100 m).[2]
Beim Nivellement fällt der Höhenfehler unter der Voraussetzung heraus, dass beim Vor- und Rückblick gleiche Zielweiten eingehalten werden und der Refraktionseinfluss symmetrisch über beide Visuren ist. Wegen der durch die terrestrische Refraktion beschränkten Genauigkeit insbesondere bei großen Zielweiten (trigonometrisches Nivellement) spielt in der modernen Landesvermessung die Satellitengeodäsie eine wichtige Rolle. Auch hier wirkt jedoch die terrestrische Refraktion in der unteren Atmosphäre, und auch hier wird versucht, durch Differenzverfahren gleichartige Anteile zu eliminieren.
Abgrenzung
Die astronomische Refraktion ist ein Spezialfall der terrestrischen Refraktion in dem Sinne, dass das angepeilte Objekt sich außerhalb der Atmosphäre befindet und meist praktisch unendlich weit entfernt ist.
In Bodennähe
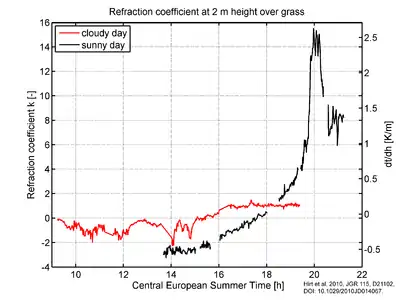
In Bodennähe (bis zu wenigen Metern über der Oberfläche) weicht der Refraktionskoeffizient häufig von 0,13 ab. Bei Bewölkung ist die Variation der Refraktion gering, bei starker Sonneneinstrahlung nimmt sie zu, auch Bodenbeschaffenheit und Beobachtungshöhe haben einen wesentlichen Einfluss. Der Refraktionskoeffizient nimmt Werte von −4 bis 15 an. Negative Werte werden insbesondere über heißen, spiegelnden Asphaltflächen erreicht.
Terrestrische Refraktion in der astronomischen Navigation
In der astronomischen Navigation wird mit einem Sextanten die Höhe eines Gestirns über dem Horizont gemessen. Auf Grund der Strahlenbrechung ist die wahre Höhe des Gestirns immer geringer als die mit dem Sextant gemessene Höhe, wobei der Effekt für kleine Höhen markanter ist. Die gemessene Höhe muss korrigiert werden. Unten stehende Tabelle[3] zeigt für 10 °C und den Normdruck (1013,2 hPa) die Zahl der Bogenminuten, die von der mit dem Sextanten gemessenen Höhe abgezogen werden muss. Vor allem bei geringen Höhen ist die Korrektur maßgebend, weil jede Bogenminute der Höhenmessung in der Ortsbestimmung zu einer Verschiebung der Position von einer Seemeile führt. Die hier beschriebene Korrektur der Strahlenbrechung ist eine der vier Beschickungen, die bei der Messung der Höhe des Gestirns durchgeführt werden müssen.
| Scheinbare Höhe | 0° | 1° | 2° | 3° | 4° | 5° | 6° | 7° | 8° | 9° | 10° |
| Brechung | 35.4' | 24.6' | 18.3' | 14.4' | 11.8' | 9.9' | 8.5' | 7.4' | 6.6' | 5.9' | 5.3' |
| Scheinbare Höhe | 12° | 14° | 16° | 20° | 30° | 40° | 50° | 60° | 70° | 80° | 90° |
| Brechung | 4.4' | 3.8' | 3.3' | 2.6' | 1.7' | 1.2' | 0.8' | 0.6' | 0.3' | 0.2' | 0.0' |
Literatur
- Heribert Kahmen: Angewandte Geodäsie – Vermessungskunde (= De-Gruyter-Lehrbuch). 20., völlig neu bearbeitete Auflage, de Gruyter, Berlin/ New York 2005, ISBN 3-11-018464-8.
- Karl Ramsayer: Geodätische Astronomie (= Handbuchs der Vermessungskunde. JEK Band IIa). Metzler, Stuttgart 1969 (siehe Refraktion: Kapitel 6, S. 107–140, und Anhang II, S. 832 ff.).
- Gottfried Gerstbach, M. Schrefl, W. Rössler: Bestimmung des Integralen Brechungsindex durch Befliegung des Meßstrahls. In: Österreichische Zeitschrift für Vermessungswesen und Photogrammetrie. Baden 1981 und 1982.
- Maria Hennes: Zum Refraktionseinfluss auf terrestrische geodätische Messungen im Kontext der Messtechnik und der Instrumentenentwicklung. In: FuB. 2002, Heft 2, S. 73–86 (Volltext als PDF; 758 kB).
- Christian Hirt, Sebastian Guillaume, Annemarie Wisbar, Beat Bürki, Harald Sternberg: Monitoring of the refraction coefficient of the lower atmosphere using a controlled set-up of simultaneous reciprocal vertical angle measurements. In: Journal of Geophysical Research. 2010, Band 115, doi:10.1029/2010JD014067 (Volltext bei Researchgate).
Weblinks
- Einfluss der terrestrischen Refraktion am Beispiel zweier Fernsichten auf die Alpen
- Winfried Lang: Die Alpensicht von der Kalmit in alter und neuer Bewertung (PDF; 166 kB) – Fernsichtberechnungen unter Einbezug singulär hoher Refraktionskoeffizienten.
Einzelnachweise
- Brunner, F.K., Wieser, A. (2009): „Skriptum Ingenieurgeodäsie“, Institut für Ingenieurgeodäsie und Messsysteme (IGMS), Technische Universität Graz, Folie 7-14
- Alexander Kukuvec Vertikaler Refraktionseffekt – Messung und Anwendung
- Auszug aus Otto Fulst: Nautische Tafeln. 24., erweiterte Auflage, Geist, Bremen 1972.