Metapopulation

Eine Metapopulation beschreibt eine Gruppe von Teilpopulationen (Subpopulationen), die untereinander einen eingeschränkten Genaustausch haben. Dabei besteht (i.GG. zu anderen Populationen, die sich aus Subpopulationen zusammensetzen) die Möglichkeit, dass Subpopulationen aussterben (lokale Extinktion) und an gleicher oder anderer Stelle Subpopulationen durch Neu- bzw. Wiederbesiedlung entstehen (lokale Kolonisation). Das Aussterben von Subpopulationen kann u. U. durch Immigration von Individuen aus anderen Subpopulationen verhindert werden (rescue-effect).

Es existieren mehrere Definitionen des Begriffes Metapopulation, die sich z. B. darin unterscheiden, ob es tatsächlich zu lokalen Extinktionen kommen muss, oder ob bereits die Möglichkeit lokaler Extinktionen (zu denen es dann aber z. B. aufgrund des Rescue-Effekts nicht kommt) für die Existenz einer Metapopulation genügt. Daneben gibt es je nach Definition weitere Voraussetzungen für die Existenz von Metapopulationen.

Mit Hilfe des Begriffs der Metapopulation lassen sich in der Populationsbiologie Vorgänge beschreiben, die sich zum einen auf einzelne Subpopulationen beziehen, zum anderen auf die Interaktionen mehrerer dieser Subpopulationen untereinander. Auf diese Weise entsteht eine mosaikartige Darstellung der Populationsdynamik, auf deren Basis der Genfluss ermittelt werden kann. Daneben findet die Metapopulationsökologie im Naturschutz Anwendung, da sich mit ihr Prozesse in fragmentierten Landschaften beschreiben lassen.

Metapopulationsmodell nach Levins

Bei der theoretischen Behandlung von Metapopulationen, deren Mitglieder über eine große Zahl von Habitaten verteilt sind, bedient man sich häufig eines räumlich impliziten Ansatzes. Nimmt man an, dass die Aussterbewahrscheinlichkeit in jedem einzelnen Habitat unabhängig vom Zustand der restlichen Habitate ist und die Kolonisationsrate linear von dem Anteil schon besetzter Habitate abhängt, gelangt man zu folgender Formulierung: Sei $p$ der Anteil der zum Zeitpunkt t besetzten Habitate (Patches) und e die Aussterbewahrscheinlichkeit bzw. c die Kolonisationswahrscheinlichkeit pro Zeitschritt. Dann ergibt sich:

(1)

{\frac {\mathrm {d} p}{\mathrm {d} t}}=cp(1-p)-ep

.

Wie man aus der Differentialgleichung ablesen kann, beträgt der Erwartungswert E der pro bewohntem Habitat neu oder wiederbesetzten Habitate ${\frac {c}{e}}$ . Gleichung (1) besitzt zwei stabile Fixpunkte, einen Fixpunkt bei $p*=0$ und einen weiteren Fixpunkt bei

(2)

p*=1-{\frac {e}{c}}

für

0<p<1

.

Verlust eines Teils L der zur Verfügung stehenden Habitate (also ${\frac {\mathrm {d} p}{\mathrm {d} t}}=cp(1-(p+L))-ep$ ) führt auf $E_{L}={\frac {c(1-L)}{e}}$ .

Wie für E diskutiert, liegt auch hier der Schwellenwert bei $E_{L}=1$ und somit bei $E=(1-L)^{-1}$ .

In letzter Konsequenz bedeutet dies, dass mehr Patches besiedelt werden müssen (damit p* > 0 muss gelten c > e), damit eine Metapopulation nicht ausstirbt. Das Levins-Modell bildet einen top-down-approach, da hier die Populationsdynamik pro Patch innerhalb der Metapopulationen weitestgehend vernachlässigt wird.

Anwendung

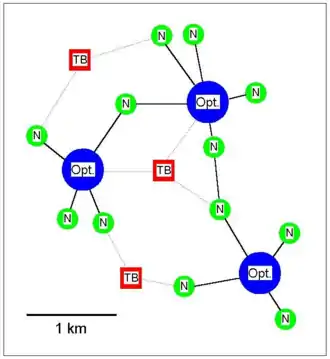
Schema eines idealisierten (virtuellen) Metapopulations-Modells aus Laubfroschgewässern verschiedener Güte und Priorität (Erläuterungen im Text)

Zur Darstellung der Anwendung wird hier das Metapopulationsmodell für den Europäischen Laubfrosch dargestellt. Dieser ist sehr stark von einer Verinselung seines Lebensraums durch Trockenlegung von Niedermooren und Gewässern sowie der Begradigung von Bächen und Flüssen betroffen.

Die großen blauen Kreise in der nebenstehenden Grafik stellen Optimalbiotope dar, die als Refugien und Ausbreitungszentren von individuenreichen „Überschusspopulationen“ fungieren. Durch Abwanderungen von dort werden suboptimale Nebenkolonien („N“) in deren Umfeld stabilisiert, so dass sich dort trotz individuell hoher Sterblichkeit kleinere Bestände halten können. Zusätzlich dienen „Trittsteinbiotope“ („TB“), die als Dauerlebensraum weniger geeignet sind, als biotopvernetzende temporäre Aufenthaltsorte für Individuen, die in der ansonsten intensiv bewirtschafteten Gegend umherwandern. Über Nebenkolonien und Trittsteinbiotope bestehen so zumindest mittelbar auch populationsökologische Wechselbeziehungen zwischen den Optimalbiotopen. Voraussetzung für das Funktionieren dieses Modells ist u. a. die „biologische Durchdringbarkeit“ der Landschaft: Amphibien„freundliche“ Linienstrukturen (Hecken etc.) spielen dabei eine wesentliche Rolle. Die Grafik verdeutlicht auch, dass der Wegfall bereits einzelner Neben- oder Trittsteinbiotope das Verbundnetz empfindlich beeinträchtigen oder unterbrechen kann. Wird sogar ein Optimalbiotop destabilisiert oder zerstört, ist davon das gesamte direkt verknüpfte Umfeld betroffen. Das Aussterberisiko erhöht sich auch hier wegen ausbleibender Zuwanderungen erheblich, obwohl es dort selbst keine qualitativen Veränderungen gegeben hat.

In der mathematischen Epidemiologie findet ein dem Metapopulationsansatz stark ähnelnder Formalismus unter dem Namen SIS-Modell breite Anwendung.

Literatur

R. Levins: Some demographic and genetic consequences of environmental heterogenity for biological control. In: Bull. Entomol. Soc. Am. 15, 1969, S. 237–240.
K. Sternberg: Populationsökologische Untersuchungen an einer Metapopulation der Hochmoor-Mosaikjungfer (Aeshna subarctica elisabethae Djakonov, 1922) im Schwarzwald. In: Z. Ökologie u. Naturschutz. 4, 1995, S. 53–60.
K. Sternberg: Regulierung und Stabilisierung von Metapopulationen bei Libellen, dargestellt am Beispiel von Aeshna subarctica elisabethae Djakonov, 1922 im Schwarzwald (Anisoptera, Aeshnidae). In: Libellula. 14, 1995, S. 1–39.
Ilkka Hanski: Metapopulation ecology. Oxford University Press, Oxford 1999, ISBN 0-19-854066-3.
Nicholas F. Britton: Essential Mathematical Biology. Springer, ISBN 1-85233-536-X.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.