Merge-Algorithmen
Merge-Algorithmen (von englisch merge ‚verschmelzen‘) sind eine Familie von Algorithmen, die mehrere sortierte Listen als Eingabe erhalten und eine einzelne sortierte Liste ausgeben, welche alle Elemente der Eingabelisten enthält. Merge-Algorithmen werden in vielen Algorithmen als Unterprogramm verwendet. Ein bekanntes Beispiel dafür ist Mergesort.
Anwendung
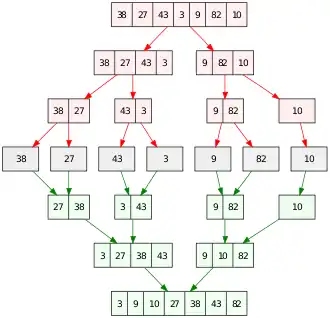
Der Merge-Algorithmus spielt eine wichtige Rolle im Mergesort Algorithmus, einem vergleichsbasierten Sortieralgorithmus. Konzeptionell besteht der Mergesort-Algorithmus aus zwei Schritten:
- Teile die Eingabe rekursiv in kürzere Listen von ungefähr gleicher Länge, bis jede Liste nur noch ein Element enthält. Eine Liste, welche nur ein Element enthält, ist nach Definition sortiert.
- Verschmilz wiederholt die kürzeren Listen, bis eine einzelne Liste alle Elemente enthält. Diese Liste ist nun die fertig sortierte Liste.
Der Merge-Algorithmus wird als Teil des Mergesort-Algorithmus immer wieder ausgeführt.
Ein Beispiel für Mergesort wird im Bild dargestellt. Man beginnt mit einer unsortierten Liste aus 7 Zahlen. Das Array wird in 7 Partitionen aufgeteilt, wovon jede nur ein Element enthält. Die sortierten Listen werden dann verschmolzen, um längere sortierte Listen zu liefern, bis nur noch eine sortierte Liste übrig ist.
Verschmelzen von zwei Listen
Das Verschmelzen von zwei sortierten Listen kann in linearer Zeitkomplexität und mit linearem Platz erfolgen. Der folgende Pseudocode zeigt einen Algorithmus, welcher zwei Listen A und B in eine neue Liste C verschmilzt.[1] Die Funktion kopf gibt das erste Element der Liste zurück. Entfernen des ersten Elements wird typischerweise über das Inkrementieren eines Pointers realisiert.
programm merge(A, B)
eingabe A, B : Liste
ausgabe Liste
C := neue leere Liste
solange A ist nicht leer und B ist nicht leer
wenn kopf(A) ≤ kopf(B) dann
hänge kopf(A) an C an
entferne den Kopf von A
sonst
hänge kopf(B) an C an
entferne den Kopf von B
// Entweder A oder B ist leer. Nun muss noch die andere Liste an C angehängt werden.
solange A ist noch nicht leer
hänge kopf(A) an C an
entferne den Kopf von A
solange B ist noch nicht leer
hänge kopf(B) an C an
entferne den Kopf von B
ausgabe C
Das Erstellen einer neuen Liste C kann vermieden werden. Dadurch wird der Algorithmus allerdings langsamer und schwerer zu verstehen.[2]
k-Wege-Mischen
Beim k-Wege-Mischen werden k sortierte Listen zu einer einzelnen, sortierten Liste verschmolzen, welche die gleichen Elemente wie die Ursprungslisten enthält. Sei n die Gesamtzahl der Elemente. Dann ist n die Größe der Ausgabe-Liste und auch die Summe der Größen der Eingabe-Listen. Das Problem kann in einer Laufzeit von O(n log k) und mit einem Platzbedarf von O(n) gelöst werden. Es existieren verschiedene Algorithmen.
Direktes k-Wege-Mischen
Die Idee von direktem k-Wege-Mischen ist es, das kleinste Element aller k Listen zu finden und an die Ausgabe anzuhängen. Eine naive Implementierung wäre es, in jedem Schritt alle k Listen zu durchsuchen, um das Minimum zu finden. Diese Lösung hat eine Laufzeit von Θ(kn). Dies funktioniert prinzipiell, ist allerdings nicht besonders effizient.
Die Laufzeit kann verbessert werden, indem das kleinste Element schneller gefunden werden kann. Über die Verwendung von Heaps oder Turnierbäumen (tournament trees) kann das kleinste Element in Zeit O(log k) gefunden werden. Die resultierende Zeit für das Verschmelzen liegt dann insgesamt in O(n log k).
Heaps werden in der Praxis häufig verwendet, allerdings besitzen Turnierbäume eine etwas bessere Laufzeit. Ein Heap benötigt etwa 2*log(k) Vergleiche in jedem Schritt, da er den Baum von der Wurzel nach unten zu den Blättern bearbeitet. Ein Turnierbaum dagegen benötigt nur log(k) Vergleiche, da er unten am Baum anfängt und sich mit nur einem Vergleich pro Ebene zur Wurzel nach oben arbeitet. Aus diesem Grund sollten Turnierbäume bevorzugt verwendet werden.
Heap
Der Heap-Algorithmus[3]
erstellt einen min-Heap mit Zeigern zu den Eingabelisten. Die Zeiger werden nach dem Element sortiert, auf welches sie zeigen. Der Heap wird durch einen heapify Algorithmus in einer Laufzeit von O(k) erstellt. Danach speichert der Algorithmus iterativ das Element, auf das der Wurzel-Zeiger zeigt, in die Ausgabe und führt einen increaseKey Algorithmus auf dem Heap aus. Die Laufzeit für den increaseKey Algorithmus liegt in O(log k). Da n Elemente zu verschmelzen sind, beträgt die gesamte Laufzeit O(n log k).
Turnierbaum
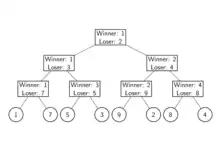
Der Turnierbaum (tournament tree)[4] basiert auf einem Turnier im K.-o.-System, wie es auch im Sport benutzt wird. In jedem Spiel treten zwei der Eingabe-Elemente gegeneinander an. Der Gewinner wird nach oben weitergegeben. Aus diesem Grund bildet sich ein Binärbaum aus Spielen. Die Liste wird hier in aufsteigender Reihenfolge sortiert, somit ist der Gewinner eines Spiels jeweils das kleinere der Elemente.
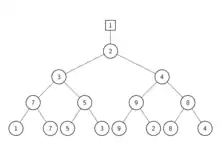
Beim k-Wege-Mischen ist es effizienter, nur den Verlierer jedes Spiels abzuspeichern (siehe Grafik). Die daraus resultierende Datenstruktur wird Verlierer-Baum (Loser tree) genannt. Beim Aufbau des Baums oder beim Ersetzen eines Elements wird trotzdem der Gewinner nach oben weitergegeben. Der Baum wird also gefüllt wie bei einem normalen Sport-Turnier, allerdings wird in jedem Knoten nur der Verlierer gespeichert. Normalerweise wird oberhalb der Wurzel ein zusätzlicher Knoten eingefügt, welcher den gesamten Gewinner speichert. Jedes Blatt speichert einen Zeiger zu einer der Eingabe-Listen. Jeder innere Knoten speichert einen Wert und einen Zeiger zu einer der Eingabe-Listen. Der Wert enthält eine Kopie des ersten Elements der zugehörigen Liste.
Der Algorithmus hängt iterativ das kleinste Element an die Rückgabe-Liste an und entfernt das Element dann von der zugehörigen Eingabe-Liste. Er aktualisiert dann alle Knoten auf dem Weg vom aktualisierten Blatt zur Wurzel (replacement selection). Das zuvor entfernte Element ist der gesamte Gewinner. Der Gewinner hat jedes Spiel auf dem Pfad zwischen Eingabe-Liste und Wurzel gewonnen. Wenn nun ein neues Element ausgewählt wird, muss dieses gegen die Verlierer der letzten Runde antreten. Durch die Verwendung eines Verlierer-Baums sind die jeweiligen Gegner bereits in den Knoten gespeichert. Der Verlierer jedes neu gespielten Spiels wird in den Knoten geschrieben und der Gewinner wird weiter nach oben in Richtung der Wurzel gegeben. Wenn die Wurzel erreicht wird, ist der gesamte Gewinner gefunden und es kann eine neue Runde des Verschmelzens gestartet werden.
Die Bilder von Turnierbaum und Verlierer-Baum in diesem Abschnitt verwenden dieselben Daten und können zum besseren Verständnis miteinander verglichen werden.
Algorithmus
Ein Turnierbaum lässt sich als perfekter Binärbaum darstellen, indem an jede Liste Sentinels hinzugefügt werden und die Anzahl der Eingabelisten durch leere Listen zu einer Zweierpotenz erweitert wird. Dann kann er in einem einzelnen Array dargestellt werden. Man erreicht das Eltern-Element, indem man den aktuellen Index durch 2 teilt.
Wird eines der Blätter aktualisiert, werden alle Spiele von diesem Blatt aus nach oben neu ausgetragen. Im folgenden Pseudocode wird zum einfacheren Verständnis kein Array verwendet, sondern ein objektorientierter Ansatz. Zusätzlich wird davon ausgegangen, dass die Anzahl der eingegebenen Folgen eine Zweierpotenz ist.
programm merge(L1, …, Ln)
erstelleBaum(kopf von L1, …, Ln)
solange Baum hat Elemente
gewinner := baum.gewinner
ausgabe gewinner.wert
neu := gewinner.zeiger.nächsterEintrag
spieleNeu(gewinner, neu) // Replacement selection
programm spieleNeu(knoten, neu) verlierer, gewinner := spiele(knoten, neu) knoten.wert := verlierer.wert knoten.zeiger := verlierer.zeiger wenn knoten nicht Wurzel spieleNeu(knoten.parent, gewinner)
programm erstelleBaum(elemente) nächsteEbene := new Array() solange elemente nicht leer el1 := elemente.take() // ein Element nehmen el2 := elemente.take() verlierer, gewinner := spiele(el1, el2) parent := new Node(el1, el2, verlierer) nächsteEbene.add(parent) wenn nächsteEbene.länge == 1 ausgabe nächsteEbene // nur Wurzel sonst ausgabe erstelleBaum(nächsteEbene)
Laufzeit
Der initiale Aufbau des Baums erfolgt in Zeit Θ(k). In jedem Schritt des Verschmelzens müssen die Spiele auf dem Pfad vom neuen Element zur Wurzel neu ausgetragen werden. In jeder Ebene ist nur eine Vergleichsoperation notwendig. Da der Baum balanciert ist, enthält der Pfad von Eingabe-Liste zur Wurzel nur Θ(log k) Elemente. Insgesamt müssen n Elemente übertragen werden. Die resultierende Gesamtlaufzeit liegt also in Θ(n log k).[4]
Beispiel
Der folgende Abschnitt enthält ein detailliertes Beispiel für das erneute Spielen (replacement selection) und ein Beispiel für einen gesamten Merge-Prozess.
Replacement selection
Spiele werden auf dem Weg von unten nach oben neu ausgetragen. In jeder Ebene des Baums treten das im Knoten gespeicherte Element und das von unten erhaltene gegeneinander an. Der Gewinner wird immer weiter nach oben gegeben, bis am Ende der gesamte Gewinner gespeichert wird. Der Verlierer wird im jeweiligen Knoten des Baums gespeichert.
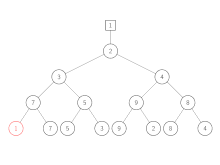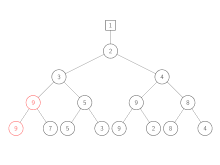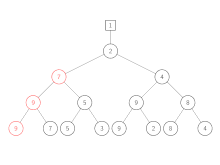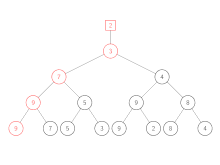
| Schritt | Aktion |
|---|---|
| 1 | Blatt 1 (gesamter Gewinner) wird durch 9, dem nächsten Element in der zugehörigen Eingabe-Liste, ersetzt. |
| 2 | Das Spiel 9 gegen 7 (Verlierer der letzten Runde) wird neu ausgetragen. 7 gewinnt, da es die kleinere Zahl ist. Aus diesem Grund wird 7 nach oben weitergegeben, während 9 im Knoten gespeichert wird. |
| 3 | Das Spiel 7 gegen 3 (Verlierer der letzten Runde) wird neu ausgetragen. 3 gewinnt, da es die kleinere Zahl ist. Aus diesem Grund wird 3 nach oben weitergegeben, während 7 im Knoten gespeichert wird. |
| 4 | Das Spiel 3 gegen 2 (Verlierer der letzten Runde) wird neu ausgetragen. 2 gewinnt, da es die kleinere Zahl ist. Aus diesem Grund wird 2 nach oben weitergegeben, während 3 im Knoten gespeichert wird. |
| 5 | Der neue gesamte Gewinner, 2, wird über der Wurzel gespeichert. |
Verschmelzen
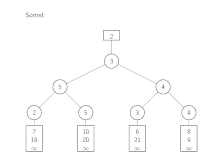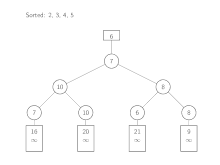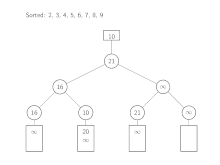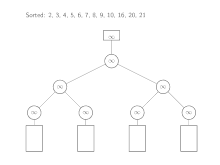
Zum eigentlichen Verschmelzen wird immer wieder das kleinste Element entnommen und mit dem nächsten Element der Eingabe-Liste ersetzt. Danach werden die Spiele bis zur Wurzel neu ausgetragen.
Als Eingabe werden in diesem Beispiel vier sortierte Arrays benutzt.
{2, 7, 16}
{5, 10, 20}
{3, 6, 21}
{4, 8, 9}
Der Algorithmus wird mit den Köpfen der Eingabelisten instanziiert. Aus diesen Elementen wird dann ein Baum aus Verlierern aufgebaut. Zum Verschmelzen wird das kleinste Element, 2, durch Lesen des obersten Elements im Baum bestimmt. Dieser Wert wird nun vom zugehörigen Eingabe-Array entfernt und durch den Nachfolger, 7, ersetzt. Die Spiele von dort aus zur Wurzel werden neu ausgetragen, wie es bereits im vorherigen Abschnitt beschrieben ist. Das nächste Element, das entfernt wird, ist 3. Beginnend mit dem nächsten Listenelement, 6, werden die Spiele wieder bis zur Wurzel neu ausgetragen. Dies wird so lange wiederholt, bis das gesamte Minimum oberhalb der Wurzel unendlich beträgt.
Laufzeitanalyse
Es kann gezeigt werden, dass kein vergleichsbasierter Algorithmus zum k-Wege-Mischen existieren kann, welcher eine schnellere Laufzeit als O(n log k) besitzt. Dies kann leicht durch Reduktion auf das vergleichsbasierte Sortieren bewiesen werden. Gäbe es einen schnelleren Algorithmus, könnte man einen vergleichsbasierten Sortieralgorithmus entwerfen, der schneller als O(n log n) sortiert. Der Algorithmus teilt die Eingabe in k=n Listen auf, die jeweils nur ein Element enthalten. Dann verschmilzt er die Listen. Wäre das Mergen in unter O(n log k) möglich, ist dies ein Widerspruch zum weit bekannten Ergebnis, dass für Sortieren im worst-case eine untere Schranke von O(n log n) gilt.
Paralleles Mischen
Eine parallele Version des binären Mischens dient als Baustein für einen parallelen Mergesort Algorithmus. Der folgende Pseudocode demonstriert einen parallelen Teile-und-Herrsche Mischalgorithmus (adaptiert von Cormen et al.[5]:800). Er operiert auf zwei sortierten Arrays und und schreibt den sortierten Output in das Array . Die Notation bezeichnet den Teil von von Index bis exklusive .
algorithm merge(A[i...j], B[k...ℓ], C[p...q]) is
inputs A, B, C : array
i, j, k, ℓ, p, q : indices
let m = j - i,
n = ℓ - k
if m < n then
swap A and B // ensure that A is the larger array: i, j still belong to A; k, ℓ to B
swap m and n
if m ≤ 0 then
return // base case, nothing to merge
let r = ⌊(i + j)/2⌋
let s = binary-search(A[r], B[k...ℓ])
let t = p + (r - i) + (s - k)
C[t] = A[r]
in parallel do
merge(A[i...r], B[k...s], C[p...t])
merge(A[r+1...j], B[s...ℓ], C[t+1...q])
Der Algorithmus beginnt, indem entweder oder (abhängig welches Array mehr Elemente enthält) in zwei Hälften aufgeteilt wird. Anschließend wird das andere Array in zwei Teile aufgeteilt: Der erste Teil enthält die Werte, die kleiner als der Mittelpunkt des ersten Arrays sind, während der zweite Teil alle Werte beinhaltet, die gleich groß oder größer als der Mittelpunkt sind. Die Unterroutine binary-search gibt den Index in zurück, wo wäre, wenn es in eingefügt wäre; dies ist immer eine Zahl zwischen und . Abschließend wird jede Hälfte rekursiv gemischt. Da die rekursiven Aufrufe unabhängig voneinander sind, können diese parallel ausgeführt werden. Ein Hybridansatz, bei dem ein sequentieller Algorithmus für den Rekursionsbasisfall benutzt wird, funktioniert gut in der Praxis[6].
Die Arbeit für das Mischen von zwei Arrays mit insgesamt Elementen beträgt . Dies wäre die Laufzeit für eine sequentielle Ausführung des Algorithmus, welche optimal ist, da mindestens Elemente in das Array kopiert werden. Um den Span des Algorithmus zu berechnen, ist es notwendig, eine Rekurrenzrelation aufzustellen und zu lösen. Da die zwei rekursiven Aufrufe von merge parallelisiert sind, muss nur der teurere der beiden Aufrufe betrachtet werden. Im schlimmsten Fall beträgt die maximale Anzahl an Elementen in einem Aufruf , da das größere Array perfekt in zwei Hälften aufgeteilt wird. Werden nun die Kosten für die binäre Suche hinzugefügt, erhalten wir folgende Rekurrenz:
.
Die Lösung ist . Dies ist also die Laufzeit auf einer idealen Maschine mit einer unbeschränkten Anzahl an Prozessoren[5]:801-802.
Achtung: Diese parallele Mischroutine ist nicht stabil. Wenn gleiche Elemente beim Aufteilen von und separiert werden, verschränken sie sich in , außerdem wird das Tauschen von und die Ordnung zerstören, falls gleiche Items über beide Inputarrays verteilt sind.
Einzelnachweise
- Steven Skiena: The Algorithm Design Manual, 2nd. Auflage, Springer Science+Business Media, 2010, ISBN 1-849-96720-2, S. 123.
- Jyrki Katajainen, Tomi Pasanen, Jukka Teuhola: Practical in-place mergesort. In: Nordic J. Computing. 3, Nr. 1, 1996, S. 27–40.
- Jon Louis Bentley: Programming Pearls, 2nd. Auflage, Addison-Wesley, 2000, ISBN 0201657880, S. 147–162.
- Donald Knuth: Chapter 5.4.1. Multiway Merging and Replacement Selection. In: Sorting and Searching (= The Art of Computer Programming), 2nd. Auflage, Band 3, Addison-Wesley, 1998, ISBN 0-201-89685-0, S. 252–255.
- Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford: Introduction to algorithms. Third edition Auflage. MIT Press, Cambridge, Mass. 2009, ISBN 978-0-262-27083-0.
- Victor J. Duvanenko: Parallel Merge. In: Dr. Dobb's Journal. 2011.
Siehe auch
- Donald Knuth. The Art of Computer Programming, Volume 3: Sorting and Searching, Third Edition. Addison-Wesley, 1997. ISBN 0-201-89685-0. Seiten 158–160 con Abschnitt 5.2.4: Sorting by Merging. Abschnitt 5.3.2: Minimum-Comparison Merging, Seiten 197–207.
- Mergesort