Somawürfel
Der Somawürfel ist ein mechanisches Geduldspiel, bei dem aus sieben einzelnen Teilen ein Würfel zusammengesetzt werden soll. Jedes einzelne Teil ist dabei ein Polywürfel, d. h., es ist selbst aus kleineren, jeweils identischen Würfeln zusammengesetzt, und alle sieben Teile sind (wie bei Pentominos) unterschiedlich.
Das Spiel dient der Schulung des räumlichen Vorstellungsvermögens ebenso wie der des Problemlösens.
Mögliche Aufgabenstellungen
Einen Würfel bauen
Der eine Triwürfel (Drilling) und die sechs Tetrawürfel (Vierlinge) des Spiels enthalten insgesamt der kleineren, jeweils identischen Würfel. John Horton Conway und Mike J.T. Guy fanden 1961 heraus, dass es für die Grundaufgabe des Spiels, die sieben Polywürfel zu einem 3x3x3-Würfel zusammenzusetzen, - bis auf Drehungen und Spiegelungen des Würfels - genau 240 verschiedene Lösungsmöglichkeiten gibt.[1][2] Wie Brunvoll et al.[3] genauer ausführen, kann man den Somawürfel auf genau 480 Arten, die durch Drehung des Somawürfels nicht ineinander überführt werden können, zusammensetzen; diese 480 Lösungen setzen sich aus 240 Paaren von jeweils zueinander spiegelsymmetrischen (d. h. ebenensymmetrischen) Lösungen zusammen.
Es gibt nur wenige Arten, die Polywürfel so zu einem 3x3x3-Würfel zusammenzusetzen, dass er nicht auseinanderfällt, wenn man den Würfel nur in der Mitte der Unterseite unterstützt („ausbalancierter Soma-Würfel“).[4]
Soma-Tangram
Beim Soma-Tangram muss ein Körper, gegeben durch ein Schrägbild, aus Soma-Teilen zusammengesetzt werden.[5][6]
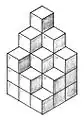Diamant
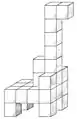Giraffe
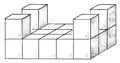umgedrehter Tisch
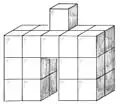Tor
Geschichte
Erfunden wurde der Somawürfel 1936 von Piet Hein während einer Vorlesung über Quantenmechanik von Werner Heisenberg.[7] Bekannt wurde der Würfel durch Martin Gardner, als er ihn 1958 in seiner Kolumne Mathematical Games in der Zeitschrift Scientific American besprach.[8] Seit die Schweizerischen Lehrkräfte und Fortbildner Ueli Hirt und Sandra Meister Unterrichtsmaterial für den Somawürfel ausarbeiteten und auf einer Tagung der Gesellschaft für Didaktik der Mathematik 2001 in Ludwigsburg vorstellten, wird er insbesondere im Mathematikunterricht der Grundschule gern eingesetzt.[9][10]
Der Asteroid des inneren Hauptgürtels (2815) Soma ist nach dem Somawürfel benannt.[11]
Zu den sieben Einzelteilen
Die sieben Einzelteile sind die sämtlichen möglichen irregulären Körper (Polywürfel), die aus drei oder vier Würfeln zusammengesetzt werden können. Irregulär heißt hierbei, dass mindestens eine einspringende Kante existiert (oder, anders gesagt, dass der Polywürfel nicht konvex ist). Daraus ergibt sich, dass es genau einen Dreier („v“) und sechs Vierer gibt. Bei den Vierern gibt es drei flache und drei 3D-Formen. Die flachen sind L-, S- und T-förmig.
Variation Babylonia
Zur Variation Babylonia des Somawürfel-Spieles gehören zwei Dreier- und sieben Viererbausteine. Die beiden Dreierbausteine sind schwarz und weiß, die Viererbausteine in den Farben Blau, Gelb, Grün, Orange, Rot und Violett sowie Natur. Ein W6-Würfel zeigt lediglich die Farben Schwarz und Weiß, ein bunter W6-Würfel zeigt alle vorgenannten Farben außer Natur. Nun gilt es mit den Würfeln die Farben zweier Bausteine zu bestimmen, die beim Bau des Somawürfels nicht verwendet werden sollen. Der naturfarbene Baustein ist immer zu verwenden.
Spielsteine und Würfel des Spieles Babylonia
Farbenwürfel des Spieles Babylonia
Literatur
- Elwyn R. Berlekamp; John H. Conway; Richard K. Guy: Gewinnen. Strategien für mathematische Spiele. Bd. 4: Solitairspiele. Braunschweig; Wiesbaden: Vieweg, 1985, S. 41–42 (Soma), 43–45 (Die verborgenen Geheimnisse von Soma), 107–110 (Die Somap).
- Martin Gardner: The Second Scientific American Book of Mathematical Puzzles and Diversions. New York: Simon and Schuster, 1961. ND Chicago: University of Chicago Press, 1987, Kap. 6, S. 65–77 (The Soma Cube).
Weblinks
- Somawürfel (Mathematische Basteleien)
- SOMA CUBE ANIMATION by TwoDoorsOpen and Friends
- Der ausbalancierte Soma Würfel, balanced soma cube
Einzelnachweise
- Elwyn R. Berlekamp, John H. Conway, Richard K. Guy: Winning Ways for Your Mathematical Plays, Vol. 2. Academic Press, London, 1982
- Soma Cube, Wolfram MathWorld
- Jon Brunvoll, Bjørg Cyvin, Einar Cyvin, Sven Cyvin, Aage Paus, Martin Stølevik, Reidar Stølevik: The computerized Soma cube. Computers & Mathematics with Applications, Vol. 12, 1986, S. 113–121
- Die 4. Lösung eines ausbalancierten Soma Würfel
- Soma-Figuren-Übersicht (pentoma.de)
- Dänemark: Der Soma-Würfel (Memento des Originals vom 23. Dezember 2016 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.. SAMMS - Schüler-Akademie Mathematik in Münster
- Martin Gardner: Mathematical puzzles and diversions Vol. 1/2. Simon and Schuster, New York, 1959/1961 (deutsch als Mathematische Rätsel und Probleme, Vieweg Verlag, 1964)
- Martin Gardner: A game in which standard pieces composed of cubes are assembled into larger forms. Scientific American, September 1958
- Ueli Hirt, Sandra Luginbühl: Spiele mit dem Somawürfel, Kallmeyer, 2003
- Dorothea Winkler: Karteien zum Soma-Würfel. Westermann Schulbuch Verlag, 2006
- Lutz D. Schmadel: Dictionary of Minor Planet Names. Fifth Revised and Enlarged Edition. Hrsg.: Lutz D. Schmadel. 5. Auflage. Springer Verlag, Berlin, Heidelberg 2003, ISBN 978-3-540-29925-7, S. 186 (englisch, 992 S., link.springer.com [ONLINE; abgerufen am 15. September 2019] Originaltitel: Dictionary of Minor Planet Names. Erstausgabe: Springer Verlag, Berlin, Heidelberg 1992): “1982 RL. Discovered 1982 Sept. 15 by E. Bowell at Anderson Mesa.”
