Linear rückgekoppeltes Schieberegister

Ein linear rückgekoppeltes Schieberegister (engl. linear feedback shift register, kurz LFSR) ist ein rückgekoppeltes Schieberegister, das zur Erzeugung von streng deterministischen Pseudozufallszahlenfolgen eingesetzt werden kann. Zur Rückkopplung wird die lineare logische Funktion XOR verwendet.

Ein 4-bit-Fibonacci-LFSR und seine Zustände. Das Register schiebt die Bits von links nach rechts. Das Exklusiv-Oder-Gatter wird von den beiden hinteren Bits des Registers gefüttert und liefert diesem vorne damit wiederum die Eingabe. Die maximale Ausgabesequenz besteht aus jedem möglichen Zustand mit Ausnahme des Zustands "0000".

Den Startwert bezeichnet man als seed. Da die Ausgabe des Registers streng deterministisch ist und vollständig von seinem momentanen Zustand abhängt, das Register jedoch gleichzeitig nur eine endliche Anzahl an Zuständen hat, muss es zwangsläufig irgendwann wieder bei seinem Startwert ankommen. Bei n Bit breiten Schieberegistern ergibt sich damit eine maximale Periodenlänge von 2ⁿ−1. Ab diesem Zeitpunkt wiederholt sich die Ausgabesequenz, das Register befindet sich in einem Wiederholzyklus. Je nach gewählter Implementierung ist diese Sequenz unterschiedlich lang, allerhöchstens können Folgen maximaler Länge erzeugt werden.

Anwendungen liegen neben der Erzeugung von Pseudozufallszahlenfolgen im Bereich schneller digitaler Synchronzähler, da diese Zähler ohne Übertrag arbeiten, im Bereich der Nachrichtentechnik und Kryptografie bei Scramblern, um Datenfolgen spektral weiß zu machen, in der Kodierungstheorie bei der Kodierung und Dekodierung von zyklischen Codes, wie beispielsweise bei der zyklischen Redundanzprüfung (CRC) oder dem Hamming-Code, und im Bereich der digitalen Modulationstechnik bei den Codemultiplexverfahren (CDMA) und im Bereich der Steganographie.

Linear rückgekoppelte Schieberegister können effizient sowohl direkt in Hardware, wie beispielsweise FPGAs, als auch in Software implementiert werden. Bei der Softwareimplementierung wird, da die meisten Prozessoren mit Registerbreiten größer als ein Bit arbeiten, typischerweise mit im Voraus berechneten Tabellen gearbeitet, die direkt den inneren Zustand des Schieberegisters abbilden.

Funktionsweise

Ein LFSR ist in der Digitaltechnik als ein Schieberegister mit n Speicherelementen realisiert. Die einzelnen Speicherelemente sind typischerweise D-Flipflops, welche je ein Bit speichern können. Im Gegensatz zu einem gewöhnlichen Schieberegister bestehen zwischen bestimmten D-Flipflops Abzweigungen, welche die Rückkopplungen darstellen. Die Anzahl und die Position dieser Abzweigungen in der Registerkette wird zur Erzielung der maximal möglichen Periodenlänge von 2ⁿ−1 durch ein primitives Polynom, das sogenannte Generatorpolynom, bestimmt. n ist in diesem Fall auch gleich dem Grad des Generatorpolynoms.

Ein primitives Polynom als Generatorpolynom ist nicht zwingend notwendig, allerdings ergeben nicht-primitive Polynome kürzere Periodenlängen. Kürzere Periodenlängen sind jedoch auch mit einer geringeren Anzahl von Flipflops und Verwendung eines entsprechenden primitiven Polynoms geringeren Grades erreichbar, weshalb als Generatorpolynome praktisch ausschließlich primitive Polynome Einsatz finden.

Zur Initialisierung, im Englischen wird dieser Startwert auch als seed bezeichnet, kann das Schieberegister mit XOR-Rückkopplung mit beliebigen Werten gefüllt werden – bei positiver Logik jedoch nicht nur mit Nullen, da dann das Register aus diesem Zustand niemals herauskäme, das Schieberegister also eine triviale Folge konstanter Nullen generieren würde. Es können statt der XOR-Verknüpfungen auch XNOR-Verknüpfungen eingesetzt werden (negative Logik); in diesem Fall sind als Startwert alle Werte außer lauter Einsen erlaubt, was auch wieder eine maximale Periodenlänge von 2ⁿ−1 ergibt. Je nach Technologie ist es einfacher, den Zustand mit lauter Nullen als definierten Anfangszustand zu implementieren. Die Verknüpfung mittels XNOR hat hierbei den Vorteil, dass dieser Zustand mit lauter Nullen als Startwert geeignet ist und nicht, wie bei XOR, zu der trivialen konstanten Nullfolge führt.

Ein LFSR kann auch so implementiert werden, dass es die maximale Periodenlänge von 2ⁿ aufweist. Hierbei treten nach einem Durchlauf lauter '0' im Schieberegister auf, die als Sonderfall durch eine zusätzliche Logikschaltung erkannt und durch daraufhin aktivierte Invertierung der Rückkopplung kompensiert werden müssen. Diese Möglichkeit besteht analog auch bei XNOR-Verknüpfungen; der Sonderfall ist hierbei stattdessen der Zustand mit lauter Einsen.

Wie jedes andere Schieberegister verfügt auch das LFSR über einen Takteingang: Bei jedem Taktimpuls wird in den Folgezustand gewechselt und für einen vollständigen Durchlauf aller Kombinationen sind 2ⁿ−1 Taktimpulse notwendig (sofern, wie oben beschrieben, ein primitives Polynom zum Einsatz kommt und auf das erwähnte „Aufbohren“ der Rückkopplung auf 2ⁿ Zustände verzichtet wurde).

Ein LFSR bildet wegen seiner Linearität der erzeugten Folgen für sich alleine für kryptologische Anwendungen einen schlechten Pseudozufallszahlengenerator. LFSR werden als Grundelement und in Verbindung mit nichtlinearen Funktionen oder als eine Kombination mehrerer LFSR verwendet.

Neben den in digitalen Schaltungen üblichen binären LFSR in GF(2) existieren auch nichtbinäre LFSR mit einer Anzahl an Elementen q größer als 2. Die XOR-Operation, sie stellt eine Addition modulo 2 dar, wird im allgemeinen Fall durch eine Addition modulo q ersetzt, die Speicherelemente müssen je q Zustände speichern können.

Arten

Es gibt in der Realisierung zwei verschiedene Arten von LFSR:

Fibonacci-LFSR, benannt nach dem italienischen Mathematiker Leonardo Fibonacci, und
Galois-LFSR, benannt nach dem französischen Mathematiker Évariste Galois.

Beide Typen sind zueinander gleichwertig und weisen die gleichen Periodenlängen auf, wenngleich die erzeugten Folgen unterschiedlich sind. Sie unterscheiden sich in der Realisierung, wie in den Abbildungen dargestellt, wobei CLK den Takteingang und Y den Ausgang des LFSR darstellen. Die XOR-Operatoren sind mit „ $\oplus$ “ dargestellt.

Fibonacci-LFSR

Galois-LFSR

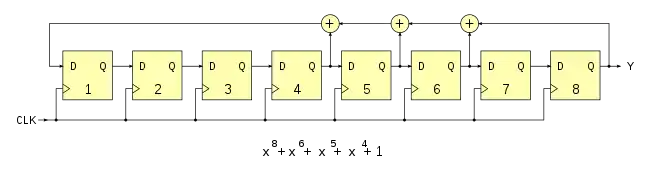
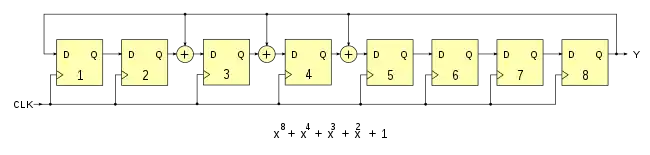
Die beiden Formen ergeben sich aus dem Umstand, dass jedes primitive Polynom vom Grad n > 2 ein „Zwillingspolynom“ besitzt, welches ebenfalls primitiv ist.[1] In den beiden Abbildungen wurde für das Fibonacci-LFSR ein Generatorpolynom vom 8. Grad verwendet:

p_{f}(x)=x^{8}+x^{6}+x^{5}+x^{4}+1

Die Abzweigstellen entsprechen direkt den Exponenten. Das dazu gleichwertige primitive Generatorpolynom vom 8. Grad im Galois-LFSR ist:

p_{g}(x)=x^{8-8}+x^{8-6}+x^{8-5}+x^{8-4}+x^{8-0}=x^{8}+x^{4}+x^{3}+x^{2}+1

Welche der beiden gleichwertigen Formen konkret gewählt wird, hängt unter anderem von Optimierungen bei der Implementierung ab. So können beispielsweise die drei Exklusiv-Oder-Gatter mit je zwei Eingängen in der Fibonacci-Struktur zu einem Exklusiv-Oder-Gatter mit vier Eingängen zusammengefasst werden. Diese Form lässt sich in FPGAs mit Lookup-Tabellen, welche vier Eingänge aufweisen, effizient implementieren.

Polynomauswahl

Neben dem Grad n, welcher die Periodenlänge festlegt, existieren bei einem bestimmten Grad n > 2 immer mehrere primitive Polynome, welche zueinander gleichwertig sind. Je nach Anwendung können weitere Auswahlkriterien hinzukommen. Beispielsweise werden in der Nachrichtentechnik im Bereich von Scramblern sogenannte dünn besetzte Generatorpolynome bevorzugt. Dies sind Polynome, welche mit einer minimalen Anzahl von Rückkoppelstellen bzw. mit einer minimalen Stellenanzahl ungleich 1 im Generatorpolynom auskommen. Dies hat den Grund, den Hardwareaufwand und bei selbstsynchronisierenden Scramblern die Vervielfachung von Empfangsfehlern im Descrambler zu minimieren. Im Bereich der Kodierungstheorie, wie bei zyklischen Kodes (CRC) oder bei kryptografischen Anwendungen, werden hingegen dichtbesetzte Polynome nach anderen Auswahlkriterien bevorzugt.

Primitive Polynome unterschiedlicher Grade sind in Tabellenwerken aufgelistet.[2][3] In nachfolgender Tabelle sind einige primitive Polynome mit minimaler Besetzung angeführt:

Grad	Exponenten	Grad	Exponenten
1	1	14	14, 13, 11, 9
2	2, 1	15	15, 14
3	3, 2	16	16, 14, 13, 11
4	4, 3	17	17, 14
5	5, 3	18	18, 11
6	6, 5	19	19, 18, 17, 14
7	7, 6	20	20, 17
8	8, 6, 5, 4	21	21, 19
9	9, 5	22	22, 21
10	10, 7	23	23, 18
11	11, 9	24	24, 23, 21, 20
12	12, 11, 8, 6	…	…
13	13, 12, 10, 6	9689	9689, 84

Programmierung

Der folgende Quelltext implementiert ein Galois-LFSR vom Grad 32 mit Periodenlänge $2^{32}-1$ :

unsigned lfsr()
{
    static unsigned r = 1;
    unsigned b = r & 1;
    r = (r >> 1) ^ (-b & 0xc3308398);
    return b;
}

Der folgende Quelltext in C++ zeigt die Implementierung eines weiteren Galois-LFSR, dessen Generatorpolynom der Benutzer selbst eingeben kann. Das Programm ermittelt die Periodenlänge des LFSR und gibt sie aus:

#include <iostream>
using namespace std;

unsigned lfsr2(unsigned _startState, unsigned _shiftBits)
{
    unsigned m = _shiftBits; m |= m >> 1; m |= m >> 2; m |= m >> 4; m |= m >> 8; m |= m >> 16;
    _startState &= m; // Entfernt überzählige Bits
    unsigned lfsr = _startState; // Initialisiert den Zustand
    unsigned periodLength = 0;
    do
    {
        unsigned lsb = lfsr & 1u; // Berechnet das Ausgabebit
        lfsr >>= 1; // Verschiebt die Zustandsbits um eine Bitposition nach rechts
        if (lsb == 1) // Wenn das Ausgabebit gleich 1 ist
        {
            lfsr ^= _shiftBits; // XOR-Rückkopplung
        }
        ++periodLength;
    } while (lfsr != _startState);
    return periodLength;
}

void main()
{
    string _startStateText;
    string _shiftBitsText;
    cin >> _startStateText; // Eingabe des Startzustands als Binärzahl über die Konsole
    cin >> _shiftBitsText; // Eingabe des Generatorpolynoms als Binärzahl über die Konsole
    unsigned _startState = stoi(_startStateText, 0, 2); // Typumwandlung von string nach unsigned
    unsigned _shiftBits = stoi(_shiftBitsText, 0, 2); // Typumwandlung von string nach unsigned
    cout << lfsr2(_startState, _shiftBits) << endl; // Ausgabe der Periodenlänge
}

Der Startzustand und das Generatorpolynom werden hier als Binärzahl über die Konsole eingegeben. Dafür ist eine Typumwandlung notwendig.

Beispiel

Für den Startzustand 1010110011100001 und das Generatorpolynom mit der Binärdarstellung 1011010000000000 ergeben sich für die ersten 6 Durchläufe der do-while-Schleife folgende Werte für das Schieberegister:

1. Durchlauf: Ergebnis nach Rechtsshift: 0101011001110000, Ausgabebit 1, Ergebnis nach XOR-Operation: 1110001001110000
2. Durchlauf: Ergebnis nach Rechtsshift: 0111000100111000, Ausgabebit 0
3. Durchlauf: Ergebnis nach Rechtsshift: 0011100010011100, Ausgabebit 0
4. Durchlauf: Ergebnis nach Rechtsshift: 0001110001001110, Ausgabebit 0
5. Durchlauf: Ergebnis nach Rechtsshift: 0000111000100111, Ausgabebit 0
6. Durchlauf: Ergebnis nach Rechtsshift: 0000011100010011, Ausgabebit 1, Ergebnis nach XOR-Operation: 1011001100010011

Anwendungen

Anwendungen von LFSRs liegen, neben den eingangs erwähnten Bereichen, bei Modulo-Zählern, welche bis zur Periodenlänge zählen und dann „überlaufen“, also wieder von vorne beginnen. Dies ist deutlich effizienter als ein arithmetischer („echter“) Zähler mit Übertragslogik (Carry-Logic), da statt einer n-Bit-Addition lediglich einige Exklusiv-Oder-Verknüpfungen (XOR) notwendig sind. Allerdings lässt sich der aktuelle Zählerstand nicht direkt aus dem Zustand des LFSR ableiten, weshalb sich ein LFSR-Zähler nur für bestimmte Anwendungen eignet, z. B. zur Index-Berechnung bei der Implementierung einer Warteschlange (First In – First Out) mittels Random-Access-Memory (RAM).

Im Bereich der digitalen Signalverarbeitung werden LFSR auch nach der Taktgeschwindigkeit in Relation zur Bitrate bzw. Symbolrate in den Anwendungen unterschieden. Bei einem Scrambler ist die Bitrate bzw. Symbolrate gleich der Taktgeschwindigkeit des LFSRs. Wird das LFSR zur spektralen Spreizung eingesetzt, ist die Taktrate des LFSR deutlich höher als die Bit- bzw. Symbolrate. Anwendung findet das etwa im Rahmen von Direct-Sequence-Spread-Spectrum-Verfahren (DSSS) bzw. – damit verwandt – im Bereich Codemultiplexverfahren (CDMA). Durch sogenannte zusammengesetzte LFSR können dann Folgen gebildet werden, wie sie beispielsweise im Rahmen von Global Positioning System (GPS) zu Navigationszwecken eingesetzt werden.

Mit linear rückgekoppelten Schieberegistern werden bei der Signaturanalyse komprimierte Bitvektoren zur Überprüfung der Funktion einer Schaltung ermittelt.

Zusammengesetzte LFSR

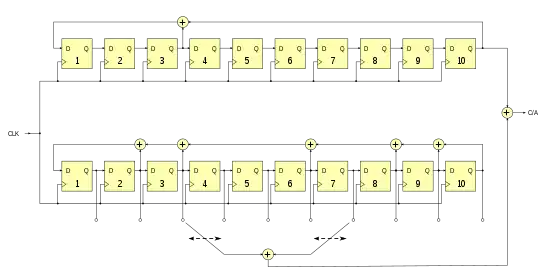
Zwei kombinierte LFSRs wie sie bei GPS zur Erzeugung der C/A-Codes (Gold-Code) Verwendung finden.

Eine Erweiterung stellt die Kombinationen der Datenfolgen verschiedenartiger LFSR dar. Die dabei entstehenden neuen Datenfolgen können andere Eigenschaften aufweisen als die ursprünglichen LFSR. Sie können damit beispielsweise durch eine geringe Autokorrelation geeigneter für Anwendungen im Bereich Code Division Multiple Access und zur spektralen Spreizung sein.

Die Zusammensetzung der Ausgabedatenfolge aus den einzelnen unabhängigen LFSRs erfolgt mittels XOR-Verknüpfung der einzelnen Teilfolgen. Weisen die LFSR unterschiedliche Folgenlängen L = 2ⁿ−1 und unterschiedliche Generatorpolynome auf, lassen sich Codefolgen mit völlig neuen Eigenschaften erzeugen. Im Regelfall weisen diese zusammengesetzten, zyklischen Folgen nicht die maximal mögliche Länge auf. Im Folgenden werden einige wichtige Klassen von aus LFSR-Registern zusammengesetzten Codefolgen dargestellt:

Gold-Folgen

Gold-Folgen wurden 1967 von Robert Gold vorgestellt und besitzen ebenfalls zwei LFSRs mit unterschiedlichen Generatorpolynomen allerdings von gleicher Länge m.[4] Die maximale Codefolgenlänge der Gold-Folge ist daher auch nur 2^m−1. Hält man den Anfangszustand eines LFSR fest und verändert den Anfangszustand („Phasenverschiebung“) des anderen zyklisch, lassen sich 2^m−1 neue Codefolgen erstellen, die alle ein relativ kleines periodisches Kreuzkorrelationsmaximum zueinander aufweisen, d. h., sie stehen fast orthogonal zueinander. Dies bedeutet, dass diese Codefolgen sich im Bereich des Codemultiplex (CDMA) verwenden lassen und damit eine Unterscheidung je nach verwendeter Gold-Folge ermöglichen.

Die Gold-Folgen sind auch wegen ihrer einfachen Erzeugung die in der Praxis am häufigsten eingesetzten Spread-Spectrum-Signale. Anwendungsbereiche liegen neben Mobilfunksystemen (UMTS), welche mit CDMA arbeiten, auch bei dem zivil nutzbaren C/A-Code des globalen Positionssystems GPS und bei WLANs.

Kasami-Folgen

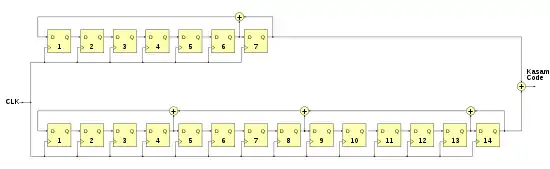
Kasami-Codegenerator wie er bei GLONASS-K Satelliten eingesetzt wird

Kasami-Folgen wurden 1966 von Tadao Kasami vorgestellt und weisen ein relativ kleines periodisches Kreuzkorrelationsmaximum zueinander auf, d. h., sie stehen fast orthogonal zueinander und werden wie die Gold-Folgen im Bereich des Codemultiplex (CDMA) eingesetzt.[5] Anwendungsbereiche dieser LFSRs liegen in Codemultiplexverfahren (CDMA) wie unter anderem im russischen Positionssystems GLONASS wo Kasami-Codefolgen ab der Satellitengeneration GLONASS-K eingesetzt werden.

Kasami-Codefolgen werden erzeugt, indem zunächst eine Maximalfolge gebildet wird, diese dezimiert wird und die so dezimierte Folge mit der Maximalfolge mittels XOR-Operation wiederholend verknüpft wird. Es gibt zwei Gruppen von Kasami-Codefolgen, die kleine und die große Gruppe. Die kleine Gruppe besteht aus zwei LFSRs, die große Gruppe wird mit drei LFSRs gebildet.

Zur Erzeugung einer Kasami-Codefolge aus der kleinen Gruppe wird ein LFSR genommen, in rechter Schaltung unten dargestellt, welches die Folge $a[n]$ mit $n=1..2^{N}-1$ erzeugt. Als Einschränkung muss $N$ gerade sein. Ein zweites LFSR, in der Darstellung darüber, erzeugt die Folge $b[n]=a[q\cdot n]$ mit dem Indexfaktor $q=2^{N/2}+1$ . Die endgültige Kasamifolge $k[n]$ wird dadurch gebildet, indem die beiden Teilfolgen miteinander XOR-verknüpft werden:

k[n]=a[n]\oplus b[n]

Die Kasami-Folge weist eine Länge von $2^{N}-1$ auf. Als Besonderheit nehmen Kasami-Folgen sowohl bei der Kreuzkorrelation als auch Autokorrelation nur folgende vier Werte an, wenn die erzeugte Codefolge mit den Elementen $\{-1,+1\}$ repräsentiert wird:

\left\{1,-{\frac {1}{N}},-{\frac {2^{N/2}-1}{N}},{\frac {2^{N/2}-1}{N}}\right\}

JPL-Folgen

JPL-Folgen bestehen aus zwei LFSRs deren Codefolgenlänge L_a und L_b teilerfremd (relativ prim) sein müssen..[6] In diesem Fall ist die Codefolgenlänge der erzeugten Gesamtfolge L_c gleich:

L_{c}=L_{a}\cdot L_{b}=(2^{n}-1)(2^{m}-1)

Es können auch mehr als zwei LFSRs mittels mehrfachen XOR am Ausgang zusammengeschaltet werden. Es müssen nur alle Codefolgelängen der einzelnen LFSR teilerfremd zueinander sein.

Entwickelt wurden JPL-Folgen in den Jet Propulsion Labs, wovon sich auch der Name für diese Codefolgen ableitet. Einsatzbereiche sind unter anderem im Bereich der Entfernungsmessung mittels Spread-Spectrum-Signalen bei Satelliten und im Bereich der Weltraumtechnik und bei dem militärisch genutzten und genaueren P/Y-Code im globalen Positionssystem GPS.

Siehe auch

Literatur

Uwe Meyer-Baese: Digital Signal Processing with Field Programmable Gate Arrays. 1. Auflage. Springer, 2001, ISBN 3-540-41341-3.

Einzelnachweise

Manfred Schroeder: Number Theory in Science and Communication. 8. Auflage. Springer, 2008, ISBN 978-3-540-85297-1.
Wayne Stahnke: Primitive Binary Polynomials. In: Mathematics of Computation. Oktober 1973, S. 977–980.
Peter Alfke: Efficient Shift Registers, LFSR Counters, and Long Pseudo-Random Sequence Generators (= Xilinx Application Note XAPP052). 1996 (online PDF).
Robert Gold: Optimal binary sequences for spread spectrum multiplexing. 4. Auflage. Volume 13. IEEE Transactions on Information Theory, S. 619–621 (online).
Tadao Kasami: Weight Distribution Formula for Some Class of Cyclic Codes (= Technical Report Nr. R-285). University of Illinois, 1966.
Alois M.J. Goiser: Handbuch der Spread-Spectrum Technik. Springer Verlag, 1998, ISBN 3-211-83080-4, Kapitel 4.3: Zusammengesetzte Folgen, S. 151 – 152.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[schroeder-1] Manfred Schroeder: Number Theory in Science and Communication. 8. Auflage. Springer, 2008, ISBN 978-3-540-85297-1.

[stahnke-2] Wayne Stahnke: Primitive Binary Polynomials. In: Mathematics of Computation. Oktober 1973, S. 977–980.

[xilinx-3] Peter Alfke: Efficient Shift Registers, LFSR Counters, and Long Pseudo-Random Sequence Generators (= Xilinx Application Note XAPP052). 1996 (online PDF).

[4] Robert Gold: Optimal binary sequences for spread spectrum multiplexing. 4. Auflage. Volume 13. IEEE Transactions on Information Theory, S. 619–621 (online).

[5] Tadao Kasami: Weight Distribution Formula for Some Class of Cyclic Codes (= Technical Report Nr. R-285). University of Illinois, 1966.

[Goiser1-6] Alois M.J. Goiser: Handbuch der Spread-Spectrum Technik. Springer Verlag, 1998, ISBN 3-211-83080-4, Kapitel 4.3: Zusammengesetzte Folgen, S. 151 – 152.