Exklusiv-Oder-Gatter

Ein Exklusiv-Oder-Gatter, auch XOR-Gatter (von englisch eXclusive OR ‚exklusives Oder‘, „entweder oder“) ist ein Gatter mit zwei Eingängen und einem Ausgang, bei dem der Ausgang logisch „1“ ist, wenn an nur einem Eingang „1“ anliegt und an dem anderen „0“. Die Exklusiv-Oder-Verknüpfung wird auch als Anti- oder Kontravalenz bezeichnet.

Gatter-Typen
	NOT
AND	NAND
OR	NOR
XOR	XNOR

Das bedeutet, dass die Eingänge verschieden beschaltet sein müssen, um am Ausgang eine „1“ zu erhalten. Entweder an dem einen oder am anderen Eingang muss „1“ anliegen. Im Unterschied zu einer einfachen OR-Verknüpfung gilt die Bedingung als nicht erfüllt, wenn an beiden Eingängen eine „1“ anliegt. Bei Exklusiv-Oder ist das Ergebnis in diesem Fall eine „0“.

Symbolik

In der Literatur wird das Exklusiv-Oder mit verschiedenen Symbolen gekennzeichnet. Üblich ist es, den Operator als „XOR“ oder „EOR“ auszuschreiben, z. B. mit dem Ausdruck „A XOR B“. Bei Verwendung des Symbols „+“ für das logische Oder wird das Symbol „ $\oplus$ “ für das Exklusiv-Oder verwendet. Bei der Verwendung von „∨“ für das logische Oder wird hingegen „⊻“ für das Exklusiv-Oder verwendet. Als bitweiser Operator findet in C (und von ihr abgeleiteten Programmiersprachen) das Zeichen ^ Verwendung.

Übersicht

Funktion

Schaltsymbol

Wahrheitstabelle

Relais-Logik

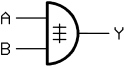
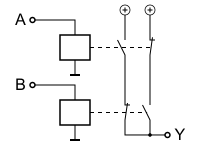
IEC 60617-12

US ANSI 91-1984

DIN 40700 (vor 1976)

Y=A\,{\underline {\lor }}\,B

Y=A\oplus B

Y=A\nleftrightarrow B

$Y=A{\overline {B}}+{\overline {A}}B$

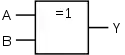oder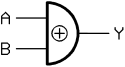

A	B	Y = A ⊻ B
0	0	0
0	1	1
1	0	1
1	1	0

Das Gleichheitszeichen = verdeutlicht beim gegenwärtig in Deutschland gültigen Schaltsymbol, dass nur bei einer „1“ an den Eingängen (High-Pegel, logisch „1“) der Ausgang „1“ ist.

Synthese

Exklusiv-Oder

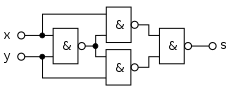
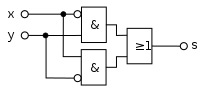
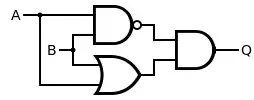
Aufbau eines Exklusiv-Oder-Gatters aus vier NAND-Gattern	Aufbau eines Exklusiv-Oder-Gatters aus Und-, Oder- und Nicht-Gattern (letztere für die Negation je eines der Und-Gatter-Eingänge)	Aufbau eines Exklusiv-Oder-Gatters aus Und-, Oder- und NAND-Gattern

Die linke Abbildung zeigt den Aufbau eines Exklusiv-Oder-Gatters aus vier NAND-Bausteinen gemäß der logischen Antivalenz

x\,{\underline {\lor }}\,y\Leftrightarrow {\Big (}x\,{\overline {\land }}\,(x\,{\overline {\land }}\,y){\Big )}\,{\overline {\land }}\,{\Big (}y\,{\overline {\land }}\,(x\,{\overline {\land }}\,y){\Big )}

Die mittlere Abbildung zeigt den Aufbau eines Exklusiv-Oder-Gatters aus Nicht-, Und- und Oder-Bausteinen. Aufgrund der Vielzahl an unterschiedlichen Komponenten besteht allerdings nur in Ausnahmefällen Relevanz für die Umsetzung in Hardware:

x\,{\underline {\lor }}\,y\Leftrightarrow {\Big (}\,(\neg {x}\land y)\lor (x\land \neg {y})\,{\Big )}

Die rechte Abbildung zeigt den Aufbau eines Exklusiv-Oder-Gatters aus einem NAND-, einem Und- und einem Oder-Gatter.

x\,{\underline {\lor }}\,y\Leftrightarrow {\Big (}\,(x{\overline {\land }}y)\land (x\lor y)\,{\Big )}

Programmierung

Die Exklusiv-Oder-Verknüpfung lässt sich auch durch die Addition zweier Bits modulo 2 berechnen. Dazu berechnet man die einfache Summe der Eingangssignale, dividiert die Summe durch 2 und betrachtet danach den Rest der Division. Ist die Summe eine gerade Zahl, so ist der Rest gleich null, ist sie ungerade, so ist der Rest gleich eins. Weiterhin kann die einfache Exklusiv-Oder-Verknüpfung zweier Eingangssignale auch als Anzeige der Ungleichheit der Eingangsbits angesehen werden. Dieses gilt auch für eine beliebige gerade Anzahl an Eingangssignalen.

Anwendung

Addition von binären Zahlen

Ein Exklusiv-Oder-Gatter kann zur Addition von binären Zahlen eingesetzt werden. Hier wird zusätzlich, zum Beispiel mit Hilfe eines Und-Gatters, beim Zustand x=1 und y=1 ein sogenannter Übertrag gebildet. Dieser Übertrag ist bei der Addition des nächsthöheren Bits als „1“ zu berücksichtigen. Der Addierer des Von-Neumann-Addierwerks benutzt diese Logik.

Kryptografie

Das nachweislich sichere Verschlüsselungsverfahren One-Time-Pad wird meist unter Zuhilfenahme einer Exklusiv-Oder-Verknüpfung implementiert. Die zu verschlüsselnde Nachricht (Klartext) wird dazu zuerst als Bitfolge kodiert. Eine zweite zufällige Bitfolge, die genauso lang wie die Nachricht ist, wird als Schlüssel verwendet. Der Geheimtext entsteht, indem das erste Bit der Nachricht mit dem ersten Bit des Schlüssels exklusiv-oder-verknüpft wird, das zweite Bit mit dem zweiten und so weiter. Führt man anschließend die gleiche Exklusiv-Oder-Verknüpfung mit dem Geheimtext und dem Schlüssel aus, so erhält man wieder die ursprüngliche Nachricht.

Sicherheit

Fällt einem Angreifer der Klartext und der Geheimtext in die Hand, kann er sehr einfach mittels Exklusiv-Oder-Verknüpfung den Schlüssel herausfinden, und diesen bei weiteren Geheimtexten ausprobieren. Die Gewinnung des Schlüssels ist bei anderen Methoden (z. B. AES) kaum möglich. Das spielt beim One-Time-Pad-Verfahren allerdings keine Rolle, da für jede Nachricht voneinander vollständig unabhängige Schlüssel verwendet werden.
Angriff auf exklusiv-oder-verschlüsselte Daten, falls die Schlüssellänge kürzer ist als der Geheimtext:[1]
- Mit Exklusiv-Oder-Operationen wird der Geheimtext mit Geheimtext_n verarbeitet, wobei Geheimtext_n dem um n Bits nach rechts verschobenen Geheimtext entspricht. Wie viele Bits bleiben nach der Exklusiv-Oder-Operation jeweils dieselben? Die Schlüssellänge entspricht der Verschiebung n, bei der das Resultat von Geheimtext XOR Geheimtext_n am stärksten dem Geheimtext ähnelt.
- Nun ist die Schlüssellänge n gefunden. Die Operation Geheimtext XOR Geheimtext_n ergibt dasselbe Resultat wie Klartext XOR Klartext_n. Denn es gilt:[2]

Geheimtext\oplus Geheimtext_{n}=(Klartext\oplus Schluessel)\oplus (Klartext_{n}\oplus Schluessel)=(Klartext\oplus Schluessel)\oplus (Schluessel\oplus Klartext_{n})

=Klartext\oplus (Schluessel\oplus Schluessel)\oplus Klartext_{n}=Klartext\oplus Klartext_{n}

Es fällt in der Regel genügend Klartext an, um die Nachricht vollends zu entziffern. Denn es gilt:[2]

Klartext\oplus Klartext_{n}\oplus Klartext_{n}=Klartext

Weitaus einfacher gestaltet sich die Entschlüsselung, wenn der Schlüssel n Bits lang ist und im Klartext die gleichen Bits sich m Mal wiederholen, wobei m ein Vielfaches von n darstellt. Hier als Beispiel eine Wiederholung von Nullen; der Schlüssel ist 1010. Da sich im verschlüsselten Text die Sequenz 1010 wiederholt, kann der Angreifer vermuten, dass der Klartext an dieser Stelle aus Nullen bestand und der Schlüssel 1010 war (oder der Geheimtext aus Einsen, und der Schlüssel war 0101):

Klartext XOR Schlüssel → Geheimtext
11111001000000000000 XOR 10101010101010101010 → 01010011101010101010

Die Exklusiv-Oder-Verschlüsselung lässt sich aber entscheidend verbessern, indem aus einem kurzen Passwort ein genügend langer Schlüssel erzeugt wird. Ein Beispiel dafür ist die Verschlüsselung mittels RC4, die aber mittlerweile als unsicher gilt. Sicherer, aber etwas langsamer ist die Verschlüsselung mit Spritz.

Prüfsummenbildung

XOR 1011 = 1110

XOR 1110 = 0101

XOR 1110 = 1011

Aus zwei Bitfolgen, angenommen 0101 und 1011, wird mittels der Exklusiv-Oder-Verknüpfung die Parität gebildet: 1110 (erste Zeile im Beispiel rechts). Diese Parität muss zusammen mit den beiden Bitfolgen übertragen bzw. gespeichert werden. Geht nun die erste Bitfolge (0101) verloren, so kann sie wiederhergestellt werden, indem die zweite Bitfolge (1011) mit der Parität exklusiv-oder-verknüpft wird (zweite Zeile). Analog könnte die zweite Bitfolge wiederhergestellt werden (dritte Zeile). Dieser Mechanismus wird unter anderem auch bei RAID 5 verwendet: Je zwei Datenblöcke (aus z. B. 512 Bytes) werden auf je eine Festplatte geschrieben. Auf eine dritte Platte wird die XOR-Verknüpfung der beiden ersten Blöcke geschrieben. Geht jetzt irgendeine der drei Festplatten kaputt, kann die Information vollständig aus den beiden anderen restauriert werden.

Frequenzverdopplung

Frequenzverdopplung eines Rechtecksignals

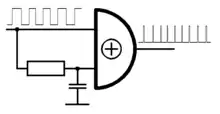
Eine sehr einfache Frequenzverdopplung von Rechteckschwingungen im Frequenzbereich bis zu einigen 100 MHz kann mit einem Exklusiv-Oder-Gatter erzielt werden, wenn ein Eingang unmittelbar und der andere mit einem geringfügig verzögerten Signal (in der Zeichnung durch ein RC-Glied dargestellt, denkbar sind aber auch Schaltungen beispielsweise mit Gatterlaufzeiten, wie etwa zwei Inverter) gespeist wird. Das Exklusiv-Oder-Gatter schaltet bei steigender und fallender Flanke; die entstehenden Nadelimpulse sind phasengebunden und etwa so kurz wie die eingesetzte Signalverzögerung. Da dieses Verfahren keine Resonanzfilter verwendet, kann das Eingangssignal fast beliebige Tastverhältnisse besitzen bzw. stark frequenzmoduliert sein, allerdings ist im Allgemeinen kein Tastgrad von 50 % zu erreichen.

Schaltbarer Inverter

An einem Eingang liegt ein Signal an, der andere dient als Steuereingang. Liegt der Steuereingang auf logisch „0“, wird das Signal ohne Änderung durchgelassen. Liegt der Steuereingang auf logisch „1“, verhält sich das Gatter wie ein Inverter.

CMOS-Realisierung

Schaltbild in CMOS-Technik

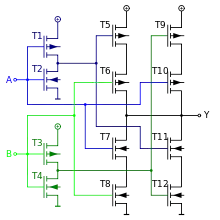
Die zuvor gezeigte Realisierung aus Und- und Oder-Gattern benötigt in CMOS-Technik 16 Transistoren. Eine direkte Umsetzung (rechts) benötigt nur 12 Transistoren und mit Tricks, unter Einbußen bei der Geschwindigkeit, sechs Transistoren bzw. vier Transistoren. Zum Verständnis: T1+T2 und T3+T4 invertieren die Eingangssignale. Bei High-Potential an beiden Eingängen (A+B) leiten T7+T8 und ziehen den Ausgang Y auf Low-Potential. Sind beide Eingänge auf Low-Potential, leiten T11+T12, da vor beiden ein Inverter liegt, der das Eingangssignal umkehrt.

Weiterhin gibt es Implementierungen, die sowohl XOR wie NXOR als Ergebnis zur Verfügung stellen.

Ein so optimierter Voll-Addierer benötigt nur noch 26 Transistoren (2 × 4 Transistoren für das Exklusiv-Oder der Summe, 3 × 4 Transistoren für das 2-fach-NAND und 1 × 6 Transistoren für das 3-fach-NAND für den Übertrag). Ein 64 × 64-bit-Multiplizierer lässt sich so als Schaltnetz mit knapp 140.000 Transistoren implementieren.

Literatur

Ulrich Tietze, Christoph Schenk: Halbleiter-Schaltungstechnik. 12. Auflage. Springer, 2002, ISBN 3-540-42849-6.
Klaus Beuth: Digitaltechnik. 10. Auflage. Vogel, 1998, ISBN 3-8023-1755-6.
Manfred Seifart, Helmut Beikirch: Digitale Schaltungen. 5. Auflage. Technik, 1998, ISBN 3-341-01198-6.

Einzelnachweise

Bruce Schneier: Angewandte Kryptographie. 2006.
Jürgen Schmidt: KRACK – so funktioniert der Angriff auf WPA2. In: heise Security. Heise Medien GmbH & Co. KG, 19. Oktober 2017, abgerufen am 24. Oktober 2017.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Bruce Schneier: Angewandte Kryptographie. 2006.

[KRACK-2] Jürgen Schmidt: KRACK – so funktioniert der Angriff auf WPA2. In: heise Security. Heise Medien GmbH & Co. KG, 19. Oktober 2017, abgerufen am 24. Oktober 2017.