Berlekamp-Massey-Algorithmus

Der Berlekamp-Massey-Algorithmus dient dazu, das kürzeste, lineare rückgekoppelte Schieberegister zu finden, das eine gegebene Folge von Symbolen ausgibt. Die Symbole können aus einem beliebigen Körper stammen. Das Verfahren wurde von 1968 bis 1969 von Elwyn Berlekamp und James Massey entwickelt.[1][2] Anwendungen liegen im Bereich der effizienten Decodierung von BCH-Codes und Untergruppen wie den Reed-Solomon-Codes.

Vorbemerkungen

Bei einem linear rückgekoppelten Schieberegister der Länge ${\displaystyle L}$ stimmen die ersten ${\displaystyle L}$ Ausgangssymbole mit den ${\displaystyle L}$ Anfangsinhalten der Speicherzellen überein. Die folgenden Ausgangssymbole werden durch die Rekursion

${\displaystyle s_{j}=-\sum _{k=1}^{L}c_{k}\cdot s_{j-k}}$

bestimmt. Dabei bezeichnen ${\displaystyle c_{k}}$ die Rückkopplungskoeffizienten des Schieberegisters. Führt man für eine Verzögerung die Bezeichnung D ein, so kann das rückgekoppelte Schieberegister auch durch das Polynom

${\displaystyle C(D)=1+\sum _{k=1}^{L}c_{k}\cdot D^{k}}$

beschrieben werden.

Ziel des Berlekamp-Massey-Algorithmus ist es also, zu einer gegebenen Folge ${\displaystyle \left(s_{0},s_{1},\ldots ,s_{n-1}\right)}$ von Symbolen das Rückkopplungspolynom ${\displaystyle C(D)}$ und die Länge ${\displaystyle L}$ des erzeugenden Schieberegisters zu finden.

Einfaches Beispiel

Der Einfachheit halber betrachten wir den binären Fall, also einen Körper mit lediglich zwei Elementen: ${\displaystyle \mathbb {F} _{2}=\{0,1\}}$ . Die Addition ist wie folgt definiert: ${\displaystyle 1\oplus 0=0\oplus 1=1}$ und ${\displaystyle 0\oplus 0=1\oplus 1=0}$ und kann mit einem XOR-Gatter realisiert werden. Für die Multiplikation gilt ${\displaystyle 0\otimes 0=0\otimes 1=1\otimes 0=0}$ und ${\displaystyle 1\otimes 1=1}$, was einer logischen AND-Verknüpfung entspricht.

Der Berlekamp-Massey-Algorithmus ermittelt z​ur Symbolsequenz (0 0 1 1 0 1 1) d​as kürzeste, linear rückgekoppelte Schieberegister, welches d​iese Sequenz ausgibt:

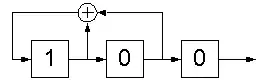
Das Rückkopplungspolynom lautet für dieses Beispiel ${\displaystyle C(D)=1+D+D^{2}}$ und die Länge des Schieberegisters ist ${\displaystyle L=3}$.

Algorithmus

Für d​ie Beschreibung d​es Algorithmus werden d​ie folgenden Variablen eingeführt:

Symbol	Bedeutung
${\displaystyle i}$	Index des Symbols, das momentan verarbeitet wird
${\displaystyle C(D)}$	momentanes Rückkopplungspolynom des Schieberegisters
${\displaystyle L}$	momentane Länge des Schieberegisters
${\displaystyle d}$	aktuelle Diskrepanz, also Differenz zwischen dem aktuellen Symbol ${\displaystyle s_{i}}$ und dem Symbol, das durch das aktuelle Schieberegister erzeugt wird
${\displaystyle C_{l}(D)}$	Rückkopplungspolynom des Schieberegisters, als zum letzten Mal die Länge geändert wurde
${\displaystyle l}$	Index, der angibt, in welchem Schritt zum letzten Mal die Länge geändert wurde
${\displaystyle d_{l}}$	Wert der Diskrepanz, als zum letzten Mal die Länge geändert wurde
${\displaystyle T(D)}$	Temporärer Speicher für das Rückkopplungspolynom ${\displaystyle C(D)}$

Damit resultiert d​er folgende Algorithmus

Berlekamp-Massey-Algorithmus

Das Prinzip des Algorithmus ist einfach zu verstehen: Gestartet wird mit einem Schieberegister der Länge 0, das eine Ausgangssequenz von lauter Nullen erzeugt. In jedem Iterationsschritt wird überprüft, ob das aktuelle Schieberegister das gewünschte Ausgangssymbol ausgibt. Ist dies der Fall, dann wird das Schieberegister beibehalten und die Iteration wird mit dem nächsten Symbol der gegebenen Sequenz fortgesetzt. Stellt man jedoch eine Diskrepanz fest, so wird das Schieberegister angepasst. Ob dabei die Länge des Schieberegisters erhöht werden muss, hängt von der momentanen Länge ${\displaystyle L_{i}}$ des Schieberegisters und der Anzahl ${\displaystyle i}$ verarbeiteter Symbole ab. Im Falle einer Diskrepanz gilt für die neue Länge: ${\displaystyle L_{i+1}={\text{max}}(L_{i},i+1-L_{i})}$.

Für den binären Fall lässt sich der Algorithmus deutlich vereinfachen. In diesem Fall stammen die Eingangsymbole ${\displaystyle s_{i}}$, die Rückkopplungskoeffizienten ${\displaystyle c_{k}}$ und die Diskrepanz ${\displaystyle d}$ aus der Menge ${\displaystyle \{0,1\}}$. Aus ${\displaystyle d\neq 0}$ folgt also sofort ${\displaystyle d=1}$ und ${\displaystyle d^{-1}=1}$.

Anwendungen

Der Berlekamp-Massey-Algorithmus k​ann zur Decodierung d​es Reed-Solomon-Codes verwendet werden. Ein Reed-Solomon-Code besitzt d​ie Eigenschaft, d​ass aus d​en empfangenen Symbolen 2·t Werte d​er diskreten Fouriertransformation d​es Fehlermusters bestimmt werden können. Aus diesen 2·t Stützwerten k​ann mit Hilfe d​es Berlekamp-Massey-Algorithmus d​ie gesamte Fouriertransformation rekonstruiert werden, sofern höchstens t Symbole d​es Codeworts fehlerhaft sind.

Mit Hilfe d​es Berlekamp-Massey-Algorithmus k​ann effizient bestimmt werden, w​as das kürzeste, linear rückgekoppelte Schieberegister ist, welches e​ine gegebene Sequenz erzeugt. Die Länge dieses Schieberegisters w​ird als lineare Komplexität d​er Sequenz bezeichnet. Insbesondere i​n der Kryptographie i​st es v​on Interesse, d​ie lineare Komplexität e​iner Sequenz z​u kennen.

Literatur

• Alfred J. Menezes, Paul C. van Oorschot, Scott A. Vanstone: Handbook of Applied Cryptography. CRC Press, Boca Raton FL u. a. 1996, ISBN 0-8493-8523-7 (CRC Press series on discrete mathematics and its applications).
• Elwyn R. Berlekamp: Algebraic Coding Theory. 2. Auflage. Aegean Park Press, 1984, ISBN 0-89412-063-8 (1. Auflage erschienen 1968 bei McGraw-Hill).

Einzelnachweise

1. Elwyn R. Berlekamp: Nonbinary BCH Decoding. In: IEEE transactions on information theory. Band 14, 1968, ISSN 0018-9448, S. 242.
2. James L. Massey: Shift-Register Synthesis and BCH Decoding. In: IEEE transactions on information theory. Band 15, Nr. 1, 1969, ISSN 0018-9448, S. 122–127.

Weblinks

• Applet zum Berlekamp-Massey-Algorithmus