Hebel (Physik)

Ein Hebel ist in der Physik und Technik ein mechanischer Kraftwandler bestehend aus einem starren Körper, der um einen Drehpunkt drehbar ist. Die mathematische Beschreibung eines solchen Systems im (Drehmoment-)Gleichgewicht wird als Hebelgesetz bezeichnet. Dieses Gesetz wurde bereits in der Antike durch Archimedes formuliert.

Hebel in physikalischer Beschreibung

Hebel in technischer Beschreibung

Veranschaulichung des Hebelgesetzes: Das 20-fache Gewicht wird bei 20-fachem Hebelarm im Gleichgewicht gehalten (wenn man das Gewicht des asymmetrischen Hebelarms nicht in Betracht zieht).

Kinderspielplatz: Eine Wippe ist ein Hebel

Nussknacker: Beispiel für einen einseitigen Doppelhebel

Hebel zur Pumpenbetätigung in der Alten Saline in Bad Reichenhall

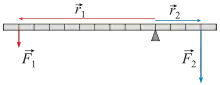
Unterschieden werden einseitige und zweiseitige Hebel, je nachdem ob die Kräfte nur auf einer Seite oder auf beiden Seiten des Drehpunktes angreifen.[1] Weiter gibt es neben dem geraden Hebel auch noch den geknickten Hebel oder Winkelhebel,[2] wie er in der Neigungswaage Anwendung findet.

Physikalische Beschreibung

Die zentrale physikalische Größe, die zur Beschreibung eines Hebels benötigt wird, ist das Drehmoment ${\vec {M}}$ in Bezug auf den Drehpunkt $A$ , um den sich der Hebel drehen kann.

{\vec {M}}={\vec {r}}_{\text{A}}\times {\vec {F}}

Dabei ist ${\vec {r}}_{\text{A}}$ der Vektor vom Drehpunkt $A$ auf den Punkt, an dem die Kraft ${\vec {F}}$ angreift. Der senkrechte Abstand zwischen der Wirkungslinie der Kraft und dem Bezugspunkt wird Hebelarm $h$ genannt.[3] Seine Länge lässt sich berechnen durch

h=|{\vec {r_{\text{A}}}}|\cdot \sin \alpha

mit dem Winkel $\alpha$ zwischen dem Vektor ${\vec {r}}_{\text{A}}$ und der Wirkungslinie der Kraft.[4]

Der Betrag des Drehmoments ist proportional zum Hebelarm. Mit einem großen Hebelarm kann daher mit einer kleinen Kraft ein großes Drehmoment ausgeübt werden. Dieser Umstand veranlasste Archimedes zu der Bemerkung:

„Gebt mir einen festen Punkt im All, und ich werde die Welt aus den Angeln heben.“[5]

Ein Hebel befindet sich im Gleichgewicht, wenn die Summe aller an ihm anliegenden Drehmomente bezüglich desselben Bezugspunktes (nicht notwendigerweise der Drehpunkt) gleich Null ist:

\sum _{n=0}^{N}{\vec {M}}_{n}=\sum _{n=0}^{N}{\vec {r}}_{n}\times {\vec {F}}_{n}=0

Wird der Hebel durch Störung des Gleichgewichts durch ein weiteres Drehmoment gekippt, so wird auf beiden Seiten des Drehpunktes die gleiche Arbeit $W={\vec {F}}_{1}\cdot {\vec {s}}_{1}={\vec {F}}_{2}\cdot {\vec {s}}_{2}$ verrichtet, wobei ${\vec {s}}_{1,2}$ jeweils der Weg ist, der bei der Kippbewegung zurückgelegt wird.

Die Rechnung vereinfacht sich, wenn man Kräfte betrachtet, die senkrecht zum Hebel stehen. Dadurch wird das Kreuzprodukt zu einem normalen Produkt der Beträge der Vektoren. Es ergibt sich das Verhältnis

\left|{\vec {r}}_{1}\right|\left|{\vec {F}}_{1}\right|=\left|{\vec {r}}_{2}\right|\,\left|{\vec {F}}_{2}\right|

der beiden Kräfte ${\vec {F}}_{1}$ und ${\vec {F}}_{2}$ an den Punkten ${\vec {r}}_{1}$ und ${\vec {r}}_{2}$ des Hebels.

Eine weitere Größe, die betrachtet werden kann, ist die Geschwindigkeit an verschiedenen Stellen des Hebels während der Bewegung des Hebels. Da es sich um eine Rotationsbewegung handelt, hängt die Bahngeschwindigkeit $v={\dot {s}}$ vom Abstand $r=\left|{\vec {r}}\right|$ zum Drehpunkt und von der Winkelgeschwindigkeit ${\dot {\varphi }}$ ab: $v=r{\dot {\varphi }}$ . Aus dieser Überlegung kann, analog zum Kraftverhältnis, eine Gleichung zur Berechnung des Geschwindigkeitsverhältnisses aufgestellt werden:

{\frac {r_{1}}{r_{2}}}={\frac {v_{1}}{v_{2}}}

Reale Hebel

Waage (hier Balkenwaage): Nutzung des Hebelgesetzes zur Bestimmung des Wägewerts

Rudern: Viel Kraft und langer Lastarm führen zu hoher Geschwindigkeit

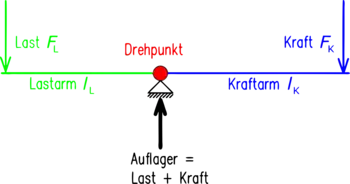
In der Technik werden Hebel durch ihre drei Komponenten beschrieben:

Lastarm: Hebelarm auf der Seite der zu bewegenden Last
Kraftarm: Hebelarm auf der Seite der bewegenden Kraft
Angelpunkt bzw. Drehpunkt: Punkt, um den sich der Hebel drehen kann

Mit diesen Bezeichnungen lautet das Hebelgesetz:

„Kraft mal Kraftarm ist gleich Last mal Lastarm“

Bei einem einseitigen Hebel liegen Lastarm und Hebelarm auf derselben Seite, da der Drehpunkt sich an einem Ende des Hebels befindet, jedoch haben beide eine unterschiedliche Länge. Bei realen Hebeln ist die Wirkung der Reibung im Drehpunkt nicht zu vernachlässigen. Dadurch ist eine höhere bewegende Kraft nötig bzw. die resultierende Kraft erreicht nicht den theoretischen Wert, da ein Teil der verrichteten Arbeit in Wärme umgewandelt wird. Ein weiteres technisches Problem ist die Verformbarkeit von realen Materialien: In der Natur existieren keine „perfekt starren“ Körper. Das führt dazu, dass der Hebel am Drehpunkt verbiegt oder bricht und nicht die gewünschte Kraft auf die Last überträgt. Um diese Effekte zu verringern, werden als Drehpunkt z. B. Kugeln oder Rollen eingesetzt, um zu starkes Abknicken zu verhindern.

Reale Hebel, wie sie z. B. im Maschinenbau verwendet werden, können aus verschiedensten Werkstoffen bestehen. Im klassischen Maschinenbau bestehen Hebel aus Gusseisen oder Stahl, wobei die am stärksten belasteten Hebel in der Regel bei der Herstellung geschmiedet werden. In anderen industriellen Bereichen werden auch Hebel aus anderen Materialien, wie z. B. Kunststoffen, verwendet.

Anwendungen

Hebel finden sich in vielen technischen und alltäglichen Dingen wieder. Beim Rudern findet das Hebelgesetz Anwendung, indem die Sportler durch eine große Kraft am kurzen Ende einen weiten Weg am langen Ende des Ruders zurücklegen, was zu einer großen Geschwindigkeit führt. Auch wenn es auf den ersten Blick anders erscheint: Das Ruder ist ein einseitiger Hebel. Last und Kraft greifen auf der gleichen Seite an. Der Drehpunkt, hier auch Stützpunkt genannt (der Punkt, an dem sich der Hebel abstützt), liegt am Ruderblatt. Weil die Bewegung des Bootes der eigentliche Zweck ist, kann das eingetauchte Ruderblatt als Drehpunkt betrachtet werden, um den sich das Boot bewegt, also in die Wirkrichtung der angreifenden Kraft geschoben wird. Das Ruder ist an der sogenannten Dolle am Boot befestigt; sie ist lediglich der Angriffspunkt der Last, nicht der Drehpunkt des Hebels. Die genaue Lage des Drehpunktes hängt davon ab, wie stark das Ruder im Verhältnis zum Boot verankert ist: Stützt sich das Ruderblatt von einem Felsen ab, liegt dort der Drehpunkt; beim Rudern in der Luft ist die Dolle der Drehpunkt.

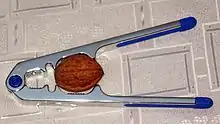
Auf Kinderspielplätzen finden sich Hebel in Form von Wippen. Dort wird die Wippe durch wechselseitiges Anlegen einer Kraft hin- und hergeschwenkt. Ein Nussknacker ist ein einseitiger Doppelhebel.[6] Balkenwaagen nutzen das Hebelgesetz, um Gewichte zu vergleichen. In der Fahrzeugtechnik werden Kipphebel verwendet, um die Richtung einer Kraft zu ändern. Nageleisen nutzen das Gesetz, um mit wenig Handkraft auf einem langen Weg Nägel aus Holz zu ziehen. In der Klaviermechanik ist besonders das Geschwindigkeitsverhältnis von Bedeutung. Ein weiterer Anwendungsfall ist der Kniehebel, beispielsweise bei der Kniehebelpresse.

Eine Zange verstärkt die Handkraft und kann je nach Konstruktion ein Werkstück pressend halten oder aufweiten (etwa einen Seegerring, ein Bleirohr). Ein Bolzenschneider weist eine doppelte Hebeluntersetzung auf, um hohe Schnittkraft zu erreichen, die langen Bedienhebel werden mit beiden Armen auf relativ langem Weg kräftig zusammengedrückt. Eine schließende Pinzette bietet federnde Haltekraft, die kleiner ist als die Fingerkraft. Schaufel und Brechstange können an der Front hohe Kräfte ausüben, weil die Armkraft an einem langen Stiel ansetzt.

Weblinks

Commons: Hebel – Sammlung von Bildern, Videos und Audiodateien

Commons: Piano-Hebelmechanik – Sammlung von Bildern, Videos und Audiodateien

Animierte, interaktive Veranschaulichung zum Hebelgesetz von Walter Fendt
Veranschaulichung, Aufgaben und Erläuterungen zum zweiseitigen Hebel auf LEIFIphysik
Aufgaben und Erläuterungen zum einseitigen Hebel auf LEIFIphysik

Einzelnachweise

Heinz Gascha, Stefan Franz: Großes Handbuch Physik. Compact, 2004, ISBN 3-8174-7429-6, S. 33.
Horst Stöcker: Taschenbuch der Physik. 6. Auflage. Harri Deutsch, 2010, ISBN 978-3-8171-1860-1, S. 95.
Alfred Böge (Hrsg.): Handbuch Maschinenbau: "Das Moment einer Einzelkraft F in Bezug auf einen gewählten Drehpunkt D ist festgesetzt (definiert) als das Produkt aus der Kraft und deren Wirkabstand l (Lot von der Wirklinie auf den gewählten Drehpunkt D)[…] Wirkabstand l heißt auch „Hebelarm“."
Skolaut: Maschinenbau: "Der Hebelarm einer Kraft ist definiert als der Abstand der Kraftwirkungslinie zum betrachteten Momentenbezugspunkt"
Dankert: Technische Mechanik: "Der Hebelarm ist die kürzeste Verbindung vom Bezugspunkt bis zur Wirkungslinie der Kraft"
Stefan Hartmann: Technische Mechanik. Wiley-VCH, 2015, S. 41.
Zitiert von Pappos in Sammlungen, Buch VIII
R. Brinkmann: Hebel. (Memento vom 23. Juni 2011 im Internet Archive)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Heinz Gascha, Stefan Franz: Großes Handbuch Physik. Compact, 2004, ISBN 3-8174-7429-6, S. 33.

[2] Horst Stöcker: Taschenbuch der Physik. 6. Auflage. Harri Deutsch, 2010, ISBN 978-3-8171-1860-1, S. 95.

[3] Alfred Böge (Hrsg.): Handbuch Maschinenbau: "Das Moment einer Einzelkraft F in Bezug auf einen gewählten Drehpunkt D ist festgesetzt (definiert) als das Produkt aus der Kraft und deren Wirkabstand l (Lot von der Wirklinie auf den gewählten Drehpunkt D)[…] Wirkabstand l heißt auch „Hebelarm“."
Skolaut: Maschinenbau: "Der Hebelarm einer Kraft ist definiert als der Abstand der Kraftwirkungslinie zum betrachteten Momentenbezugspunkt"
Dankert: Technische Mechanik: "Der Hebelarm ist die kürzeste Verbindung vom Bezugspunkt bis zur Wirkungslinie der Kraft"

[4] Stefan Hartmann: Technische Mechanik. Wiley-VCH, 2015, S. 41.

[5] Zitiert von Pappos in Sammlungen, Buch VIII

[6] R. Brinkmann: Hebel. (Memento vom 23. Juni 2011 im Internet Archive)