Binomial-Heap

In der Informatik ist ein Binomial-Heap eine Datenstruktur, genauer ein Heap, der sich, ähnlich wie binäre Heaps, als Vorrangwarteschlange einsetzen lässt. Das heißt, dass in beliebiger Reihenfolge effizient Elemente mit festgelegter Priorität in den Heap hineingelegt werden können und stets das Element mit höchster Priorität entnommen werden kann.

Im Unterschied zu binären Heaps können Binomial-Heaps auch effizient vereinigt werden. Dies ermöglicht es beispielsweise, effizient in einem Mehrprozessor-Multitasking-System die Aufgaben eines überlasteten Prozessors einem anderen zu übertragen.

Die Priorität der Elemente wird diesen durch Schlüssel aufgeprägt. Über der Menge der Schlüssel muss daher eine totale Ordnung bestehen, wie sie zum Beispiel die Kleiner-Gleich-Relation (≤) über den ganzen Zahlen darstellt.

Binomial-Heaps wurden erstmals 1978 von Jean Vuillemin beschrieben. 1987 wurde von Michael L. Fredman und Robert Tarjan daraus eine neue Datenstruktur abgeleitet, die sogenannten Fibonacci-Heaps. Diese besitzen amortisiert teilweise bessere Laufzeiten und finden unter anderem Anwendung im Algorithmus von Dijkstra und im Algorithmus von Prim. Ihre Worst-Case Laufzeit ist teilweise aber deutlich schlechter, weshalb sie sich nicht für Online-Algorithmen eignen.

Operationen

Binomial-Heaps unterstützen effizient die Operationen

insert – zum Einfügen eines Elementes,
remove – zum Entfernen eines Elementes,
extractMin – zur Rückgabe und zum Entfernen eines Elementes mit minimalem Schlüssel (=höchster Priorität),
changeKey – zum Ändern des Schlüssels eines Elementes und
merge – zum Verschmelzen zweier Heaps.

Alle Operationen lassen sich mit einer Worst-Case-Laufzeit von O(log n) implementieren, wobei n die Zahl der aktuell im Heap befindlichen Elemente ist.

Binomial-Bäume

Binomial-Baum der Ordnung 3

Binomial-Heaps bestehen aus einer Liste von Binomial-Bäumen verschiedener Ordnung. Binomial-Bäume und ihre Ordnung sind dabei wie folgt rekursiv definiert:

Ein Binomial-Baum der Ordnung 0 besteht aus einem einzelnen Knoten.
Ein Binomial-Baum der Ordnung k besitzt eine Wurzel mit Grad k, deren Kinder genau die Ordnung k−1, k−2, ..., 0 (in dieser Reihenfolge) besitzen.

Ein Binomial-Baum der Ordnung k lässt sich also auch leicht aus zwei Binomial-Bäumen der Ordnung k−1 erstellen, indem einer der beiden Bäume zum am weitesten links stehenden Kind des anderen gemacht wird. Aus dieser Konstruktion lässt sich leicht per vollständiger Induktion die Eigenschaft ableiten, dass ein Binomial-Baum der Ordnung k genau 2^k Knoten und die Höhe k besitzt.

Struktur eines Binomial-Heaps

Ein Binomial-Heap speichert seine Elemente und die zugehörigen Schlüssel in den Knoten seiner Binomial-Bäume. Dabei erfüllt er folgende Eigenschaften:

Jeder Binomial-Baum im Heap erfüllt die Heap-Bedingung, das heißt mit Ausnahme der Wurzel, die keinen Elternknoten besitzt, gilt für jeden seiner Knoten, dass der zugehörige Schlüssel größer oder gleich dem Schlüssel seines Elternknotens ist.
Für jede natürliche Zahl k existiert höchstens ein Binomial-Baum der Ordnung k.

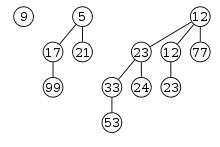
Beispiel eines Binomial-Heaps mit 13 Elementen. Die Schlüssel der Väter sind höchstens so groß wie die Schlüssel ihrer Kinder.

Die erste Eigenschaft gewährleistet, dass die Wurzel jedes Baumes ein Element mit kleinstem Schlüssel im Baum trägt. Zusammen mit der Eigenschaft, dass ein Binomial-Baum der Ordnung k genau 2^k Knoten besitzt, stellt die zweite Eigenschaft sicher, dass für einen Binomial-Heap mit n Elementen exakt festgelegt ist, wie viele Bäume der Heap besitzt und welche Ordnung diese besitzen.

Dies ist durch die Binärdarstellung von n festgelegt. Werden die Ziffern von rechts nach links mit 0 beginnend durchnummeriert, so existiert ein Baum der Ordnung k genau dann, wenn in der Binärdarstellung an der Stelle k eine 1 steht. Dies bedeutet auch, dass ein Heap mit n Elementen höchstens log₂(n+1) Binomial-Bäume enthält. Ein Binomial-Heap mit 13=1101₂ Elementen besitzt beispielsweise genau einen Baum der Ordnung 3, einen Baum der Ordnung 2 und einen Baum der Ordnung 0.

Die Menge der Binomial-Bäume wird als (nach der Ordnung der Bäume) sortierte Liste der Wurzeln dieser Bäume implementiert. Ein Binomial-Heap besitzt im Gegensatz zum Binär-Heap nicht eine einzige Wurzel, sondern mehrere. Diese werden als Wurzelliste bezeichnet. Dadurch erhöht sich die Laufzeit für das Finden des Minimums auf O(log n), da alle Elemente der Wurzelliste durchsucht werden müssen.

Implementierung der Operationen

Verschmelzen zweier Heaps (merge)

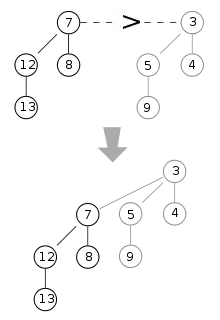
Verschmelzen zweier Binomialbäume von Grad 2: Vergleiche die Wurzeln und füge dem Baum mit kleinerer Wurzel (grau) den anderen Baum (schwarz) als linken Teilbaum hinzu. Am Ende erhält man so den unteren Baum mit Grad 3.

Die zentrale Operation ist das Verschmelzen zweier Heaps (merge), da diese als Unterprogramm aller anderen Operationen verwendet wird. Die Operation erfolgt ähnlich der bitweisen Addition von Dualzahlen. In diesem Fall entspricht dies der Addition der Anzahl der Elemente n₁ und n₂ der zu verschmelzenden Heaps.

Dazu werden simultan die Listen der beiden Heaps beginnend bei den Bäumen niedrigster Ordnung durchlaufen. In einer speziellen Variablen wird – ähnlich der bitweisen Addition – ggf. ein Übertrag (in Form eines Baumes) festgehalten. Anfangs ist dieser Übertrag leer.

Sei nun x die höchste Binärstelle von $n_{1}+n_{2}$ verschieden von 0, das heißt $x=\log _{2}(n_{1}+n_{2}+1)-1$ . Zu jeder natürlichen Zahl k mit $0\leq k\leq x$ wird nun in aufsteigender Reihenfolge die Anzahl der Bäume mit Ordnung k in beiden Heaps und in der Übertragsvariablen betrachtet. Ist diese

0, so passiert nichts.
1, so wird der entsprechende Baum in den neuen Heap übernommen und der Übertrag ggf. geleert.
2, so wird der Baum, dessen Schlüssel an der Wurzel größer ist, zum am weitesten links stehenden Kind des anderen Baumes gemacht und der so entstehende Baum der Ordnung k+1 als Übertrag behalten.
3, so wird der Baum aus dem Übertrag in den neuen Heap übernommen und von den beiden Bäumen in den Heaps wird der Baum, dessen Schlüssel an der Wurzel größer ist zum am weitesten links stehenden Kind des anderen Baumes gemacht und der so entstehende Baum der Ordnung k+1 als Übertrag behalten.

Jeder dieser Schritte lässt sich in konstanter Zeit durchführen. Da maximal $\log _{2}(n_{1}+n_{2}+1)$ derartige Schritte getätigt werden, benötigt die Operation im schlimmsten Fall nur logarithmisch viel Zeit.

Entfernen eines Elementes (remove)

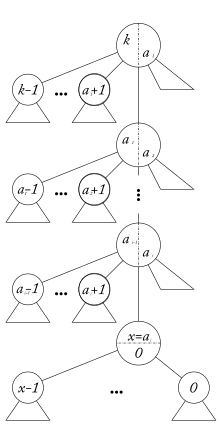
Aufspalten eines Binomial-Baumes mittels split. Dreiecke symbolisieren die neuen Teilbäume. Die Beschriftung der Knoten bezeichnet deren Ordnung vor beziehungsweise nach dem Aufspalten. Es gilt k>a₁>a₂>...>a_i=x, wobei i+1 die Tiefe von Knoten X im Baum ist.

Neben merge ist das Entfernen eines Elementes (remove) die anspruchsvollste Operation. Sei X das zu entfernende Element, seine Ordnung x und T der Binomial-Baum, der dieses Element enthält und dessen Ordnung k beträgt. Ausgehend von X muss der Binomial-Baum, der das Element enthält, geeignet in kleinere Binomial-Bäume aufgespalten werden. Dieses Aufspalten des Baumes geschieht am einfachsten mit einer rekursiven Funktion split, der als Argument ein Knoten im Baum übergeben wird. Anfangs ist X selbst das Argument. Sofern das übergebene Argument einen Elternknoten besitzt, ruft sich die Funktion zuerst selbst mit diesem als Argument auf und entfernt anschließend solange das am weitesten links stehende Kind des Vaters – also das Kind mit höchster Ordnung – bis das Argument selbst aus dem Baum entfernt wurde.

Da das Entfernen des am weitesten links stehenden Elementes gerade die umgekehrte Operation zum oben dargestellten rekursiven Aufbau der Binomial-Bäume darstellt, sind die so abgespaltenen Bäume und der Rest weiterhin Binomial-Bäume. Ferner ist X nun Wurzel eines Baumes und es lässt sich zeigen, dass der ursprüngliche Baum nun in genau 2 Binomial-Bäume der Ordnung x sowie in jeweils einen Binomial-Baum der Ordnung x+1, x+2, ..., k-1 zerfallen ist. Werden nun noch in gleicher Weise alle Kinder von X entfernt, so ist X vollständig isoliert und kann problemlos gelöscht werden. Dabei entsteht aus den Kindern für jedes j in {0, ..., x-1} jeweils genau ein Binomial-Baum der Ordnung j. Insgesamt bleibt also für jedes j aus {0, ..., k-1} ein Binomial-Baum der Ordnung j übrig. Diese Bäume bilden zusammen wieder einen Binomial-Heap, der mittels merge mit dem Rest des Heaps verschmolzen werden kann.

Das Abspalten des am weitesten links stehenden Elementes ist in konstanter Zeit möglich. Da der ursprüngliche Baum genau k mal aufgespalten wird, der Binomial-Heap aber mindestens 2^k Elemente enthält, benötigt diese Operation im Worst-Case nur logarithmisch viel Zeit. Da das anschließende merge selbst auch nur logarithmisch viel Zeit benötigt ist auch die Gesamtlaufzeit im schlimmsten Fall logarithmisch zur Anzahl der Elemente im Heap.

Weitere Operationen

Die übrigen Operationen gestalten sich nun sehr einfach.

Um ein neues Element einzufügen (insert), wird einfach ein neuer Heap erzeugt, der nur dieses eine Element enthält und dieser mittels merge mit dem eigentlichen Heap verschmolzen.
Um ein Element mit minimalem Schlüssel zu entnehmen (extractMin), braucht lediglich das Minimum der Wurzeln gefunden zu werden, indem die Liste der Wurzeln einmal durchlaufen wird und das gefundene Element mit remove entfernt und zurückgegeben wird.
Um den Schlüssel eines Elementes zu verändern (changeKey) wird dieses mit remove zunächst entfernt, dann dessen Schlüssel geändert und anschließend mit insert wieder eingefügt.

Bemerkungen

Die Operationen remove und changeKey setzen voraus, dass die Position der entsprechenden Elemente im Heap bekannt ist. Im Allgemeinen ist es nämlich nicht möglich, effizient ein Element im Heap zu suchen. Daher muss die Operation insert einen Zeiger auf den Behälter für das eingefügte Element zurückliefern, den sich das aufrufende Programm im Bedarfsfall an geeigneter Stelle merkt.

Zu der hier dargestellten Implementierung gibt es noch eine Alternative. Diese gestattet aber nur das Verringern des Schlüssels eines Elementes. Entsprechend heißt die Operation dann nicht changeKey, sondern decreaseKey. Dabei wird statt remove die Operation decreaseKey direkt implementiert. Diese tauscht den Schlüssel einfach aus und stellt die Heap-Bedingung dadurch wieder her, dass Element und Schlüssel in den tragenden Behältern solange mit denen des Vaters getauscht werden, bis die Heap-Bedingung wieder erfüllt ist. Die Operation remove wird dann so implementiert, dass mit decreaseKey der Schlüssel des Elementes quasi unendlich klein gemacht wird, so dass das Element an die Wurzel seines Binomial-Baumes wandert. Anschließend können die Kinder der neuen Wurzel entfernt und mit merge wieder in den Baum eingefügt werden.

Problematisch an diesem Verfahren ist, dass nach einem decreaseKey die Zuordnung der Elemente zu ihren Behältern nicht mehr stimmt. Die Änderungen müssen dem aufrufenden Programm also noch irgendwie mitgeteilt werden.

Literatur

Thomas H Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein: Algorithmen – eine Einführung. Oldenbourg, München, Wien 2004, ISBN 3-486-27515-1 (Originaltitel: Introduction to algorithms. Übersetzt von Karen Lippert, Micaela Krieger-Hauwede).
Jean Vuillemin: A data structure for manipulating priority queues. Communications of the ACM 21, 1978, S. 309–314.

Weblinks

@1@2Vorlage:Toter Link/www.cs.yorku.ca(Seite nicht mehr abrufbar, Suche in Webarchiven: Simulation eines Binomial-Heaps) (Java-Applet, englisch)
@1@2(Seite nicht mehr abrufbar, Suche in Webarchiven: Lernprogramm zum Binomial Heap mit Animationen und interaktiven Aufgaben) (Universität Oldenburg)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.