Heapsort

Heapsort („Haldensortierung“) ist ein in den 1960ern von Robert W. Floyd und J. W. J. Williams entwickeltes Sortierverfahren. Seine Komplexität ist bei einem Array der Länge $n$ in der Landau-Notation ausgedrückt in ${\mathcal {O}}(n\cdot \log n)$ und ist damit asymptotisch optimal für Sortieren per Vergleich. Heapsort arbeitet zwar in-place, ist jedoch nicht stabil. Der Heapsort-Algorithmus verwendet einen binären Heap als zentrale Datenstruktur. Heapsort kann als eine Verbesserung von Selectionsort verstanden werden und ist mit Treesort verwandt.

Der Heapsort-Algorithmus beim Sortieren eines Arrays aus permutierten Werten. Der Algorithmus besteht aus zwei Schritten; im vorbereitenden Schritt wird das Array zu einem binären Heap umgeordnet, dessen Baumstruktur vor dem eigentlichen Sortierschritt kurz eingeblendet wird.

Beschreibung

Die Eingabe ist ein Array mit zu sortierenden Elementen. Als erstes wird die Eingabe in einen binären Max-Heap überführt. Aus der Heap-Eigenschaft folgt direkt, dass nun an der ersten Array-Position das größte Element steht. Dieses wird mit dem letzten Array-Element vertauscht und die Heap-Array-Größe um 1 verringert, ohne den Speicher freizugeben. Die neue Wurzel des Heaps kann die Heap-Eigenschaft verletzen. Die Heapify-Operation korrigiert gegebenenfalls den Heap, so dass nun das nächstgrößere bzw. gleich große Element an der ersten Array-Position steht. Die Vertausch-, Verkleiner- und Heapify-Schritte werden so lange wiederholt, bis die Heap-Größe 1 ist. Danach enthält das Eingabe-Array die Elemente in aufsteigend sortierter Reihenfolge. In Pseudocode:

heapsort(Array A)
  build(A)
  assert(isHeap(A, 0))
  tmp = A.size
  while (A.size > 1)
    A.swap(0, A.size - 1)
    A.size = A.size - 1
    heapify(A)
    assert(isHeap(A, 0))
  A.size = tmp
  assert(isSorted(A))

Bei einer Sortierung in absteigender Reihenfolge wird statt des Max-Heaps ein Min-Heap verwendet. In einem Min-Heap steht an erster Stelle das kleinste Element. Gemäß der Definition von einem binären Heap wird die Abfolge der Elemente in einem Heap durch eine Vergleichsoperation (siehe Ordnungsrelation) bestimmt, die eine totale Ordnung auf den Elementen definiert. In einem Min-Heap ist das die $<$ -Relation und in einem Max-Heap die $>$ -Relation. Der Pseudocode abstrahiert von der Vergleichsoperation.

Die zu sortierenden Elemente werden auch als Schlüssel bezeichnet. Pro Index-Position kann das Eingabe-Array mehrere Datenkomponenten enthalten. In dem Fall muss eine Komponente als Sortierschlüssel definiert werden, auf der die Vergleichsoperation arbeitet. Die Vertauschoperation vertauscht komplette Array-Einträge.

Die assert-Operation im Pseudocode dokumentiert, welche Eigenschaften das Array nach welchen Algorithmus-Schritten korrekterweise erfüllt bzw. erfüllen muss.

Beispiel

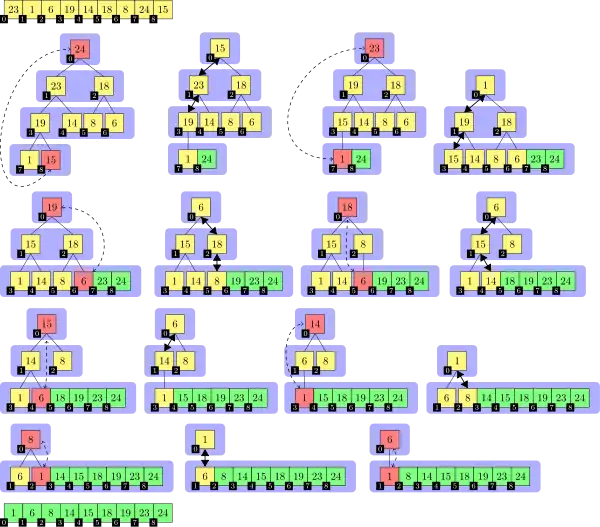
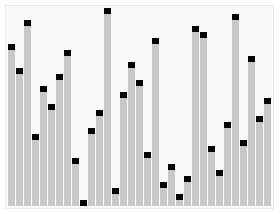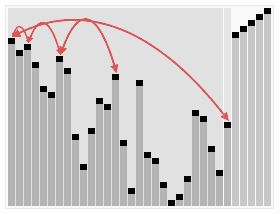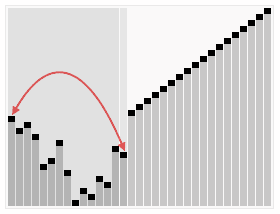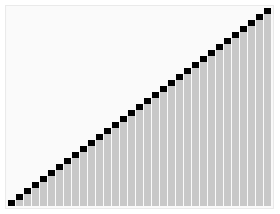
Ein Beispiel für Heapsort an einer Zahlenfolge

In der Abbildung wird die Sortierung der Beispielzahlenfolge

 23 1 6 19 14 18 8 24 15

mit dem Heapsort-Algorithmus dargestellt. Die einzelnen Teilbilder sind von links nach rechts und von oben nach unten chronologisch angeordnet. Im ersten Teilbild ist die unsortierte Eingabe und im letzten die sortierte Ausgabe abgebildet. Der Übergang vom ersten zum zweiten Teilbild entspricht der Heapifizierung des Eingabe-Arrays. Die an einer Swap-Operation beteiligten Elemente sind rot und mit unterbrochenen Pfeilen markiert, dicke Doppelpfeile bezeichnen die an einer Heapify-Operation beteiligten Elemente und grün markierte Elemente zeigen den schon sortierten Anteil des Arrays an. Die Element-Indizes sind mit kleinen schwarzen Knoten eingezeichnet, jeweils links unten von dem Element-Wert. Eine blaue Hinterlegung der Array-Elemente indiziert die Laufzeit der Heapsort-Prozedur.

Die Indizes entsprechen einer aufsteigenden Nummerierung nach Level-Order, beginnend mit 0. In einer Implementierung des Algorithmus ist die Baumstruktur implizit und das Array der Elemente zusammenhängend, was durch die Platzierung der Element-Indizes in der Abbildung angedeutet wird.

Effizienz

Man kann zeigen, dass der Aufbau des Heaps, in Landau-Notation ausgedrückt, in ${\mathcal {O}}(n)$ Schritten ablaufen kann. In einem großen, zufällig verteilten Datenfeld (100 bis 10¹⁰ Datenelemente) sind durchschnittlich mehr als 4, aber weniger als 5 signifikante Sortieroperationen pro Element nötig (2,5 Datenvergleiche und 2,5 Zuweisungen). Dies liegt daran, dass ein zufälliges Element mit exponentiell zunehmender Wahrscheinlichkeit einen geeigneten Vaterknoten findet (60 %, 85 %, 93 %, 97 %, …).

Die Heapify-Operation benötigt im ungünstigsten Fall $\Theta (\log n)$ Schritte. Dies ist bei exakt inverser Reihenfolge der Fall. In dem durchschnittlichen Fall werden etwa die Hälfte der Operationen des ungünstigsten Falls und somit ebenfalls $\Theta (\log n)$ Schritte benötigt. Günstig ist nur ein Feld, dessen Elemente fast alle den gleichen Wert haben. Sind aber nur weniger als ca. 80 % der Daten identisch, dann entspricht die Laufzeit bereits dem durchschnittlichen Fall. Eine vorteilhafte Anordnung von Daten mit mehreren verschiedenen Werten ist prinzipbedingt unmöglich, da dies der Heapcharakteristik widerspricht.

Den Worst Case stellen mit $\Theta (n\cdot \log n)$ weitgehend vorsortierte Daten dar, weil der Heapaufbau de facto eine schrittweise vollständige Invertierung der Sortierreihenfolge darstellt. Der günstigste, aber unwahrscheinliche Fall ist ein bereits umgekehrt sortiertes Datenfeld (1 Vergleich pro Element, keine Zuweisung). Gleiches gilt, wenn fast alle Daten identisch sind.

Auf heterogenen Daten – vorsortiert oder nicht – dominiert Heapify mit wenigstens über 60 % der Zeit, meistens über 80 %. Somit garantiert Heapsort eine Gesamtlaufzeit von ${\mathcal {O}}(n\cdot \log n)$ . Auch im besten Fall wird eine Laufzeit von $\Theta (n\cdot \log n)$ benötigt.[1][2]

Eine Variante von Heapsort benötigt im Worst Case $n\cdot \log _{2}(n)+n\cdot \log _{2}(\log _{2}(n))+n$ Vergleiche.[3]

Abgrenzung

Im Durchschnitt ist Heapsort nur dann schneller als Quicksort, wenn Vergleiche auf den zu sortierenden Daten sehr aufwendig sind und gleichzeitig eine für Quicksort ungünstige Datenanordnung besteht, z. B. viele gleiche Elemente. In der Praxis ist bei unsortierten oder teilweise vorsortierten Daten Quicksort oder Introsort um einen konstanten Faktor von 2 bis 5 schneller als Heapsort. Dies wird jedoch kontrovers diskutiert und es gibt Analysen, die Heapsort vorne sehen, sowohl aus Implementierungs- wie auch aus informationstheoretischen Überlegungen.[4][5] Allerdings spricht das Worst-Case-Verhalten von ${\mathcal {O}}(n\cdot \log n)$ gegenüber $\Theta (n^{2})$ bei Quicksort für Heapsort. Introsort ist dagegen in fast allen Fällen schneller als Heapsort, lediglich in entarteten Fällen 20 % bis 30 % langsamer.

Bottom-Up-Heapsort

Die wichtigste Variante des Heapsort-Algorithmus ist Bottom-Up-Heapsort, das häufig fast die Hälfte der nötigen Vergleichsoperationen einsparen kann und sich folglich besonders da rentiert, wo Vergleiche aufwendig sind.

Bottom-Up-Heapsort ist ein Sortieralgorithmus, der u. a. 1990 von Ingo Wegener vorgestellt wurde und im Durchschnitt besser als Quicksort arbeitet, falls man Vergleichsoperationen hinreichend stark gewichtet. Es ist eine Variante von Heapsort, die vor allem zur Sortierung sehr großer Datenmengen geeignet ist, wenn (im Vergleich zu den notwendigen Vertauschungsoperationen) ein relativ hoher Aufwand pro Vergleichsoperation erforderlich ist.

Diese Variante wurde allerdings bereits 1986 von Svante Carlsson analysiert, der letztlich eine weitere Variante fand, die sogar eine Worst-Case-Laufzeit von nur $n\cdot \log _{2}(n)+{\mathcal {O}}(n\cdot \log _{2}(\log _{2}(n)))$ Vergleichen hat. Entdeckt wurde dieser Bottom-Up-Heapsort bereits von Robert W Floyd, der aber das Laufzeitverhalten dieser Variante nicht beweisen konnte.

Bottom-Up-Heapsort benötigt zum Sortieren einer Folge von $n$ Elementen im Worst Case ${\tfrac {3}{2}}\cdot n\cdot \log _{2}(n)+2\cdot n$ Vergleiche. Im Durchschnitt sind es $n\cdot \log _{2}(n)+{\mathcal {O}}(n)$ Vergleiche.

Prinzip der Sortierung

Beim Sortieren mit normalem Heapsort finden beim Absenken eines Elements zwei Vergleiche pro Ebene statt:

Welcher der beiden Nachfolgeknoten des abzusenkenden Elements ist größer?
Ist der nun bestimmte Nachfolgeknoten größer als das abzusenkende Element?

Nachdem ein Binärbaum zur Hälfte aus Blättern besteht und zudem beim Sortieren ehemalige Blätter mit ohnehin schon eher niedrigen Werten abgesenkt werden, ist es wahrscheinlich, dass ein Element bis zur Blattebene oder in deren Nähe abgesenkt werden muss. Deshalb kann es lohnend sein, auf den zweiten Vergleich zu verzichten und auf Verdacht bis zur Blattebene abzusenken.

In einem zweiten Schritt wird dann rückwärts überprüft, wie weit das Element wieder angehoben werden muss. Im günstigsten Fall (sehr große Felder mit nur wenigen Dubletten) kann dabei fast die Hälfte der insgesamt nötigen Vergleiche bei mäßigem Zusatzaufwand eingespart werden.

Weniger geeignet ist Bottom-Up-Heapsort zur Sortierung kleinerer Felder mit einfacher numerischer Vergleichsoperation und dann, wenn im Feld sehr viele Elemente gleichwertig sind. Dann stimmt die Annahme nicht, dass meist bis in die Nähe der Blattebene abgesenkt werden muss.

Algorithmus

Konkret wird der Heapsort-Algorithmus, was das Absenken betrifft, wie folgt verändert:

Zunächst wird der Pfad, in welchem das Wurzelelement versenkt werden soll, bestimmt. Dies geschieht durch die Ermittlung des jeweils größten Kindes (Pfad maximaler Kinder). Danach wird dieser bestimmte Pfad von unten nach oben vom Blatt in Richtung Wurzel durchlaufen. Hierbei wird bei jedem besuchten Knoten verglichen, ob er größer als das abzusenkende Wurzelelement ist. Ist dem so, wird das Wurzelelement an die Position des zuletzt besuchten Knotens kopiert und vorher der restliche Pfad um eine Ebene nach oben verschoben.

Alternativ kann man auch die Verschiebung von vornherein auf Verdacht bis zur Blattebene durchführen und später – soweit notwendig – wieder rückgängig machen. Wo Kopien relativ günstig durchgeführt werden können (weil etwa nur ein Zeiger kopiert wird), kann das insgesamt vorteilhaft sein.

Beispiel

Heap: [9, 23, 24, 20, 18, 14, 17, 13, 15, 11, 10, 5, 7, 3, 2]

Baumstruktur:

            9
       /         \
      23         24
    /   \       /  \
   20   18     14  17
  / \   / \   / \  / \
 13 15 11 10  5  7 3  2

Das Element 9 muss abgesenkt werden, da es kleiner als mindestens ein Nachfolgeknoten ist. Es wird als erstes der Pfad der maximalen Kinder (ausgehend von der Wurzel) bestimmt. Es ergibt sich also 9 - 24 - 17 - 3. Der Algorithmus durchläuft diesen Pfad nun von unten nach oben, also 3 -> 17 -> 24 -> 9. Nun wird der Pfad vom Blattknoten (3) beginnend solange durchlaufen, bis sich ein Knoten findet, der größer als 9 ist. Der Durchlauf endet folglich bei 17. Nun werden alle Knoten ab 17 bis zum Nachfolgeknoten der Wurzel (= 17 -> 24) um eine Ebene nach oben und der Knoten 9 an die Position von 17 verschoben. Folglich ändern 17 und 24 als Nachfolgeknoten und 9 als Wurzelknoten ihren Platz.

Heap: [24, 23, 17, 20, 18, 14, 9, 13, 15, 11, 10, 5, 7, 3, 2]

Baumstruktur:

           24           -------|                      24
       /         \             |                 /         \
      23         17            9                23         17
    /   \       /  \           |               /   \      /   \
   20   18     14      <-------|              20   18    14    9
  / \   / \   / \  / \                       / \   / \   / \  / \
 13 15 11 10  5  7 3  2                     13 15 11 10 5  7  3  2

Implementierung

Einfache Beispielsimplementierung in der Programmiersprache C:

 int heapsort_bu( int * data, int n ) // zu sortierendes Feld und seine Länge
 {
   int val, parent, child;
   int root= n >> 1;                  // erstes Blatt im Baum
   int count= 0;                      // Zähler für Anzahl der Vergleiche

   for ( ; ; )
   {
     if ( root ) {                    // Teil 1: Konstruktion des Heaps
       parent= --root;
       val= data[root];               // zu versickernder Wert
     }
     else
     if ( --n ) {                     // Teil 2: eigentliche Sortierung
       val= data[n];                  // zu versickernder Wert vom Heap-Ende
       data[n]= data[0];              // Spitze des Heaps hinter den Heap in
       parent= 0;                     //   den sortierten Bereich verschieben
     }
     else                             // Heap ist leer; Sortierung beendet
       break;

     while ( (child= (parent + 1) << 1) < n )  // zweites (!) Kind;
     {                                         // Abbruch am Ende des Heaps
       if ( ++count, data[child-1] > data[child] )  // größeres Kind wählen
         --child;

       data[parent]= data[child];     // größeres Kind nach oben rücken
       parent= child;                 // in der Ebene darunter weitersuchen
     }

     if ( child == n )                // ein einzelnes Kind am Heap-Ende
     {                                //   ist übersprungen worden
       if ( ++count, data[--child] >= val ) {  // größer als der zu versick-
         data[parent]= data[child];   //   ernde Wert, also noch nach oben
         data[child]= val;            // versickerten Wert eintragen
         continue;
       }

       child= parent;                 // 1 Ebene nach oben zurück
     }
     else
     {
       if ( ++count, data[parent] >= val ) {  // das Blatt ist größer als der
         data[parent]= val;           //   zu versickernde Wert, der damit
         continue;                    //   direkt eingetragen werden kann
       }

       child= (parent - 1) >> 1;      // 2 Ebenen nach oben zurück
     }

     while ( child != root )          // maximal zum Ausgangspunkt zurück
     {
       parent= (child - 1) >> 1;      // den Vergleichswert haben wir bereits
                                      //   nach oben verschoben
       if ( ++count, data[parent] >= val )  // größer als der zu versickernde
         break;                             //   Wert, also Position gefunden

       data[child]= data[parent];     // Rückverschiebung nötig
       child= parent;                 // 1 Ebene nach oben zurück
     }

     data[child]= val;                // versickerten Wert eintragen
   }

   return count;
 }

Zu Vergleichszwecken gibt die Funktion die Anzahl der durchgeführten Vergleiche zurück.

Andere Varianten

Smoothsort

Normales Heapsort sortiert bereits weitgehend vorsortierte Felder nicht schneller als andere. Die größten Elemente müssen immer erst ganz nach vorn an die Spitze des Heaps wandern, bevor sie wieder nach hinten kopiert werden. Smoothsort ändert das, indem es im Prinzip die Reihenfolge des Heaps umdreht. Dabei ist allerdings beträchtlicher Aufwand nötig, um den Heapstatus beim Sortieren aufrechtzuerhalten. Smoothsort benötigt eine lineare Laufzeit von ${\mathcal {O}}(n)$ , um ein vorsortiertes Array (Best Case) zu verarbeiten, und genauso wie andere Varianten eine Laufzeit von ${\mathcal {O}}(n\cdot \log n)$ im Durchschnitt und im Worst Case, und erzielt bei vielen nahezu sortierten Eingaben eine nahezu lineare Leistung. Es werden jedoch nicht alle nahezu sortierten Sequenzen optimal verarbeitet.[6]

Ternäre Heaps

Eine andere Optimierung verwendet statt binären ternäre Heaps. Diese Heaps beruhen statt auf Binärbäumen auf Bäumen, bei denen jeder vollständig besetzte Knoten 3 Kinder hat. Damit kann die Zahl der Vergleichsoperationen bei einigen Tausend bis einigen Millionen Elementen um etwa 3 % reduziert werden. Außerdem sinkt der sonstige Aufwand deutlich. Insbesondere müssen durch den flacheren Heap knapp ein Drittel weniger Elemente beim Versickern (Heapify) verschoben werden.

In einem binären Heap kann ein Element mit $2\cdot n$ Vergleichen um $n$ Ebenen abgesenkt werden und hat dabei durchschnittlich ${\tfrac {3}{2}}\cdot (2^{n}-1)$ Indizes übersprungen. In einem ternären Heap kann ein Element mit $3\cdot m$ Vergleichen um $m$ Ebenen abgesenkt werden und hat dabei durchschnittlich $3^{m}-1$ Indizes übersprungen. Wenn bei gleicher Reichweite der relative Aufwand $x:={\tfrac {3\cdot m}{2\cdot n}}$ ist, dann gilt

{\frac {3}{2}}\cdot (2^{n}-1)=3^{\frac {2\cdot n\cdot x}{3}}-1

, also

x={\frac {3}{2\cdot n}}\cdot \log _{3}\left({\frac {3}{2}}\cdot 2^{n}-{\frac {1}{2}}\right)=_{n\to \infty }{\frac {3}{2}}\cdot \log _{3}(2)\approx 0{,}946

Bei $n=18$ (realistisch bei knapp 1 Million Elementen) ergibt sich 0,977. Die 1 wird oberhalb von $n=10$ unterschritten. In der Praxis ist die Ersparnis etwas größer, u. a. deswegen, weil ternäre Bäume mehr Blätter haben und deshalb beim Aufbau des Heaps weniger Elemente versickert werden müssen.

Insgesamt kann die Sortierung mit ternären Heaps bei großen Feldern (mehrere Millionen Elemente) und einfacher Vergleichsoperation 20 % bis 30 % Zeit einsparen. Bei kleinen Feldern (bis etwa tausend Elemente) lohnen sich ternäre Heaps nicht oder sind sogar langsamer.

n-äre Heaps

Bei noch breiteren Bäumen bzw. flacheren Heaps steigt die Zahl der nötigen Vergleichsoperationen wieder an. Trotzdem können sie vorteilhaft sein, weil der sonstige Aufwand vor allem der für das Kopieren von Elementen weiter sinkt und geordneter auf die Elemente zugegriffen wird, was die Effizienz von Caches erhöhen kann. Sofern bei großen Feldern nur ein einfacher numerischer Vergleich durchzuführen ist und Schreiboperationen relativ langsam sind, können 8 oder mehr Kinder pro Knoten optimal sein.

Einfache Beispielsimplementierung mit Heaps beliebiger Arität (WIDTH, mit WIDTH>=2) in der Programmiersprache C:

static size_t heapify(int *data, size_t n, size_t WIDTH, size_t root)
{
  assert(root < n);
  size_t count = 0;
  int val = data[root];
  size_t parent = root;
  size_t child = 0;
  assert(parent * WIDTH >= parent); // Overflow-Test
  while ( (child = parent * WIDTH + 1) < n )  // erstes Kind;
  {                                           // Abbruch am Ende des Heaps
    size_t w = n - child < WIDTH ?
      n - child : WIDTH;            // Anzahl der vorhandenen Geschwister

    count += w;

    size_t max = 0;
    for (size_t i = 1; i < w; ++i )  // größtes Kind suchen
      if (data[child+i] > data[child+max])
        max = i;
    child += max;

    if (data[child] <= val)        // kein Kind mehr größer als der
      break;                        //   zu versickernde Wert

    data[parent] = data[child];     // größtes Kind nach oben rücken
    parent = child;                 // in der Ebene darunter weitermachen
  }
  data[parent] = val;               // gesiebten Wert eintragen
  return count;
}

size_t nhsort(int * data, size_t n, size_t WIDTH)
{
  assert(WIDTH > 1);
  if (n < 2)
    return 0;
  size_t m = (n + WIDTH - 2) / WIDTH;  // erstes Blatt im Baum
  int count = 0;                       // Zähler für Anzahl der Vergleiche

  assert(m > 0);
  for (size_t r = m; r > 0; --r)       // Teil 1: Konstruktion des Heaps
    count += heapify(data, n, WIDTH, r-1);
  for (size_t i = n - 1; i > 0; --i) { // Teil 2: eigentliche Sortierung
    int tmp = data[0];                 // Spitze des Heaps hinter den Heap in
    data[0] = data[i];
    data[i] = tmp;                     //   den sortierten Bereich verschieben
    count += heapify(data, i, WIDTH, 0);
  }
  return count;
}

Zu Vergleichszwecken gibt die Funktion die Anzahl der durchgeführten Vergleiche zurück.

Siehe auch

Hybridsort

Literatur

Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein: Introduction to Algorithms. 2. Auflage. MIT Press, Cambridge MA 2001, ISBN 0-262-03293-7, S. 135.
Donald E. Knuth: The Art of Computer Programming: Volume 3 Sorting and Searching. 2. Auflage. Addison-Wesley, Reading MA 1997, ISBN 0-201-89685-0, S. 145.
Robert W. Floyd: Algorithm 245: Treesort 3. In: Communications of the ACM. Band 7, Nr. 12, Dezember 1964, S. 701.
J. W. J. Williams: Algorithm 232: Heapsort. In: Communications of the ACM. Band 7, Nr. 6, Juni 1964, S. 347–348.
Robert W. Floyd: Algorithm 113: Treesort. In: Communications of the ACM. Band 5, Nr. 8, August 1962, S. 434.

Weblinks

Wikibooks: Heapsort – Implementierungen in der Algorithmensammlung

Commons: Heap sort – Sammlung von Bildern, Videos und Audiodateien

Video zur Visualisierung von Heap Sort
Analyse von Heapsort und Java-Applet zur Demonstration (FH Flensburg)
VisuSort Framework – Visualisierung diverser Sortieralgorithmen (Windows)
sortieralgorithmen.de
Heapsort in Python3.2 – Heap queue algorithm

Einzelnachweise

Russel Schaffer, Robert Sedgewick: The analysis of heapsort. In: Journal of Algorithms, Volume 15, Issue 1. Juli 1993. S. 76–100, ISSN 0196-6774
Bela Bollobas, Trevor I. Fenner, Alan M. Frieze: On the best case of heapsort. In: Journal of Algorithms, Volume 20, Issue 2. März 1996. S. 205–217. ISSN 0196-6774
Gu Xunrang, Zhu Yuzhang: Optimal heapsort algorithm
Paul Hsieh: Sorting revisited.. azillionmonkeys.com. 2004. Abgerufen am 26. April 2010.
David MacKay: Heapsort, Quicksort, and Entropy. aims.ac.za/~mackay. 1. Dezember 2005. Archiviert vom Original am 7. Juni 2007. Abgerufen am 26. April 2010.
Stefan Hertel: Smoothsort’s behavior on presorted sequences. (PDF) In: Information Processing Letters. 16, Nr. 4, 13. Mai 1983, S. 165–170. doi:10.1016/0020-0190(83)90116-3.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Russel Schaffer, Robert Sedgewick: The analysis of heapsort. In: Journal of Algorithms, Volume 15, Issue 1. Juli 1993. S. 76–100, ISSN 0196-6774

[2] Bela Bollobas, Trevor I. Fenner, Alan M. Frieze: On the best case of heapsort. In: Journal of Algorithms, Volume 20, Issue 2. März 1996. S. 205–217. ISSN 0196-6774

[3] Gu Xunrang, Zhu Yuzhang: Optimal heapsort algorithm

[4] Paul Hsieh: Sorting revisited.. azillionmonkeys.com. 2004. Abgerufen am 26. April 2010.

[5] David MacKay: Heapsort, Quicksort, and Entropy. aims.ac.za/~mackay. 1. Dezember 2005. Archiviert vom Original am 7. Juni 2007. Abgerufen am 26. April 2010.

[6] Stefan Hertel: Smoothsort’s behavior on presorted sequences. (PDF) In: Information Processing Letters. 16, Nr. 4, 13. Mai 1983, S. 165–170. doi:10.1016/0020-0190(83)90116-3.