Fermi-Fläche
Die Fermi-Fläche (benannt nach dem italienischen Physiker Enrico Fermi) ist eine mathematische Konstruktion, die in der Festkörperphysik zur Beschreibung der Energiezustände der Elektronen eines Metalls benutzt wird.
Bedeutung
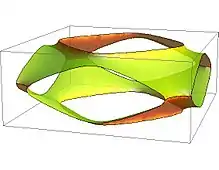
Die Fermi-Fläche ist eine Fläche konstanter Energie, und zwar nicht im gewöhnlichen Ortsraum, sondern im reziproken Raum. Dies ist der Impulsraum, den man rein mathematisch durch eine Fourier-Transformation aus dem Ortsraum erhält. Die Benutzung dieses abstrakten Raumbegriffs hat bei der Beschreibung kristalliner Systeme viele Vorteile, z. B. lassen sich die Reflexe bei der Röntgenstrukturanalyse direkt dem reziproken Gitter zuordnen.
Insbesondere lässt sich im reziproken Raum die Energie direkt als Funktion des Impulses der Elektronen darstellen. Bei Metallen sind die Energieniveaus des Leitungsbandes im energieärmsten Zustand (am absoluten Nullpunkt) nur bis zu einer bestimmten Energie, der Fermi-Energie, besetzt. Die Menge der Punkte, auf die Impulsvektoren von Elektronen mit der Fermi-Energie zeigen, bilden eine geschlossene Fläche bzw. wenige geschlossene Flächen, die Fermi-Fläche(n) genannt wird bzw. werden. Mit ihrer Hilfe lassen sich viele elektronische und magnetische Eigenschaften des Metalls beschreiben. Beispielsweise tragen nur die Elektronen mit Fermi-Energie und somit an der Fermi-Fläche zum elektrischen Strom bei.
Die Fermi-Flächen der Alkalimetalle sowie der Metalle Cu, Ag und Au sind relativ einfach, weil alle Leitungselektronen innerhalb der ersten Brillouin-Zone liegen. Die Fermi-Flächen sind daher nahezu Kugeln. Bei Cu, Ag und Au haben die Fermiflächen allerdings in den 111-Richtungen jeweils einen „Hals“ zum Rand der Brillouin-Zone; auch bei Cs treten kleine „Hälse“ auf. Die Flächen und Hälse lassen sich z. B. unter Ausnutzung des De-Haas-van-Alphen-Effekts experimentell vermessen.
Ferromagnetische Metalle haben im einfachsten Fall zwei Fermi-Flächen wegen der zwei möglichen Orientierungen des Elektronenspins.
Isolatoren und undotierte Halbleiter haben keine Fermi-Fläche, weil bei ihnen die Fermi-Energie in die Bandlücke fällt und es somit keine Elektronenzustände gibt, deren Energie gleich der Fermi-Energie ist. Durch Einbringen zusätzlicher Ladungsträger in einen Halbleiter (Donator- oder Akzeptordotierung) kann allerdings das Fermi-Niveau verschoben und damit die Ausbildung einer Fermi-Fläche erzwungen werden.
Hieraus folgt auch die vermutlich genaueste Definition des Begriffs „Metall“ im Sinne einer Abgrenzung zu anderen (festen) Stoffen: Ein Metall ist ein Festkörper mit einer Fermi-Fläche. Nach dieser Definition wäre flüssiges Quecksilber (und Schmelzen anderer „Metalle“) kein Metall.
Fermi-Kugel
In einem freien Elektronengas werden die Zustände im reziproken Raum energetisch sukzessive aufgefüllt, d. h. beginnend mit einem Wellenvektor bis zu einem Grenzwellenvektor werden die Zustände mit jeweils zwei Spin-Einstellungen besetzt, wobei als Fermi-Wellenvektor bezeichnet wird. Die Zustände liegen daher im reziproken Raum alle innerhalb einer Kugel, der Fermi-Kugel. Die Elektronen auf der Oberfläche der Fermi-Kugel haben die Energie
- ,
wobei auch als Fermi-Impuls bezeichnet wird.
Das Volumen der Fermi-Kugel im reziproken (dreidimensionalen) Raum beträgt dann
- .
Das Modell des freien Elektronengases trifft näherungsweise für Metalle zu, insbesondere für Alkali-Metalle wie Natrium oder Kalium, weil diese nur ein Elektron pro Elementarzelle als freien Ladungsträger haben. Durch die kugelförmige Gestalt lassen sich manche physikalischen Berechnungen vereinfachen, um zu einem qualitativen Verständnis zu gelangen.
Weblinks
- Grafische Darstellung der Fermi-Flächen
- Zusammenfassung Fermi-Flächen (Memento vom 29. September 2007 im Internet Archive) (PDF; 295 kB)
Literatur
- Charles Kittel: Introduction to Solid State Physics. 1. Ausgabe 1953 bis 14. Ausgabe 2005, ISBN 0-471-41526-X (dt. Einführung in die Festkörperphysik. Oldenbourg, ISBN 3-486-57723-9)