Fehlstand
Unter Fehlstand, Fehlstellung oder Inversion einer Permutation versteht man in der Kombinatorik ein Paar von Elementen einer geordneten Menge, deren Reihenfolge durch die Permutation vertauscht wird. Die Anzahl der Fehlstände einer Permutation heißt Fehlstandszahl oder Inversionszahl der Permutation. Über die Fehlstandszahl lässt sich das Vorzeichen einer Permutation ermitteln, wobei eine gerade Permutation eine gerade Fehlstandszahl und eine ungerade Permutation eine ungerade Fehlstandszahl aufweist.

Es gibt verschiedene Möglichkeiten zur Darstellung der Fehlstände einer Permutation, beispielsweise über die Inversionstafel, den Lehmer-Code oder das Rothe-Diagramm. Fasst man die Einträge der Inversionstafel oder des Lehmer-Codes als Zahl in einem fakultätsbasierten Zahlensystem auf, kann jeder Permutation eine eindeutige Nummer zugewiesen werden. Weiter lässt sich mit Hilfe der Fehlstände auf der Menge der Permutationen eine partielle Ordnung definieren.
Nachdem die Fehlstandszahl einer Permutation als Maß für die Unordnung der durch die Permutation vertauschten Zahlen angesehen werden kann, spielen Fehlstände eine wichtige Rolle bei der Analyse von Sortierverfahren.
Definition
Ist die symmetrische Gruppe aller Permutationen der Menge , dann ist ein Fehlstand einer Permutation ein Paar , für das
- und
gilt. Die Menge der Fehlstände einer Permutation ist dann durch
- .
gegeben. Gelegentlich wird in der Literatur anstelle des Paares auch das Paar als Fehlstand bezeichnet.
Allgemeiner können auch Permutationen beliebiger endlicher geordneter Mengen betrachtet werden, für die mathematische Analyse kann man sich jedoch auf die ersten natürlichen Zahlen beschränken.
Beispiele
Konkretes Beispiel
Die Menge der Fehlstände der Permutation
ist
- .
Man kann diese fünf Fehlstände dadurch ermitteln, dass man in der zweiten Zeile für jede Zahl von bis alle Zahlen sucht, die größer sind und links von der Zahl stehen. Im Beispiel sind dies die Paare und . Die Fehlstände sind dann die jeweils zugehörigen Zahlenpaare der ersten Zeile. Beispielsweise ist der zu dem Paar zugehörige Fehlstand das Paar , da über der die Zahl und über der die Zahl steht.
Allgemeinere Beispiele
Die identische Permutation ist die einzige Permutation ohne Fehlstände, also
- .
Eine Nachbarvertauschung generiert genau einen Fehlstand
- .
Eine Transposition mit weist die folgenden Fehlstände auf:
- .
Anzahl
Fehlstandszahl
| Nr. | Permutation | Fehlstände | Anzahl |
|---|---|---|---|
| 0 | (1,2,3) | - | 0 |
| 1 | (1,3,2) | (2,3) | 1 |
| 2 | (2,1,3) | (1,2) | 1 |
| 3 | (2,3,1) | (1,3),(2,3) | 2 |
| 4 | (3,1,2) | (1,2),(1,3) | 2 |
| 5 | (3,2,1) | (1,2),(1,3),(2,3) | 3 |
Die Anzahl der Fehlstände einer Permutation heißt Fehlstandszahl oder Inversionszahl der Permutation. Die Fehlstandszahl kann als Maß für die Unordnung der durch die Permutation vertauschten Zahlen angesehen werden. Über die Fehlstandszahl lässt sich das Vorzeichen einer Permutation ermitteln, denn es gilt
- .
Ist die Fehlstandszahl gerade, so spricht man von einer geraden Permutation, ansonsten von einer ungeraden Permutation. Die Fehlstandszahl der inversen Permutation ist identisch mit der Fehlstandszahl der Ausgangspermutation , das heißt
- ,
denn die Menge der Fehlstände der inversen Permutation hat die Darstellung[1]
- .
Verteilung
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 |
| 2 | 0 | 0 | 2 | 5 | 9 | 14 |
| 3 | 0 | 0 | 1 | 6 | 15 | 29 |
| 4 | 0 | 0 | 0 | 5 | 20 | 49 |
| 5 | 0 | 0 | 0 | 3 | 22 | 71 |
| 6 | 0 | 0 | 0 | 1 | 20 | 90 |
| 7 | 0 | 0 | 0 | 0 | 15 | 101 |
| 8 | 0 | 0 | 0 | 0 | 9 | 101 |
| 9 | 0 | 0 | 0 | 0 | 4 | 90 |
| 10 | 0 | 0 | 0 | 0 | 1 | 71 |
| 11 | 0 | 0 | 0 | 0 | 0 | 49 |
| 12 | 0 | 0 | 0 | 0 | 0 | 29 |
| 13 | 0 | 0 | 0 | 0 | 0 | 14 |
| 14 | 0 | 0 | 0 | 0 | 0 | 5 |
| 15 | 0 | 0 | 0 | 0 | 0 | 1 |
| Summe | 1 | 2 | 6 | 24 | 120 | 720 |
Die Anzahl der -stelligen Permutationen mit genau Fehlständen ist definiert als
- .
Nachdem die identische Permutation die einzige Permutation ohne Fehlstände ist, gilt für alle . Da es Nachbarvertauschungen mit genau einem Fehlstand gibt, ist weiter für alle . Die maximale Fehlstandszahl einer -stelligen Permutation beträgt
und wird genau für diejenige Permutation angenommen, die die Reihenfolge aller Zahlen umkehrt. Weiterhin gilt die Symmetrie
- .
Mit der Konvention für und erfüllen die Zahlen die Rekursion (Folge A008302 in OEIS)
und die Summendarstellung
- .
Erzeugende Funktion
Die erzeugende Funktion für die Anzahl der Fehlstände hat die verhältnismäßig einfache Form
- .
Dieses Resultat geht auf Olinde Rodrigues (1839) zurück.[2]
Erwartungswert und Varianz
Der Erwartungswert der Fehlstandszahl einer (gleichverteilt) zufälligen Permutation aus beträgt
- ,
weshalb Sortierverfahren wie Bubblesort, die pro Schritt genau einen Fehlstand beheben, nicht nur im schlechtesten Fall, sondern auch im durchschnittlichen Fall eine quadratische Laufzeit aufweisen. Für die Varianz der Fehlstandszahl einer zufälligen Permutation gilt entsprechend
- ,
wodurch auch die Standardabweichung der Fehlstandszahl mit einem Wert von etwa vergleichsweise groß ausfällt.[3] Die Anzahl der Fehlstände einer zufälligen Permutation ist für asymptotisch normalverteilt.[4]
Darstellungen
Inversionstafel
| Nr. | Permutation | Inversionstafel |
|---|---|---|
| 0 | (1,2,3) | (0,0,0) |
| 1 | (1,3,2) | (0,1,0) |
| 2 | (2,1,3) | (1,0,0) |
| 3 | (3,1,2) | (1,1,0) |
| 4 | (2,3,1) | (2,0,0) |
| 5 | (3,2,1) | (2,1,0) |
Die Inversionstafel oder der Inversionsvektor einer Permutation ordnet jeder Zahl die Anzahl der Fehlstände zu, die sie erzeugt. Bezeichnet
die Anzahl der Zahlen, die in der Tupeldarstellung von links von stehen und größer als sind, dann ist die Inversionstafel einer Permutation der Vektor
- .
Da die Zahl höchstens Fehlstände erzeugen kann, gilt und somit immer . Die Fehlstandszahl der Permutation ergibt sich dann als Summe
- .
Aus der Inversionstafel lässt sich umgekehrt die zugrundeliegende Permutation ermitteln. Hierzu bestimmt man der Reihe nach die relativen Platzierungen der Zahlen , wobei jeweils angibt, an welcher Position die Zahl innerhalb der bereits betrachteten Zahlen auftritt. Dabei steht für die erste Stelle, für die zweite Stelle und so fort. Diese Eins-zu-Eins-Korrespondenz von Permutation und zugehöriger Inversionstafel ist von großer praktischer Bedeutung, da sich kombinatorische Probleme im Zusammenhang mit Permutationen durch die Betrachtung von Inversionstafeln oft leichter lösen lassen. Der Grund hierfür liegt darin, dass die Einträge der Inversionstafel innerhalb der vorgegebenen Grenzen unabhängig voneinander gewählt werden können, während die Zahlen paarweise verschieden sein müssen.[5]
Beispiel
In obigem Beispiel ist die Inversionstafel
- .
Aus der Inversionstafel erhält man die zugrundeliegende Permutation zurück, indem man folgende Anordnungen der Reihe nach ermittelt:
- und .
Lehmer-Code
| Nr. | Permutation | Lehmer-Code |
|---|---|---|
| 0 | (1,2,3) | (0,0,0) |
| 1 | (1,3,2) | (0,1,0) |
| 2 | (2,1,3) | (1,0,0) |
| 3 | (2,3,1) | (1,1,0) |
| 4 | (3,1,2) | (2,0,0) |
| 5 | (3,2,1) | (2,1,0) |
Auf gewisse Weise dual zur Inversionstafel ist der Lehmer-Code (benannt nach Derrick Henry Lehmer), der ebenfalls die Fehlstände einer Permutation zusammenfasst. Bezeichnet
die Anzahl der Zahlen, die in der Tupeldarstellung von rechts von stehen und kleiner als sind, dann ist der Lehmer-Code einer Permutation der Vektor
- .
Auch hier gilt und somit immer . Die Fehlstandszahl der Permutation ergibt sich entsprechend als Summe
- .
Aus dem Lehmer-Code lässt sich ebenfalls die zugrundeliegende Permutation ermitteln. Hierzu notiert man zunächst alle Zahlen von bis hintereinander. Im Folgenden entfernt man aus dieser Liste jeweils im -ten Schritt die -te Zahl und notiert diese dann als . Auch hier liegt eine Eins-zu-Eins-Korrespondenz zwischen der Permutation und dem zugehörigen Lehmer-Code vor.
Beispiel
In obigem Beispiel ist der Lehmer-Code
- .
Aus dem Lehmer-Code erhält man die zugrundeliegende Permutation zurück, indem man folgende Anordnungen der Reihe nach ermittelt:
- und .
Rothe-Diagramm
| 1 | 2 | 3 | 4 | 5 | l | |
| 1 | 2 | |||||
| 2 | 3 | |||||
| 3 | 0 | |||||
| 4 | 0 | |||||
| 5 | 0 | |||||
| b | 2 | 2 | 0 | 1 | 0 |
Eine weitere Möglichkeit, die Fehlstände einer Permutation darzustellen, ist das Rothe-Diagramm (benannt nach Heinrich August Rothe). In einem Schema bestehend aus Feldern wird zunächst in jeder Zeile diejenige Spalte mit einem Punkt markiert, für die gilt. Diese Felder entsprechen gerade den Einträgen mit Wert der zugehörigen Permutationsmatrix. Die Fehlstände der Permutation entsprechen dann denjenigen Feldern, die sowohl einen Punkt unterhalb in der gleichen Spalte, als auch einen Punkt rechts in der gleichen Zeile haben. Diese Felder werden mit einem Kreuz markiert. Auf diese Weise wird ein Feld genau dann mit einem Kreuz markiert, wenn ein Fehlstand von ist.[1]
Aus dem Rothe-Diagramm lässt sich sowohl die Inversionstafel, als auch der Lehmer-Code ablesen. Die Zahl entspricht gerade der Anzahl der Kreuze in der Spalte und die Zahl der Anzahl der Kreuze in der Zeile . Transponiert man das Diagramm (vertauscht man also die Zeilen und Spalten), dann erhält man eine Darstellung der Fehlstände der zugehörigen inversen Permutation. Weist das Rothe-Diagramm einer Permutation im Feld ein Kreuz auf, dann gilt dies für das Diagramm der zugehörigen inversen Permutation im Feld . Aufgrund der Symmetrieeigenschaft des Rothe-Diagramms gilt demnach für die inverse Permutation[1]
- und .
Für selbstinverse Permutationen, also Permutationen, für die gilt, stimmen demnach Inversionstafel und Lehmer-Code überein.
Permutationsgraph
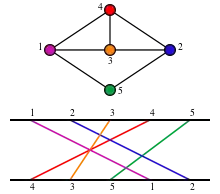
Jeder Permutation kann mit Hilfe der Fehlstände auch ein Permutationsgraph (nicht zu verwechseln mit der Graphdarstellung einer Permutation) zugeordnet werden. Der Permutationsgraph einer Permutation ist ein ungerichteter Graph mit der Knotenmenge
und der Kantenmenge
- .
Die Kanten des Permutationsgraphen verbinden also diejenigen Zahlenpaare, die einen Fehlstand erzeugen. Permutationsgraphen können auch geometrisch als Schnittgraphen der Strecken
für definiert werden. Die Endpunkte dieser Strecken liegen auf zwei parallelen Geraden und zwei Strecken schneiden sich genau dann, wenn die Zahlen an den Endpunkten einen Fehlstand erzeugen. Permutationsgraphen können auch dadurch charakterisiert werden, dass sowohl der Graph , als auch sein Komplementgraph Vergleichbarkeitsgraphen sind. Der Komplementgraph entspricht dabei dem Permutationsgraphen der reversen Permutation .
Beispiel
Beispielsweise besitzt der Permutationsgraph der Permutation die Kantenmenge
- .
Verwendung
Aufzählung von Permutationen
Fasst man die Inversionstafel beziehungsweise den Lehmer-Code als Zahl in einem fakultätsbasierten Zahlensystem auf, lässt sich jeder Permutation eine eindeutige Nummer in der Menge zuweisen. Aus der Inversionstafel erhält man so die Nummer
und aus dem Lehmer-Code die Nummer
- .
Diese beiden Nummern stimmen nur für selbstinverse Permutationen überein. Weitere Varianten zur Nummerierung von Permutationen bestehen durch die Betrachtung der Zahlenpaare, die in der Fehlstandsdefinition statt und/oder statt erfüllen. Diese Zahlenpaare entsprechen dann im Rothe-Diagramm Kreuzen rechts statt links beziehungsweise unterhalb statt oberhalb der Punkte. Die Vektoren bestehend aus den Summen der Kreuze pro Zeile oder Spalte können dann ebenfalls als Zahlen in einem fakultätsbasierten Zahlensystem aufgefasst werden.[6]
Beispiel
Für die Permutation erhält man aus der zugehörigen Inversionstafel die Nummer
und aus dem zugehörigen Lehmer-Code die Nummer
- .
Anordnung von Permutationen
.svg.png.webp)
Weiter lässt sich durch Betrachtung der Fehlstände auf der Menge der -stelligen Permutationen eine partielle Ordnung angeben. Eine solche Ordnungsrelation wird für Permutationen durch
definiert. Zwei Permutationen stehen dabei in Relation, wenn die Menge der Fehlstände der ersten Permutation eine Teilmenge der Fehlstandsmenge der zweiten Permutation ist. Das minimale Element bezüglich dieser Ordnung ist die identische Permutation, während das maximale Element diejenige Permutation ist, die die Reihenfolge aller Zahlen umkehrt.
Grafisch lässt sich diese Ordnungsrelation mit Hilfe eines Hasse-Diagramms veranschaulichen. Zwei Permutationen sind dabei durch eine Kante verbunden, wenn sie durch eine Nachbarvertauschung auseinander hervorgehen. Die Knoten und Kanten des Hasse-Diagramms bilden einen Cayley-Graphen, der isomorph zum Kantengraphen des entsprechenden Permutaeders ist.
Beispiel
In dem nebenstehenden Hasse-Diagramm der Permutationen der symmetrischen Gruppe befindet sich die bezüglich dieser Ordnung kleinste Permutation ganz unten und die größte Permutation ganz oben. Blaue, grüne und rote Kanten entsprechen jeweils den Nachbarvertauschungen , und , die von unten nach oben gesehen immer genau einen Fehlstand erzeugen.
Geschichte
Das Konzept des Fehlstands einer Permutation wurde im Jahr 1750 von Gabriel Cramer in seinem Werk Introduction à l’analyse des lignes courbes algébriques eingeführt. Im Rahmen der nach ihm benannten cramerschen Regel zur Angabe der Lösung linearer Gleichungssysteme definierte er die Determinante einer quadratischen Matrix durch
- ,
wobei die Summe über alle -stelligen Permutation läuft.[7] Die cramersche Regel war der Anstoß für die Entwicklung einer umfangreichen Determinantentheorie.
Für das Konzept des Fehlstands wurden im Lauf der Zeit verschiedene Begriffe verwendet. Cramer selbst bezeichnete Fehlstände als dérangement (Vertauschung), Pierre-Simon Laplace verwendete 1772 den Begriff variation (Veränderung) und Joseph Gergonne führte schließlich 1813 den Begriff inversion (Umkehrung) ein, der heute vor allem im englischsprachigen Raum verwendet wird.[8] Der deutsche Begriff „Fehlstand“ wurde Anfang des 20. Jahrhunderts von Gerhard Kowalewski popularisiert.[9]
Literatur
- Albrecht Beutelspacher: Lineare Algebra. Eine Einführung in die Wissenschaft der Vektoren, Abbildungen und Matrizen. 6. Auflage. Vieweg, 2009, ISBN 3-528-56508-X.
- Siegfried Bosch: Lineare Algebra. 4. überarbeitete Auflage. Springer, 2009, ISBN 3-540-76437-2.
- Donald E. Knuth: The Art of Computer Programming. 2. Auflage. Volume 3: Sorting and Searching. Addison-Wesley, 1998, ISBN 0-201-89685-0.
Weblinks
- Eric W. Weisstein: Permutation Inversion. In: MathWorld (englisch).
Einzelnachweise
- Donald E. Knuth: The Art of Computer Programming, Volume 3: Sorting and Searching. S. 14.
- Donald E. Knuth: The Art of Computer Programming, Volume 3: Sorting and Searching. S. 15.
- Donald E. Knuth: The Art of Computer Programming, Volume 3: Sorting and Searching. S. 16.
- Vladimir Nikolaevič Sačkov: Probabilistic Methods in Combinatorial Analysis. Cambridge University Press, 1997, S. 30.
- Donald E. Knuth: The Art of Computer Programming, Volume 3: Sorting and Searching. S. 13.
- Donald E. Knuth: The Art of Computer Programming, Volume 3: Sorting and Searching. S. 18.
- Thomas Muir: Theory of determinants in the historical order of development. Band 1. Macmillan and Co, 1906, S. 13.
- Thomas Muir: Theory of determinants in the historical order of development. Band 1. Macmillan and Co, 1906, S. 25,134.
- Gerhard Kowalewski: Einführung in die Determinantentheorie einschließlich der unendlichen und der Fredholmschen Determinanten. Veit & Co., 1909.