Hasse-Diagramm
In der Mathematik ist ein Hasse-Diagramm (auch Ordnungs- oder einfach Liniendiagramm genannt) eine bestimmte graphische Darstellung endlicher halbgeordneter Mengen. Solche Diagramme werden nach dem Mathematiker Helmut Hasse benannt.[1]
Das Hasse-Diagramm für eine Halbordnung ergibt sich als Darstellung eines gerichteten Graphen, wobei die Elemente von die Knoten bilden. Zwei Knoten und werden durch eine Kante verbunden, wenn gilt und es keinen Knoten gibt mit . (Hierbei ist als und zu verstehen.) Die Einschränkung auf solche nennt man transitive Reduktion der Halbordnung. Die Richtung der Kante wird dadurch zum Ausdruck gebracht, dass sich der Knoten oberhalb von befindet. Solch eine Anordnung lässt sich erreichen, da das Hasse-Diagramm zyklenfrei ist. Schleifen bei Reflexivität werden weggelassen.
Manchmal werden Hasse-Diagramme auch verwendet, um Striktordnungen (Ordnungsrelationen zweiter Art) darzustellen.
Beispiele
Teilerverband
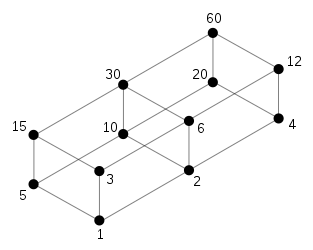
Die Teiler einer natürlichen Zahl lassen sich mittels eines Hasse-Diagramms darstellen, da sie bezüglich der Teilbarkeitsrelation eine halbgeordnete Menge, den Teilerverband, bilden. Das Diagramm heißt in diesem Falle auch Teilerbild. Das folgende Bild zeigt das Hasse-Diagramm der Teiler von 60.
Potenzmenge
Die -elementige Potenzmenge einer -elementigen Menge mit der Mengeninklusion lässt sich als Hasse-Diagramm darstellen. Dabei bilden die Elemente der Potenzmenge die Knoten und zwei Elemente sind durch eine Kante verbunden, wenn sie in einer Teilmengenrelation stehen. Die durch den untersten Knoten dargestellte leere Menge ist eine Teilmenge aller Elemente; das durch den obersten Knoten dargestellte Universum ist eine Obermenge aller Elemente.
Besonders übersichtlich und verbreitet ist die Anordnung der Mengen, die gleich viele Elemente enthalten, in derselben Ebene des Hasse-Diagramms. Ebenso ist es üblich und empfehlenswert, die Mengen in den Ebenen von links nach rechts lexikographisch zu ordnen.
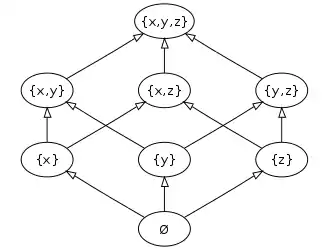
Ein kleines Beispiel für ein Hasse-Diagramm einer Potenzmenge liefert die Menge :
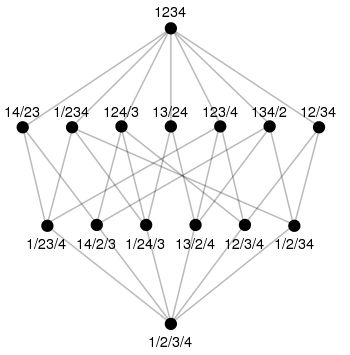
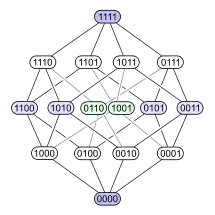
Ein etwas aufwändigeres Diagramm erhält man mit der sechzehnelementigen Potenzmenge einer vierelementigen Menge. Sie ist von besonderer Bedeutung für Aussagenlogik und Mengenlehre. Ihre in der beschriebenen Weise nächstliegende Darstellung ist die linke der drei Grafiken, die den rhombendodekaedrischen dreidimensionalen Schatten des vierdimensionalen Würfels zeigt. Die beiden anderen Grafiken rechts der rhombendodekaedrischen zeigen ebenfalls mögliche Hasse-Diagramme der Potenzmenge einer vierelementigen Menge, die für manche Zwecke besser geeignet sein können als die Schichtung nach der Anzahl der Elemente. Graphische Darstellungen, die für alle Zwecke gleichermaßen ideal sind, gibt es nicht. So müssen geeignete Hasse-Diagramme in der Auseinandersetzung mit einem bestimmten Thema oft erst gefunden werden.
 | 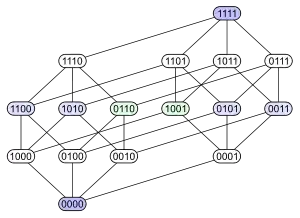 | 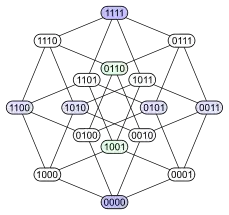 |
Weblinks
- Weisstein, Eric W.: Hasse Diagram. In: MathWorld (englisch).
- Video: Hassediagramme (Teil 1). Pädagogische Hochschule Heidelberg (PHHD) 2012, zur Verfügung gestellt von der Technischen Informationsbibliothek (TIB), doi:10.5446/19863.
Einzelnachweise
- Helmut Hasse: Über die Klassenzahl abelscher Zahlkörper. Akademie-Verlag, Berlin 1952, S. 137, Fußnote 2.