Bubblesort

Bubblesort (auch Sortieren durch Aufsteigen oder Austauschsortieren) ist ein Algorithmus, der vergleichsbasiert eine Liste von Elementen sortiert. Dieses Sortierverfahren arbeitet in-place, sortiert stabil und hat eine Laufzeit von $\Theta (n^{2})$ im schlimmsten Fall (Worst-Case) wie auch im durchschnittlichen Fall (Average-Case). Damit ist die Laufzeit asymptotisch nicht optimal. In der Praxis wird Bubblesort kaum eingesetzt, da andere Verfahren ein besseres Laufzeitverhalten haben. Der Algorithmus spielt allerdings in der Lehre eine Rolle, da er als einfach zu erklären bzw. zu demonstrieren gilt. Des Weiteren eignet sich der Algorithmus, um Techniken wie schrittweise Optimierungen, Laufzeit- bzw. Komplexitäts- und Korrektheitsanalyse einzuführen.

Visualisierung von Bubblesort

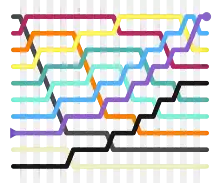
Prinzip

Bubblesort an einer Zahlenliste

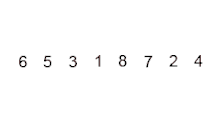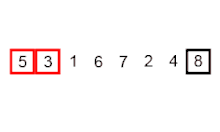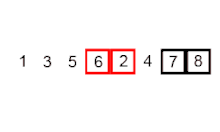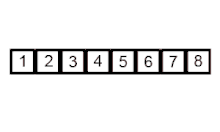
In der Bubble-Phase wird die Eingabe-Liste von links nach rechts durchlaufen. Dabei wird in jedem Schritt das aktuelle Element mit dem rechten Nachbarn verglichen. Falls die beiden Elemente das Sortierkriterium verletzen, werden sie getauscht. Am Ende der Phase steht bei auf- bzw. absteigender Sortierung das größte bzw. kleinste Element der Eingabe am Ende der Liste.

Die Bubble-Phase wird solange wiederholt, bis die Eingabeliste vollständig sortiert ist. Dabei muss das letzte Element des vorherigen Durchlaufs nicht mehr betrachtet werden, da die restliche zu sortierende Eingabe keine größeren bzw. kleineren Elemente mehr enthält.

Je nachdem, ob auf- oder absteigend sortiert wird, steigen die größeren oder kleineren Elemente wie Blasen im Wasser (daher der Name) immer weiter nach oben, das heißt, an das Ende der Liste. Es werden stets zwei Zahlen miteinander in „Bubbles“ vertauscht.

Algorithmus

Um die Darstellung des Algorithmus zu vereinfachen, wird im Folgenden als Vergleichsrelation $>$ (größer als) verwendet. Wie bei jedem auf Vergleichen basierenden Sortierverfahren kann diese auch durch eine andere Relation ersetzt werden, die eine totale Ordnung definiert.

Der Algorithmus in seiner einfachsten Form als Pseudocode:

bubbleSort(Array A)
  for (n=A.size; n>1; --n){
    for (i=0; i<n-1; ++i){
      if (A[i] > A[i+1]){
        A.swap(i, i+1)
      } // Ende if
    } // Ende innere for-Schleife
  } // Ende äußere for-Schleife

Die Eingabe ist in einem Array gespeichert. Die äußere Schleife verringert schrittweise die rechte Grenze für die Bubble-Phase, da nach jedem Bubblen an der rechtesten Position das größte Element der jeweils unsortierten Rest-Eingabe steht. In der inneren Schleife wird der noch nicht sortierte Teil des Feldes durchlaufen. Dabei werden zwei benachbarte Daten vertauscht, wenn sie in falscher Reihenfolge sind (also das Sortierkriterium verletzen).

Allerdings nutzt diese einfachste Variante nicht die Eigenschaft aus, dass nach einer Iteration, in der keine Vertauschungen stattfanden, auch in den restlichen Iterationen keine Vertauschungen mehr stattfinden. Der folgende Pseudocode berücksichtigt dies:

bubbleSort2(Array A)
  n = A.size
  do{
    swapped = false
    for (i=0; i<n-1; ++i){
      if (A[i] > A[i+1]){
        A.swap(i, i+1)
        swapped = true
      } // Ende if
    } // Ende for
    n = n-1
  } while (swapped)

Die äußere Schleife durchläuft die zu sortierenden Daten, bis keine Vertauschungen mehr notwendig sind.

Beispiel

Eine Reihe von fünf Zahlen soll aufsteigend sortiert werden.

Die fett gedruckten Zahlen werden jeweils verglichen. Ist die linke größer als die rechte, so werden beide vertauscht; das Zahlenpaar ist dann blau markiert. Im ersten Durchlauf wandert somit die größte Zahl ganz nach rechts. Der zweite Durchlauf braucht somit die letzte und vorletzte Position nicht mehr zu vergleichen. → Dritter Durchlauf: kein Vergleich letzte/vorletzte/vorvorletzte…

55 07 78 12 42 1. Durchlauf 07 55 78 12 42 07 55 78 12 42 07 55 12 78 42 Letzter Vergleich 07 55 12 42 78 2. Durchlauf 07 55 12 42 78 07 12 55 42 78 Letzter Vergleich 07 12 42 55 78 3. Durchlauf 07 12 42 55 78 Letzter Vergleich 07 12 42 55 78 4. Durchlauf + Letzter Vergleich 07 12 42 55 78 Fertig sortiert.

Komplexität

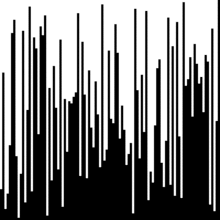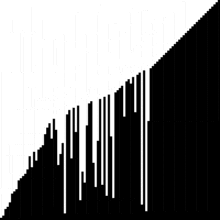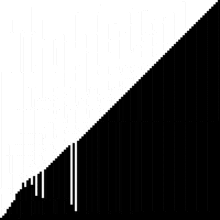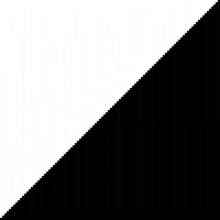
Beispiel, wie Bubblesort eine Liste sortiert. Die Listenelemente werden durch Balken dargestellt. Die x-Achse gibt an, wo sich ein Element in der Liste befindet; die Höhe gibt an, wie groß ein Element ist. Ein Frame entspricht einem Durchlauf.
(Animation starten)

Ungünstigster Fall

Bubblesort hat die Laufzeit ${\mathcal {O}}(n^{2})$ für Listen der Länge $n$ . Im Falle der umgekehrt sortierten Liste $(n,n-1,\dotsc ,2,1)$ werden maximal ${\tfrac {n\cdot (n-1)}{2}}$ viele Vertauschungen ausgeführt: um das erste (und größte) Element $n$ ganz nach rechts zu bewegen, werden $n-1$ Vertauschungen vorgenommen. Allgemein: Die Bewegung des $k$ -ten Elements an die Stelle $n$ wird durch $n-k$ Vertauschungen vollzogen. Aufsummieren über alle $k$ ergibt im Ganzen ${\tfrac {1}{2}}(n^{2}-n)\in {\mathcal {O}}(n^{2})$ Vertauschungen. Da nur Paare vertauscht werden, die auch vorher verglichen wurden, benötigt der Algorithmus auch mindestens ebenso viele Vergleiche. Betrachtet man den Pseudocode des Algorithmus, so sieht man leicht ein, dass keine der Anweisungen öfter als ${\tfrac {1}{2}}(n^{2}-n)$ -mal ausgeführt werden kann, also ist dies auch die bestmögliche untere Schranke.

Bester Fall

Bei einer bereits sortierten Liste wird Bubblesort die Liste nur einmal durchgehen, um festzustellen, dass die Liste bereits sortiert ist, weil keine benachbarten Elemente vertauscht werden mussten. Daher benötigt Bubblesort ${\mathcal {O}}(n)$ Schritte, um eine bereits sortierte Liste zu bearbeiten.

Falls die Elemente der Liste bereits nah den Stellen sind, die sie nach der Sortierung bekommen sollen, ist die Laufzeit erheblich besser als ${\mathcal {O}}(n^{2})$ .

Durchschnittlicher Fall

Die erwartete Anzahl der Vergleiche für eine zufällig gewählte Permutation der Liste $(1,2,\dotsc ,n)$ ist

{\frac {1}{2}}\left(n^{2}-n\cdot \ln n-(\gamma +\ln(2)-1)\cdot n\right)+{\mathcal {O}}({\sqrt {n}})

,

wobei $\gamma$ die Euler-Mascheroni-Konstante bezeichnet; die erwartete Anzahl der Vertauschungen beträgt ${\tfrac {1}{4}}(n^{2}-n)$ .[1]

Abgrenzung

Auch wenn Bubblesort nicht asymptotisch optimal ist, kann ein Einsatz für kleine Eingaben in Frage kommen, da für kleine $n$ die konstanten Laufzeitfaktoren eines Sortieralgorithmus dominieren, welche bei Bubblesort klein sind. Ein Anwendungsfall wäre die Verwendung von Bubblesort innerhalb eines rekursiv arbeitenden Sortierverfahrens, um die Anzahl an Rekursionen zu verringern.

Wenn die Elemente eines Feldes oder einer Liste (bis zu einer bestimmten Anzahl) mit einer hohen Wahrscheinlichkeit schon sortiert sind, eignet sich Bubblesort, da dies der Best-Case ist, in dem der Algorithmus eine lineare Laufzeit hat. Im Gegensatz dazu haben andere effiziente Sortierverfahren, wie z. B. Quicksort, oder asymptotisch optimale Verfahren, wie beispielsweise Mergesort, einen Best-Case von ${\mathcal {O}}(n\log n)$ .

Unter diesem Aspekt konkurriert Bubblesort mit Insertionsort, dessen Best-Case eine schon sortierte Folge ist und welches die gleiche Komplexität wie Bubblesort aufweist (wie auch im Average- und Worst-Case). Für beide Sortierverfahren gilt: Sie sind stabil und arbeiten in-place. Je nach Implementation hat Insertionsort jedoch geringere konstante Laufzeitfaktoren als Bubblesort.

Hasen und Schildkröten

Die Position der Elemente vor dem Sortieren ist entscheidend für den Sortieraufwand von Bubblesort. Große Elemente zu Beginn wirken sich nicht negativ aus, da sie schnell nach hinten getauscht werden; jedoch kleine Elemente am Ende bewegen sich nur langsam nach vorn. Deshalb bezeichnet man die schnell getauschten Elemente als Hasen und die langsamen als Schildkröten.

Combsort (oder auch Gapsort genannt) ist der schnellste auf Bubblesort beruhende Algorithmus. Im Unterschied zu Bubblesort werden hier weit voneinander entfernt liegende Elemente miteinander verglichen und vertauscht, um das Dilemma von langsam wandernden Elementen zu vermeiden. Seine Laufzeit liegt im Worst-Case ebenso bei ${\mathcal {O}}(n^{2})$ und im Best-Case bei ${\mathcal {O}}(n\log {\sqrt {(}}n))$ (Bubblesort: ${\mathcal {O}}(n)$ ). Damit erreicht Combsort im Worst- und im Best-Case die gleiche Komplexität wie Quicksort.

Cocktailsort (oder auch Shakersort genannt) ist ein alternierender Sortieralgorithmus, der die Elemente von der linken zur rechten Seite und von der rechten zur linken Seite wandern lässt. Damit wird ebenso dem Problem von nur langsam nach vorn wandernden Elementen entgegengewirkt. Aufgrund der Alternierung wird dieser Algorithmus auch Bidirectional-Bubblesort genannt. Im Worst-Case liegt seine Laufzeit, wie die von Bubblesort, in ${\mathcal {O}}(n^{2})$ .

Oyelami O.M. veröffentlichte im Jahr 2009 eine optimierte Version von Bubblesort, welche den Worst-Case für umgekehrt sortierte Felder/Listen vermeidet. Aufgrund der damit einhergehenden Sortierung über Distanz ist der von ihm verwendete Algorithmus nicht mehr stabil. In Anlehnung an das obige „bubbleSort3“ wird nachfolgend ein optimierter „bidirektionaler Bubblesort“ mittels „papyrus script function“ veranschaulicht. Float[] a ist dabei beispielhaft der Zeiger auf ein Array mit Fließkommazahlen. Die beiden integer-Parameter stellen den flexiblen Sortierbereich für das Array dar (Startwert „L“, Endwert „R“). Angenommen das Array hat 99 Elemente und beginnt bei 0, dann muss L=0 und R=98 gesetzt werden, um es vollständig zu sortieren.

 '''FUNCTION''' SortByBubble3(Float[] a, Int L, Int R)
 1
 2  float X  ; pivot element
 3  float f  ; temp element for swap
 4  int m  ; last swap position
 5  int i  ; counter
 6; ------------------------ round1: suggested by Oyelami
 7  i = L
 8  m = R
 9 '''WHILE''' (i < m) ; to avoid worst-case by using an array sorted in reverse order
 10  X = a[i]
 11  f = a[m]
 12  '''IF''' (X > f)
 13   a[m] = X
 14   a[i] = f
 15  '''ENDIF'''
 16  i = i + 1
 17  m = m - 1
 18 '''ENDWHILE'''
 19; ----------------------- round2: optimized bi-directional BubbleSort
 20 '''WHILE''' (L < R)
 21  X = a[L]
 22  m = L - 1    ; init "m" out of sorting range related to Left bound
 23  i = L + 1
 24  '''WHILE''' (i <= R) ; -- BottomUp loop -- sorts to maximum at the end
 25   f = a[i]
 26   '''IF''' (X <= f)
 27    X = f   ; no exchange: set "pivot" to follower element
 28   '''ELSE'''
 29    a[i] = X  ; \ swap two elements
 30    m = i - 1  ; - update "last swap" position
 31    a[m] = f  ; / and keep current "pivot" for next comparison
 32   '''ENDIF'''
 33   i = i + 1  ; i++
 34  '''ENDWHILE'''
 35;         -------------
 36  R = R - 1   ; R--
 37  '''IF''' (R > m)
 38   '''IF''' (L < m)
 39    R = m   ; shrink the Right bound as much as possible
 40   '''ELSE'''
 41    R = L ; no swap last time, break the loop!
 42   '''ENDIF'''
 43  '''ENDIF'''
 44;          ==============
 45  X = a[R]
 46  m = R + 1    ; init "m" out of sorting range related to Right bound
 47  i = R - 1
 48  '''WHILE''' (i >= L) ; -- TopDown loop -- sorts to minimum on start
 49   f = a[i]
 50   '''IF''' (X >= f)
 51    X = f   ; no exchange: set "pivot" to follower element
 52   '''ELSE'''
 53    a[i] = X  ; \ swap two elements
 54    m = i + 1  ; - update "last swap" position
 55    a[m] = f  ; / and keep current "pivot" for next comparison
 56   '''ENDIF'''
 57   i = i - 1  ; i--
 58  '''ENDWHILE'''
 59  L = L + 1   ; L++
 60  '''IF''' (L < m)
 61   '''IF''' (R > m)
 62    L = m
 63   '''ELSE'''
 64    L = R ; no swap last time, break the loop!
 65   '''ENDIF'''
 66  '''ENDIF'''
 67 '''ENDWHILE'''
 68 '''ENDFUNCTION'''

Literatur

Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein: Introduction to Algorithms. 2. Auflage. MIT Press, Cambridge MA 2001, ISBN 0-262-03293-7, S. 38.
Donald E. Knuth: The Art of Computer Programming: Volume 3 Sorting and Searching. 2. Auflage. Addison-Wesley, Reading MA 1997, ISBN 0-201-89685-0, S. 106–110.

Weblinks

Commons: Bubblesort – Sammlung von Bildern, Videos und Audiodateien

Einzelnachweise

Donald E. Knuth: The Art of Computer Programming: Volume 3 Sorting and Searching. 2. Auflage. Addison-Wesley, Reading MA 1997, ISBN 0-201-89685-0, S. 108–109.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Donald E. Knuth: The Art of Computer Programming: Volume 3 Sorting and Searching. 2. Auflage. Addison-Wesley, Reading MA 1997, ISBN 0-201-89685-0, S. 108–109.