Planetenschleife
Als Planetenschleife oder Oppositionsschleife bezeichnet man das Phänomen, dass jeder obere Planet (Mars bis Neptun) in den Monaten um seine Opposition, d. h. wenn er von der Erde aus gesehen mit der Sonne einen Winkel von 180° einschließt, am Sternhimmel scheinbar zurückwandert, um später seine rechtläufige Bahn wieder fortzusetzen. Dies passiert, weil die Erde auf der „Innenbahn“ schneller ist. Dadurch scheint der beobachtete Planet stillzustehen und seine Bewegungsrichtung sich dann umzukehren. Auch jeder untere Planet (Merkur und Venus) zeigt dieses Verhalten im Bereich seiner unteren Konjunktion, weil dieser dann die Erde überholt.
Im alten Babylon prognostizierte man die Rückwärtsbewegungen der Planeten durch Extrapolation ihrer früheren Bahnen. Im Hellenismus entwickelten Astronomen dann eine ausgefeilte Theorie der Planetenbewegungen, die sogenannte Epizykeltheorie, die eine sehr genaue Prognose von Planetenschleifen gestattete. In der frühen Neuzeit, im heliozentrischen System des Nicolaus Copernicus, wurden schließlich die Planetenschleifen etwa vom deutschen Astronomen Johann Gabriel Doppelmayr[1] auf eine Art erläutert, wie wir sie auch heute noch für richtig halten: Wenn einer der oberen Planeten der Sonne gegenübersteht (Fachausdruck: „in Opposition steht“), befindet sich die Erde zwischen ihm und der Sonne. Durch ihren schnelleren Umlauf überholt die Erde den entfernteren Planeten innen, sodass jener sich für einige Wochen scheinbar rückläufig („retrograd“) bewegt.
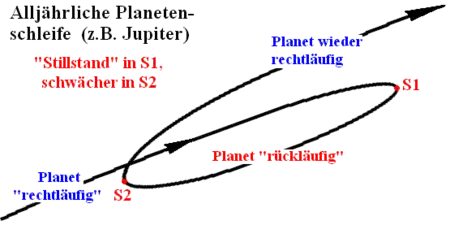
Wenn sich die Erde vor dem Überholen genau auf den Planeten zubewegt, scheint er einige Tage vor dem Hintergrund der Fixsterne stillzustehen (im Bild Punkt S1). Einige Monate später, nachdem die Erde den Planeten überholt hat, läuft sie vom Planeten weg, und ein zweiter Stillstand in S2 tritt ein.
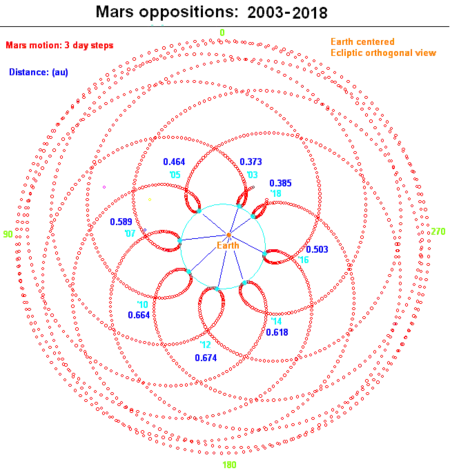
Diese Umkehrpunkte, in denen sich ein Planet für einige Tage fast nicht unter den Sternen weiterbewegt, nennt man „Stillstand“. Da aber die Bahnebenen der Planeten nicht exakt mit der Ekliptik zusammenfallen, handelt es sich streng genommen um Stillstände in ekliptikaler Länge. Änderungen der ekliptikalen Breite während des Stillstands verleihen der scheinbaren Bahn anstelle echter Umkehrpunkte eine Schleifenform. Solche Oppositionsschleifen lassen sich sehr gut bei Mars beobachten.
Wenn zwei Planeten in der Zeit um ihre Opposition dasselbe Sternbild durchwandern, kann es vorkommen, dass sich ihre Schleifen überlagern und sie sich nicht nur einmal, sondern dreimal begegnen; dies wird dreifache Konjunktion genannt. Alle paar Jahrhunderte tritt dies für Jupiter und Saturn ein. Es wird gelegentlich vermutet, dass ein solches Ereignis der Beschreibung des Sterns von Bethlehem im Neuen Testament zugrunde liegt. Matthäusevangelium Kap.2 könnte die Bemerkung, dass über Bethlehem „der Stern still stand“, genau darauf hindeuten, als die beiden Planeten ihren Lauf fast am selben Tag umdrehten. Diese Konstellation lässt sich auf das Jahr 7 v. Chr. zurückberechnen.
Solche Phänomene lassen sich mit 2D-Methoden in der Kurvendiskussion (zweidimensional), bzw. mit 3D-Methoden der Bahnbestimmung untersuchen. Bei einem solchen räumlichen Vorgang wird z. B. verständlich, dass sich die Erde in den Zeiten von S1 bzw. S2 vom anderen Planeten wegbewegt bzw. sich auf ihn zubewegt.
Konstruktion einer Planetenschleife
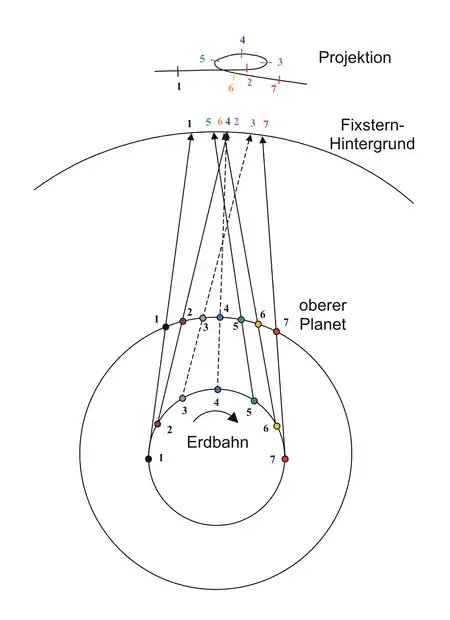
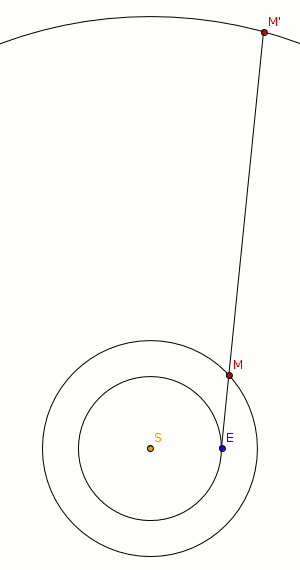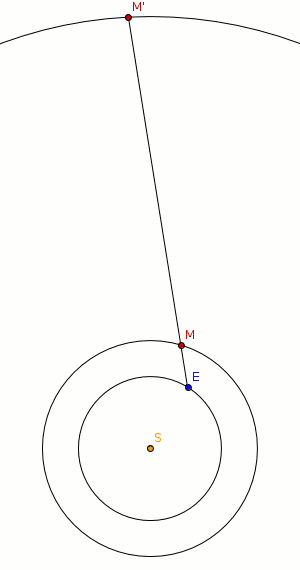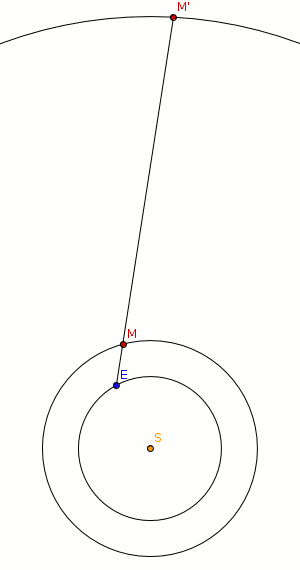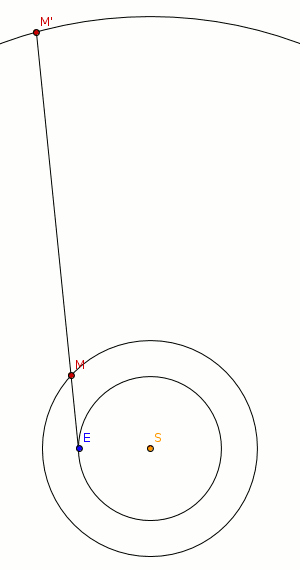
Die nebenstehende Abbildung zeigt die scheinbar schleifenförmige Bahn für die Bewegung des Beobachters auf der um die Sonne laufenden Erde. Die schleifenförmige Bahn ergibt sich durch eine Projektion der Bewegung des vergleichsweise nahen Planeten auf den Hintergrund der nahezu unendlich weit entfernten Fixsterne. Sie ergibt sich also durch die Parallaxe zwischen Erde, Planet und Fixstern-Hintergrund.
In einem halben Jahr legt die Erde die Wegstrecke von den Punkten 1 bis 7 zurück (siehe Abbildung unten). Im gleichen Zeitraum legt der weiter von der Sonne entfernte (d. h. obere) Planet wegen der geringeren mittleren Orbitalgeschwindigkeit eine kürzere Wegstrecke zurück, die zusätzlich aufgrund der größeren Entfernung deutlich weniger gekrümmt ist.
Verbindet man nun die Punkte zu den entsprechenden Zeitpunkten und verlängert den Strahl zum Fixstern-Hintergrund, ergibt sich scheinbar von den Punkten 1 bis 3 eine gleichlaufende von den Punkten 3 bis 5 eine rückläufige und von den Punkten 5 bis 7 wiederum eine gleichlaufende Bewegung. Die entsprechende Projektion auf den Fixstern-Hintergrund ergibt die schleifenförmige Bahn.
Selbstversuch
Den Effekt der scheinbaren Richtungsumkehr können zwei Personen im freien Gelände leicht nachstellen. Auf einem größeren freien Platz markiert man eine Stelle als Sonne (etwa mit einem Stein). In wenigen Metern Abstand von der Sonne läuft eine Person auf einer Kreisbahn um die Sonne. In einem Abstand von zum Beispiel 10 Metern läuft eine zweite Person deutlich langsamer auf einer Kreisbahn um die Sonne. Die innere Person blickt dann beim Gehen ständig auf die äußere. Dabei achtet die innere Person auch auf Objekte in großer Entfernung, etwa Bäume oder Türme. Für die innere Person wird dann beim Überholen der äußeren Person gut sichtbar, wie sich die äußere Person erst etwa auf einen Kirchturm zubewegt, sich dann rückwärts von ihm entfernt, um dann mit erhöhter Geschwindigkeit wieder auf ihn zuzulaufen.
Siehe auch
Einzelnachweise
- Johann Gabriel Doppelmayr: Planetenschlaufen, Atlas Novus Coelestis (Doppelmayer, 1742). In: AstroRara. Historische Astronomie interaktiv erleben. ETH-Bibliothek, 13. Dezember 2021, abgerufen am 13. Dezember 2021.
Weblinks
- Erklärung in Meyers Konversationslexikon, 4. Auflage, 1885–1892, Seite 108 und 109
- Demonstration retrograder Planetenbewegung (mit Mathematica)