Areasekans hyperbolicus und Areakosekans hyperbolicus

Areasekans hyperbolicus und Areakosekans hyperbolicus gehören zu den Areafunktionen. Sie sind die Umkehrfunktionen zu Sekans hyperbolicus bzw. Kosekans hyperbolicus. Als Funktionen werden sie ${\displaystyle \operatorname {arsech} }$ oder seltener ${\displaystyle \operatorname {sech} ^{-1}}$ bzw. ${\displaystyle \operatorname {arcsch} (x)}$ und seltener ${\displaystyle \operatorname {csch} ^{-1}(x)}$ geschrieben.

Definitionen

Man definiert d​en Areasekans hyperbolicus u​nd Areakosekans hyperbolicus m​eist über:

${\displaystyle \operatorname {arsech} (x)=\ln \left({\frac {1+{\sqrt {1-x^{2}}}}{x}}\right)}$

${\displaystyle \operatorname {arcsch} (x)=\ln \left({\frac {1+{\sqrt {1+x^{2}}}}{x}}\right)}$

Hierbei steht ${\displaystyle \ln }$ für den natürlichen Logarithmus.

Eigenschaften

Graph der Funktion Areasekans hyperbolicus

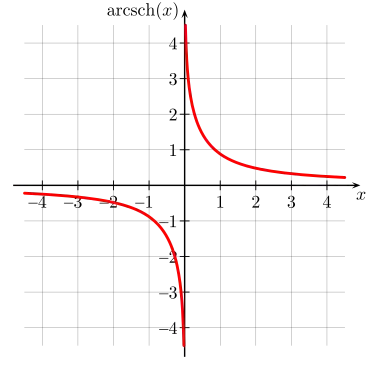Graph der Funktion Areakosekans hyperbolicus

	Areasecans hyperbolicus	Areakosekans hyperbolicus
Definitionsbereich	${\displaystyle 0<x\leq 1}$	${\displaystyle -\infty <x<+\infty \,;\,x\neq 0}$
Wertebereich	${\displaystyle 0\leq f(x)<+\infty }$	${\displaystyle -\infty <f(x)<+\infty \,;\,f(x)\neq 0}$
Periodizität	keine	keine
Monotonie	streng monoton fallend	${\displaystyle x\neq 0}$ streng monoton fallend
Symmetrien	keine	Ungerade Funktion ${\displaystyle f(x)=-f(-x)}$
Asymptote	${\displaystyle f(x)\to 0}$  ; ${\displaystyle x\to +1}$	${\displaystyle f(x)\to 0}$  ; ${\displaystyle x\to \pm \infty }$
Nullstellen	${\displaystyle x=1}$	keine
Sprungstellen	keine	keine
Polstellen	${\displaystyle x=0}$	${\displaystyle x=0}$
Extrema	keine	keine
Wendepunkte	${\displaystyle x={\frac {1}{2}}{\sqrt {2}}}$	keine

Spezielle Werte

Es gilt:

${\displaystyle \operatorname {arcsch} \,2=\ln \Phi }$

wobei ${\displaystyle \!\ \Phi }$ den goldenen Schnitt bezeichnet.

Reihenentwicklungen

${\displaystyle {\begin{alignedat}{2}\operatorname {arsech} (x)&=\ln \left({\frac {2}{x}}\right)-\sum _{k=1}^{\infty }{\frac {(2k-1)!!x^{2k}}{(2k)!!2k}}&\qquad \mathrm {f{\ddot {u}}r} \,0<x\leq 1\\\operatorname {arcsch} (x)&=\sum _{k=1}^{\infty }{\frac {P_{k-1}(0)}{k}}x^{k}\\&=\sum _{k=1}^{\infty }{\frac {(-1)^{k}\cdot ({\tfrac {1}{2}})_{k-1}}{(2k-1)(k-1)!}}\,x^{1-2k}\end{alignedat}}}$

Dabei ist ${\displaystyle P_{k}}$ das ${\displaystyle k}$-te Legendre-Polynom und ${\displaystyle ({\tfrac {1}{2}})_{n}}$ steht für das Pochhammer-Symbol.

Ableitungen

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}{\rm {arsech}}(x)=-{\frac {1}{x{\sqrt {1-x^{2}}}}}}$.

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\operatorname {arcsch} (x)=-{\frac {1}{|x|{\sqrt {1+x^{2}}}}}}$.

Integrale

Stammfunktionen d​es Areasekans hyperbolicus u​nd Areakosekans hyperbolicus sind:

${\displaystyle \int \operatorname {arsech} (x)\,\mathrm {d} x=x\cdot \operatorname {arsech} (x)-\arctan \left({\sqrt {{\frac {1}{x^{2}}}-1}}\right)+C}$

${\displaystyle \int \operatorname {arcsch} (x)\,\mathrm {d} x=x\cdot \operatorname {arcsch} (x)+\ln \left(x+x{\sqrt {1+{x}^{-2}}}\right)+C.}$

Umrechnung und Beziehungen zu anderen trigonometrischen Funktionen

${\displaystyle \operatorname {arsech} \,(x)=\operatorname {arcosh} \left({\frac {1}{x}}\right)}$

${\displaystyle \operatorname {arcsch} \,(x)=\operatorname {arsinh} \left({\frac {1}{x}}\right)}$

Siehe auch

• Trigonometrische Funktionen
• Kreis- und Hyperbelfunktionen

Weblinks

• Eric W. Weisstein: Inverse Hyperbolic Secant und Inverse Hyperbolic Cosecant auf MathWorld