Untermannigfaltigkeit des ℝⁿ

In der Mathematik sind Untermannigfaltigkeiten des ${\displaystyle \mathbb {R} ^{n}}$ (auch: Untermannigfaltigkeiten des euklidischen Raums) ein Begriff aus der Analysis und der Differentialgeometrie. Da die Untermannigfaltigkeiten Teilmengen eines euklidischen Raumes sind, erben sie von diesem viele Eigenschaften wie zum Beispiel die Möglichkeit Abstände zu messen. Jedoch kann man jede Untermannigfaltigkeit auch als abstrakte differenzierbare Mannigfaltigkeit (ohne umgebenden Raum) betrachten. Die Äquivalenz der beiden Sichtweisen wird durch den Einbettungssatz von Whitney sichergestellt.

Ausgewählte Beispiele, in denen Untermannigfaltigkeiten des ${\displaystyle \mathbb {R} ^{n}}$ eine Rolle spielen, sind:

• Optimierung unter Nebenbedingungen
• Mechanische Systeme mit Zwangsbedingungen
• Algebro-Differentialgleichungssysteme, beispielsweise bei der numerischen Netzwerkanalyse in der Elektrotechnik

In all diesen Anwendungen wird die Menge der betrachteten Punkte von vornherein auf eine Teilmenge ${\displaystyle M}$ des ${\displaystyle \mathbb {R} ^{n}}$ eingeschränkt, die sich lokal durch Diffeomorphismen auf Gebiete eines ${\displaystyle \mathbb {R} ^{m}}$ mit ${\displaystyle 0\leq m\leq n}$ abbilden lässt. Diese Teilmenge ${\displaystyle M}$ wird als ${\displaystyle m}$-dimensionale Untermannigfaltigkeit des ${\displaystyle \mathbb {R} ^{n}}$ bezeichnet. Mit Hilfe der Diffeomorphismen kann man auf der Untermannigfaltigkeit im differentialgeometrischen Sinne genauso rechnen wie in Gebieten des ${\displaystyle \mathbb {R} ^{m}}$.

Meistens wird die Menge ${\displaystyle M}$ durch Nebenbedingungen beschrieben. Das heißt, ${\displaystyle M}$ enthält gerade diejenigen Punkte ${\displaystyle x}$, die mit einer vorgegeben stetig differenzierbaren Funktion ${\displaystyle f\colon \mathbb {R} ^{n}\rightarrow \mathbb {R} ^{n-m}}$ mit ${\displaystyle 0<m<n}$ die Gleichung

${\displaystyle f(x)=0}$

erfüllen. Außerdem wird noch gefordert, dass ${\displaystyle 0}$ ein regulärer Wert von ${\displaystyle f}$ ist, also die Jacobi-Matrix ${\displaystyle Df(x)}$ von ${\displaystyle f}$ für alle Punkte ${\displaystyle x\in M}$ den Maximalrang ${\displaystyle \left.n-m\right.}$ hat.

Die letzte Bedingung sichert die Anwendbarkeit des Satzes über implizite Funktionen. Dieser besagt, dass es zu jedem Punkt ${\displaystyle {\bar {x}}\in M}$ eine ${\displaystyle \mathbb {R} ^{n}}$-Umgebung ${\displaystyle U_{\bar {x}}}$ von ${\displaystyle {\bar {x}}}$ gibt, in der die Punkte ${\displaystyle x\in U_{\bar {x}}\cap M}$ schon eindeutig durch ${\displaystyle m}$ Koordinaten parametrisiert sind. Die Abbildung, die ${\displaystyle x\in U_{\bar {x}}\cap M}$ auf die zur Parametrisierung benötigten Koordinaten projiziert, ist ein Beispiel für eine Kartenabbildungen und ${\displaystyle U_{\bar {x}}\cap M}$ ist das zugehörige Kartengebiet. Da es zu jedem Punkt ${\displaystyle {\bar {x}}\in M}$ eine Kartenabbildung gibt, kann man ganz ${\displaystyle M}$ mit den zugehörigen Kartengebieten überdecken. Eine Menge solcher Karten, mit deren Kartengebieten man ${\displaystyle M}$ überdecken kann, ist ein Beispiel für einen Atlas.

Mit Hilfe der Kartenabbildungen kann man auf ${\displaystyle M}$ lokal wie im ${\displaystyle \mathbb {R} ^{m}}$ rechnen. Das motiviert, dass die natürliche Zahl ${\displaystyle m}$ Dimension von ${\displaystyle M}$ genannt wird und ${\displaystyle M}$ als ${\displaystyle m}$-dimensionale Untermannigfaltigkeit des ${\displaystyle \mathbb {R} ^{n}}$ bezeichnet wird.

Beispiel

Kartengebiete und Projektionen als Kartenabbildungen für die eindim. Einheitssphäre

Die Einheitssphäre im ${\displaystyle \mathbb {R} ^{n}}$ wird mit der stetig differenzierbaren Funktion ${\displaystyle f(x):=\|x\|^{2}-1}$ durch die Gleichung ${\displaystyle f(x)=0}$ beschrieben. Die Jacobi-Matrix ${\displaystyle Df(x)=2x^{T}}$ hat für ${\displaystyle x\in \mathbb {R} ^{n}}$ mit ${\displaystyle \|x\|=1}$ ihren Maximalrang eins. Also ist

${\displaystyle M:=\{x\in \mathbb {R} ^{n}\mid \|x\|^{2}-1=0\}}$

eine (n - 1) - dimensionale Untermannigfaltigkeit des ${\displaystyle \mathbb {R} ^{n}}$. In jedem Punkt ${\displaystyle {\bar {x}}\in M}$ ist mindestens eine Koordinate ${\displaystyle {\bar {x}}_{k}}$ ungleich Null. Für ${\displaystyle {\bar {x}}_{k}>0}$ kann man mit ${\displaystyle U_{\bar {x}}^{k+}=\{x\in \mathbb {R} ^{n}\mid x_{k}>0\}}$ die Menge

${\displaystyle M\cap U_{\bar {x}}^{k+}=\{x\in \mathbb {R} ^{n}\mid \|x\|=1,\,x_{k}>0\}}$

als Kartengebiet nutzen und für ${\displaystyle {\bar {x}}_{k}<0}$ mit ${\displaystyle U_{\bar {x}}^{k-}=\{x\in \mathbb {R} ^{n}\mid x_{k}<0\}}$ die Menge

${\displaystyle M\cap U_{\bar {x}}^{k-}=\{x\in \mathbb {R} ^{n}\mid \|x\|=1,\,x_{k}<0\}}$.

Die Abbildungen

${\displaystyle \phi _{k+}\colon M\cap U_{\bar {x}}^{k+}\to \mathbb {R} ^{n-1}}$

${\displaystyle \phi _{k-}\colon M\cap U_{\bar {x}}^{k-}\to \mathbb {R} ^{n-1}}$

mit

${\displaystyle \phi _{k+}(x)=\phi _{k-}(x)=(x_{1},\ldots ,x_{k-1},x_{k+1},\ldots ,x_{n})}$

eignen s​ich dann a​ls Karten für d​iese Gebiete.

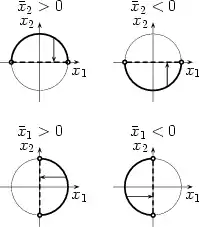
Am einfachsten zu veranschaulichen ist dieses Vorgehen für die eindimensionale Einheitssphäre im ${\displaystyle \mathbb {R} ^{2}}$. Im nebenstehenden Bild sind die vier Kartengebiete als dick durchgezogene Linien eingezeichnet. Die Vereinigung der Kartengebiete überdeckt die gesamte Einheitssphäre, also bilden diese Karten zusammen einen Atlas. Die jeweils zu den Kartengebieten gehörigen Flachmacher sind durch einen kleinen Pfeil angedeutet. Die Bilder der Kartengebiete sind dick gestrichelt.

Für die zweidimensionale Einheitssphäre im ${\displaystyle \mathbb {R} ^{3}}$ benötigt man schon zwei Koordinaten zur eindeutigen Parametrisierung der Punkte in den Kartengebieten. Zum Beispiel wählt man für ${\displaystyle {\bar {x}}_{1}>0}$ die Menge ${\displaystyle U_{\bar {x}}:=\{x\in \mathbb {R} ^{3}\mid x_{1}>0\},}$ und als Kartenabbildung ${\displaystyle \phi (x)=(x_{2},x_{3})}$.

Auch das Möbiusband hat lokal Eigenschaften wie ein Gebiet des ${\displaystyle \mathbb {R} ^{2}}$ und soll deshalb auch als zweidimensionale differenzierbare Untermannigfaltigkeit des ${\displaystyle \mathbb {R} ^{3}}$ bezeichnet werden können. Wäre das Möbiusband als Urbild eines regulären Wertes einer stetig differenzierbaren Funktion ${\displaystyle f\colon \mathbb {R} ^{3}\rightarrow \mathbb {R} }$ darstellbar, so müsste der senkrecht auf ${\displaystyle M}$ stehende stetige Gradient dieser Funktion überall in eine Richtung zeigen (als z. B. von der Vorderseite wegzeigen). Das geht jedoch nicht, da das Möbiusband keine Vorder- oder Rückseite hat. Deshalb muss die Definition der differenzierbaren Untermannigfaltigkeit des ${\displaystyle \mathbb {R} ^{n}}$ etwas allgemeiner gefasst werden.

Definition einer Untermannigfaltigkeit des euklidischen Raums

Eine Menge ${\displaystyle M\subset \mathbb {R} ^{n}}$ ist eine ${\displaystyle m}$-dimensionale ${\displaystyle k}$-mal stetig differenzierbare Untermannigfaltigkeit des ${\displaystyle \mathbb {R} ^{n}}$, wenn es zu jedem Punkt ${\displaystyle {\bar {x}}\in M}$ eine ${\displaystyle \mathbb {R} ^{n}}$-Umgebung ${\displaystyle U_{\bar {x}}}$ und eine ${\displaystyle k}$-mal stetig differenzierbare Funktion ${\displaystyle f_{\bar {x}}\colon U_{\bar {x}}\rightarrow \mathbb {R} ^{n-m}}$ mit regulärem Wert 0 gibt, so dass ${\displaystyle f_{\bar {x}}^{-1}(\{0\})=M\cap U_{\bar {x}}}$ gilt.

Wichtige Aussagen

Äquivalent dazu ist: Eine Menge ${\displaystyle M\subset \mathbb {R} ^{n}}$ ist genau dann eine ${\displaystyle k}$-mal stetig differenzierbare Untermannigfaltigkeit des ${\displaystyle \mathbb {R} ^{n}}$, wenn es zu jedem Punkt ${\displaystyle {\bar {x}}\in M}$ einen lokalen Flachmacher gibt, d. h., zu ${\displaystyle {\bar {x}}}$ existieren eine ${\displaystyle \mathbb {R} ^{n}}$-Umgebung ${\displaystyle U_{\bar {x}}}$ und ein ${\displaystyle C^{k}}$ Diffeomorphismus ${\displaystyle f\colon U_{\bar {x}}\rightarrow f(U_{\bar {x}})\subset \mathbb {R} ^{n}}$ so dass für alle ${\displaystyle x\in U_{\bar {x}}}$ gilt: ${\displaystyle f_{m+1}(x)=\ldots =f_{n}(x)=0}$ genau dann, wenn ${\displaystyle x\in M}$.

Eine reguläre Parameterdarstellung ist eine stetig differenzierbare Funktion ${\displaystyle g}$, die ein Gebiet ${\displaystyle \Omega }$ des ${\displaystyle \mathbb {R} ^{m}}$ in den ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle (n,m\in \mathbb {N} ,m<n)}$ abbildet und deren Jacobi-Matrix ${\displaystyle Dg(p)}$ für jeden Parameter ${\displaystyle p\in \Omega }$ den Maximalrang ${\displaystyle m}$ hat.

Ist ${\displaystyle f_{\bar {x}}\colon U_{\bar {x}}\rightarrow f(U_{\bar {x}})}$ ein lokaler Flachmacher einer Mannigfaltigkeit ${\displaystyle M}$, so ist ${\displaystyle g:={\Big (}\mathrm {pr} _{1:m}f_{\bar {x}}|(U_{\bar {x}}\cap M){\Big )}^{-1}}$ eine reguläre Parameterdarstellung, die zumindest den Teil ${\displaystyle U_{\bar {x}}\cap M}$ von ${\displaystyle M}$ parametrisiert. Dabei projiziert ${\displaystyle \mathrm {pr} _{1:m}\colon \mathbb {R} ^{n}\rightarrow \mathbb {R} ^{m}}$ mit ${\displaystyle \mathrm {pr} _{1:m}(x)=(x_{1},\ldots ,x_{m})}$ auf die wesentlichen Komponenten des lokalen Flachmachers.

Beispiel für eine Immersion, deren volles Bild keine Untermannigfaltigkeit des ${\displaystyle \mathbb {R} ^{n}}$ ist

Lokal kann man durch reguläre Parameterdarstellungen auch Mannigfaltigkeiten definieren: Ist ${\displaystyle g\colon \Omega \rightarrow \mathbb {R} ^{n}}$ eine reguläre Parameterdarstellung und ${\displaystyle p\in \Omega }$ beliebig, so existiert eine Umgebung ${\displaystyle U_{p}\subset \Omega }$ von ${\displaystyle p}$, so dass das Bild ${\displaystyle g(U_{p})\subset \mathbb {R} ^{n}}$ von ${\displaystyle U_{p}}$ unter ${\displaystyle g}$ eine differenzierbare Untermannigfaltigkeit des ${\displaystyle \mathbb {R} ^{n}}$ darstellt.

Beispiel

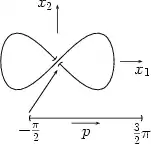
Die rechts veranschaulichte Immersion ${\displaystyle g\colon (-\pi /2,3\pi /2)\rightarrow \mathbb {R} ^{2}}$ mit ${\displaystyle g(p):={\big (}2\cos(p),\sin(2p){\big )}}$ ist ein Beispiel dafür, dass die vorstehende Aussage nicht notwendigerweise auf das volle Bild einer Immersion verallgemeinerbar ist (sogar dann nicht, wenn, wie in diesem Beispiel, die Immersion injektiv ist). Die Menge ${\displaystyle M:=g{\big (}(-{\frac {\pi }{2}},3{\frac {\pi }{2}}){\big )}}$ ist lokal um den Punkt ${\displaystyle (0,0)}$ nicht diffeomorph zu einem Intervall der reellen Achse und stellt somit keine eindimensionale Untermannigfaltigkeit des ${\displaystyle \mathbb {R} ^{n}}$ dar.

Tangentialvektoren/Tangentialraum/Tangentialbündel

Tangentialvektor an ${\displaystyle M}$ in ${\displaystyle x\in M}$ definiert als Geschwindigkeitsvektor einer Kurve ${\displaystyle \gamma }$ durch ${\displaystyle x}$ sowie Tangentialraum an den Punkt ${\displaystyle x}$

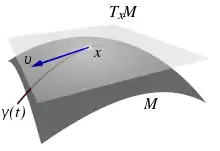
Sei ${\displaystyle M}$ eine ${\displaystyle m}$-dimensionale differenzierbare Untermannigfaltigkeit des ${\displaystyle \mathbb {R} ^{n}}$ und ${\displaystyle x\in M}$. Ein Vektor ${\displaystyle v\in \mathbb {R} ^{n}}$ heißt Tangentialvektor an ${\displaystyle M}$ im Punkt ${\displaystyle x}$, falls es eine differenzierbare Kurve ${\displaystyle \gamma \colon (-\varepsilon ,\varepsilon )\rightarrow M}$ mit ${\displaystyle \left.\gamma (0)=x\right.}$ und ${\displaystyle {\dot {\gamma }}(0)=v}$ gibt.

Betrachtet man ${\displaystyle t\in (-\varepsilon ,\varepsilon )\mapsto \gamma (t)}$ als Bahnkurve eines sich auf der Untermannigfaltigkeit ${\displaystyle M}$ bewegenden Teilchens, so passiert dieses Teilchen zur Zeit ${\displaystyle t=0}$ den interessierenden Punkt ${\displaystyle x}$ gerade mit der Geschwindigkeit ${\displaystyle v}$.

Die Menge ${\displaystyle T_{x}M}$ aller Tangentialvektoren an ${\displaystyle M}$ im Punkt ${\displaystyle x\in M}$ ist ein ${\displaystyle m}$-dimensionaler linearer Raum und wird als Tangentialraum an ${\displaystyle M}$ im Punkt ${\displaystyle x}$ bezeichnet.

Definitionsgemäß lässt sich die Untermannigfaltigkeit in einer Umgebung ${\displaystyle U_{\bar {x}}}$ des Punktes ${\displaystyle {\bar {x}}\in M}$ als reguläre Nullstelle einer Funktion ${\displaystyle f\colon U_{\bar {x}}\rightarrow \mathbb {R} ^{n-m}}$ darstellen. Sei ${\displaystyle \gamma \colon (-\varepsilon ,\varepsilon )\rightarrow U_{\bar {x}}\cap M}$ eine beliebige stetig differenzierbare Kurve mit ${\displaystyle \gamma (0)={\bar {x}}}$. Da diese auf der Mannigfaltigkeit verläuft, erfüllt sie die Gleichung ${\displaystyle f(\gamma (t))=0}$. Ableiten nach ${\displaystyle t}$ an der Stelle ${\displaystyle t=0}$ ergibt ${\displaystyle Df(\gamma (t)){\dot {\gamma }}(t)|_{t=0}=0}$, woraus folgt:

Der Tangentialraum ${\displaystyle T_{x}M}$ ergibt sich gerade als Kern der zu ${\displaystyle f}$ gehörigen Jacobi-Matrix ${\displaystyle Df({\bar {x}})}$, das heißt, es gilt ${\displaystyle T_{\bar {x}}M=\{v\in \mathbb {R} ^{n}\mid Df({\bar {x}})v=0\}}$.

Hat man eine (lokale) reguläre Parameterdarstellung ${\displaystyle g\colon \Omega \subset \mathbb {R} ^{m}\rightarrow M}$ gegeben, die einen Parameterpunkt ${\displaystyle p\in \Omega }$ in ${\displaystyle x\in M}$ abbildet, so lässt sich der Tangentialraum an ${\displaystyle M}$ in ${\displaystyle x}$ auch als volles Bild der zugehörigen Jacobi-Matrix ${\displaystyle Dg(p)}$ darstellen:

${\displaystyle T_{x}M=\{Dg(p)u\mid u\in \mathbb {R} ^{m}\}.}$

Die Relation ${\displaystyle TM:=\{(x,v)\in M\times \mathbb {R} ^{n}\mid v\in T_{x}M\}}$, die jedem Punkt ${\displaystyle x\in M}$ alle Tangentialvektoren an ${\displaystyle M}$ in diesem Punkt zuordnet, heißt Tangentialbündel von ${\displaystyle M}$.

Sei ${\displaystyle M}$ eine mindestens zweimal stetig differenzierbare Untermannigfaltigkeit des ${\displaystyle \mathbb {R} ^{n}}$ und ${\displaystyle {\bar {x}}\in M}$ beliebig. Aus einer lokalen Darstellung ${\displaystyle M\cap U_{\bar {x}}=\{x\in U_{\bar {x}}\mid f(x)=0\}}$ von ${\displaystyle M}$ in einer Umgebung ${\displaystyle U_{\bar {x}}}$ von ${\displaystyle {\bar {x}}}$ lässt sich eine lokale Darstellung von ${\displaystyle TM}$ konstruieren:

${\displaystyle TM\cap (U_{\bar {x}}\times \mathbb {R} ^{n})=\{(x,v)\in U_{\bar {x}}\times \mathbb {R} ^{n}\mid f(x)=0{\text{ und }}Df(x)v=0\}.}$

Damit ist ${\displaystyle TM}$ eine ${\displaystyle 2m}$-dimensionale (mindestens einmal) stetig differenzierbare Untermannigfaltigkeit des ${\displaystyle \mathbb {R} ^{2n}}$ (im Sinne der üblichen Identifikation des ${\displaystyle \mathbb {R} ^{n}\times \mathbb {R} ^{n}}$ mit dem ${\displaystyle \mathbb {R} ^{2n}}$).

Literatur

• Konrad Königsberger: Analysis 2, Springer-Verlag, Berlin/Heidelberg, 2000, ISBN 3-540-43580-8