Transformationskurve

Die Transformationskurve, auch Produktionsmöglichkeitenkurve oder Kapazitätslinie, ist in der Volkswirtschaftslehre die grafische Darstellung aller effizienten Gütermengenkombinationen bei gegebenem Ressourcen-Einsatz. Sie ist ein wirtschaftswissenschaftliches Instrument, das dazu dient, das grundsätzlich bestehende Problem der Knappheit und die daraus entstehenden Alternativen aufzuzeigen.

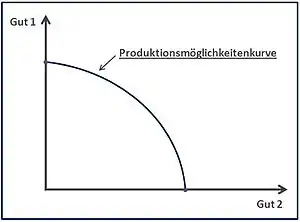
Abb. 1: Produktionsmöglichkeitenkurve

Die Realität wird im Modell der Produktionsmöglichkeiten stark vereinfacht anhand von zwei Gütern oder zwei Produktionsfaktoren dargestellt. Jedoch können Konzept, Erkenntnisse und Ergebnisse ohne Schwierigkeiten auf viele Güter und ganze Volkswirtschaften übertragen werden.[1]

Die geschlossene Menge unter der Transformationskurve wird Produktionsraum oder Produktionsmöglichkeitenmenge genannt. Er enthält alle möglichen Güterkombinationen, die mit den vorhandenen Produktionsfaktoren produziert werden können – allerdings weniger effizient als genau auf der Transformationskurve.

Einordnung und Beschreibung

Sowohl in der Betriebswirtschaftslehre als auch in der Volkswirtschaftslehre stellt die Transformationskurve ein wichtiges Werkzeug dar, um verschiedene Alternativen der Produktionsmöglichkeiten abzubilden. Dabei findet die Transformationskurve vor allem in der volkswirtschaftlichen Außenhandelstheorie besondere Bedeutung. Hierbei dient die Kurve als Grundlage für weitere Theorien und Modelle, wie das Ricardo-Modell, Heckscher-Ohlin-Modell oder das Rybczynski-Theorem. Die Tatsache, dass die in einer Volkswirtschaft jeweils verfügbaren Produktionsfaktoren wegen ihrer Knappheit nur wahlweise für die eine oder die andere Verwendung eingesetzt werden können, dass demnach – bei gegebener Produktionstechnik – das Produktionspotenzial begrenzt ist, begründet die Notwendigkeit des Instruments der Transformationskurve. Die Kurve könnte man daher auch als den geometrischen Ort aller maximal möglichen Mengenkombinationen von Gütern, Gütergruppen oder Produktionsfaktoren bezeichnen.[2] Im Modell der Transformationskurve wird dabei angenommen, dass alle Ressourcen vollständig in Anspruch genommen und nach dem ökonomischen Prinzip eingesetzt wurden.[3]

Aufgrund der Annahme von Knappheit oder Vollauslastung müssen sowohl in einem Unternehmen als auch in einer Volkswirtschaft Wahlentscheidungen getroffen werden, um eine alternative Gütermengenkombination oder Produktionsfaktorenkombination festzulegen. Eine Entscheidung zu treffen bedeutet immer auch, einen Verzicht in Kauf zu nehmen. Diesen Verzicht, genauer den Nutzenentgang, nennt man Opportunitätskosten oder auch Kosten der zweitbesten Alternative. Bei einer Bewegung entlang der Transformationskurve kommt es daher zu einem Zuwachs der Menge des einen Gutes, aber gleichzeitig auch zum Verzicht auf eine entsprechende Menge des anderen Gutes.[4]

Die Achsen des Produktionsmöglichkeitendiagramms können Mengen von Gütern (bspw. Brot oder Maschinen), Gütergruppen (bspw. Konsum- oder Investitionsgüter), Produktionsfaktoren (bspw. Arbeit oder Kapital) sowie sonstigen wirtschaftlichen Einheiten abbilden. In der folgenden Betrachtung soll aus Vereinfachungsgründen von einem Zwei-Güter-Fall ausgegangen werden.

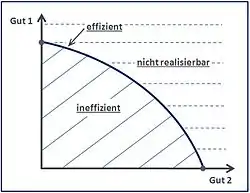
Abb. 2: Effizienzbereiche und Realisierungsmöglichkeiten im Modell

In der Literatur wird die Kurve zum Teil auch als Produktionsmöglichkeitengrenze bezeichnet.[5] Gemeint ist damit die Beschränkung der möglichen Produktionsmenge, die durch die Transformationskurve gesetzt wird.[1] Bezogen auf die Grafik (Abb. 2) bedeutet dies, dass nur diejenigen Güterkombinationen unterhalb bzw. links von und auf der Kurve möglich sind. Alle außerhalb dieses Bereichs liegenden Mengenkombinationen sind bei gleichbleibendem Stand von Technik, Wissen und Produktivität nicht realisierbar. Eine Ausnahme kann eine Volkswirtschaft im internationalen Handel aufzeigen. So kann es durch einen komparativen Vorteil dieser Volkswirtschaft möglich sein, eine Kombination außerhalb bzw. rechts von der Produktionsmöglichkeitenkurve zu erreichen.[6] Generell verschiebt sich die Transformationskurve dagegen nach außen und es werden somit bisher unerreichbare Mengenkombinationen realisierbar, wenn langfristig technisches Wissen und/oder Faktorausstattung wachsen. Die damit zusammenhängenden Fragen sind Gegenstand der Wachstumstheorie.[7] Des Weiteren kann anhand der Kurve die Effizienz beurteilt werden. Effizienz liegt vor, wenn alle Ressourcen vollständig genutzt sind.[8] Nur die Kombinationen von Gütermengen auf der Kurve können daher als effizient bezeichnet werden. Dagegen gelten alle Mengenzusammensetzungen unterhalb der Funktion als ineffizient, weil bei gleichem Faktoreinsatz mehr von einem der beiden Güter produziert werden könnte. Eine weitere denkbare Erklärung ist, dass die mögliche produktive Leistung nicht in dem Umfang genutzt wird, wie es beim gegebenen Stand des Wissens möglich gewesen wäre. Mit diesem Problem befassen sich die Preistheorie und Allokationstheorie.[7]

Lage und Gestalt der Kurve

Wie in Abb. 3 zu erkennen, unterscheidet man grundsätzlich zwischen zwei Arten des Verlaufs von Produktionsmöglichkeitskurven, der linear und der konkav zum Ursprung verlaufenden. Der in Abb. 3 a) dargestellte lineare Verlauf der Kurve wird durch die zugrunde liegenden Produktionsfunktionen bestimmt. Unabhängig vom Produktionsniveau wird dabei eine konstante Faktormenge pro Produkteinheit bei den beiden Gütern beansprucht. Ist diese Bedingung nicht erfüllt, nimmt die Transformationskurve in der Regel – wie in Abb. 3 b) zu erkennen – einen konkaven, also einen nach außen gekrümmten Verlauf an. Produktionsfunktion, Faktorintensität sowie die Produktionselastizität bestimmen also die Gestalt der Kapazitätslinie. Dabei haben ungleiche Elastizitäten und/oder unterschiedliche Faktorintensitäten eine Konkavität der Funktion zur Folge.[9]

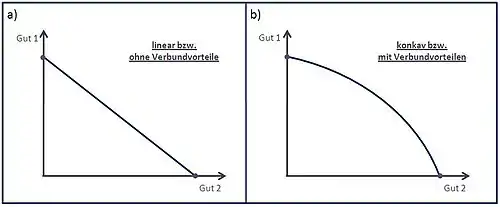
Abb. 3: linearer und konkaver Verlauf der Transformationskurve

Ein alternativ verständlicher und praxisorientierter Ansatz zur Art der Gestalt der Transformationskurve ist die Betrachtung der Verbundvorteile bei der Produktion. Nimmt man auf den Zwei-Güter-Fall bezogen an, dass mit der kombinierten Erzeugung der beiden Güter gegenüber einer separaten Produktion gewisse Verbundvorteile einhergehen, wird die Kurve einen konkaven Verlauf annehmen. Verbundvorteile meinen eine Ersparnis an zur Herstellung notwendigen Produktionsfaktoren. In der Praxis könnte die zusammengelegte Produktion zweier Güter beispielsweise zur Reduzierung der Verwaltungskosten oder dem Einkaufspreis gemeinsam verwendeter Rohstoffe aufgrund von Mengenrabatt bedeuten. Sollten sich dagegen aus der kombinierten Herstellung der Güter keine Verbundvorteile ergeben, wird die Produktionsmöglichkeitenkurve einen linearen Verlauf annehmen.[10]

In der Theorie sind zudem konvexe oder auch linear aus mehreren Teilstücken bestehende Verläufe denkbar. Die zusammengesetzte lineare Variante wird verursacht, wenn die Faktorintensitäten von zwei Gütern mit linear limitationalen Produktionsfunktionen ungleich sind.[11] Konvexität kann aufgrund Überlinearität einer Produktionsfunktion oder aus Negativwirkung bei kombinierter Produktion folgen.[12] Negativwirkung bedeutet in dem Fall, dass bei zusammengelegter Herstellung Nachteile wie höhere Kosten im Gegensatz zur getrennten Erzeugung der Güter entstehen.

Steigung – Grenzrate der Transformation

Die Steigung der Produktionsmöglichkeitenkurve, auch als Grenzrate der Transformation bezeichnet, weist typischerweise eine negative Steigung, also einen von links oben nach rechts unten fallenden Verlauf auf (siehe Abb. 3a). Die Opportunitätskosten – der unvermeidbare Verzicht auf eine bestimmte Menge des einen Gutes beim Produzieren einer zusätzlichen Mengeneinheit des anderen Gutes – erklären die fallende Steigung der Kurve. Das bedeutet, zwischen den in der Abbildung 3 dargestellten Gütern X und Y besteht eine inverse Beziehung, man könnte dies auch als einen „Trade-off“ zwischen den Gütern bezeichnen.[13] Mathematisch betrachtet entspricht die Grenzrate der Transformation dem Transformationsverhältnis, folglich dem Verhältnis der beiden Produktmengenänderungen von Gut X und Gut Y unter Verwendung deren Differentiale $\mathrm {d} x$ und $\mathrm {d} y$ .[14] Als Formel betrachtet ergibt sich:

GRT=-{\frac {\mathrm {d} y}{\mathrm {d} x}}

.

$GRT$ : Grenzrate der Transformation
$\mathrm {d}$ : Differential

Um für die Grenzrate einen positiven Betrag zu erhalten, wird vor das Verhältnis ein Negativzeichen gesetzt. Zugleich gibt dieses Verhältnis die marginalen Verzichts- bzw. Alternativkosten an.

Bei einer linearen Funktion bleibt das Transformationsverhältnis den kompletten Verlauf über unverändert, es liegen also konstante Alternativkosten vor. Bezogen auf den Zwei-Güter-Fall hätten beide Güter stets relative Kosten im gleichen Verhältnis, das heißt, sie wären in jedem Punkt auf der Funktion im gleichbleibenden Verhältnis der Grenzrate der Transformation substituierbar.

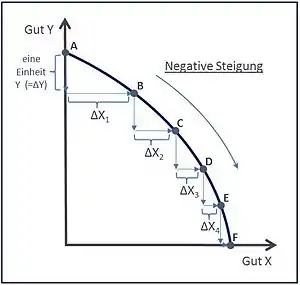
Abb. 4: Steigung – Grenzrate der Transformation

Vielfach tritt jedoch der in Abb. 3b beschriebene Fall der nach außen gekrümmten (= konkaven) Produktionsmöglichkeitenkurve auf. Hierbei verändert sich der Betrag der Steigung entlang des fallenden Verlaufs der Funktion degressiv. Grund dafür ist das „Gesetz der abnehmenden Alternativkosten“ in Verbindung mit dem Ertragsgesetz (= „Gesetz vom abnehmenden Ertragszuwachs“).[15] Dabei wird angenommen, dass die Erträge durch zusätzlichen Input geringer werden, je mehr Faktorleistung in einer bestimmten Produktion bereits vorhanden ist.[16] In Abb. 4 ist das Ertragsgesetz grafisch zu erkennen, verzichtet man auf eine Einheit des Gut Y, kann man ∆X1 Einheiten mehr von Gut X produzieren – das ist gleichzusetzen mit einem Ertrag in Höhe von ∆X1, bei einem Verzicht auf eine Einheit von Gut Y. Wird nun auf weitere Einheiten von Gut Y verzichtet, so nehmen die Erträge (in der Grafik ∆X2 … ∆X4) kontinuierlich ab. Ein möglicher Grund dafür ist, dass je mehr Produktionsfaktoren für die Herstellung des Gut X aus der Herstellung des Gut Y abgezogen werden, diese sich dabei umso weniger eignen für die zusätzliche Produktion von Gut X. Auch denkbar wäre, dass eines der beiden Produkte konstante und das andere Produkt sinkende Skalenerträge aufweist oder beide Produkte sinkende Skalenerträge aufweisen.[17] Im Zwei-Güter-Fall hätten beide Güter entlang der Kurve stets relative Kosten in einem differenten Verhältnis, das heißt, sie wären in jedem Punkt auf der Funktion im jeweiligen Verhältnis der Grenzrate der Transformation substituierbar.

Herleitung

Grafische Herleitung

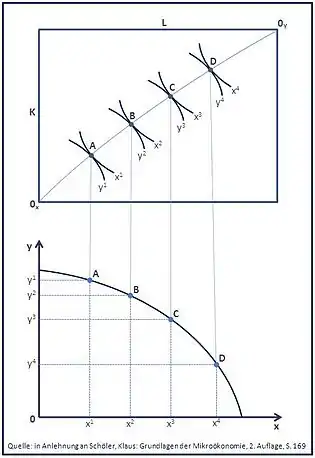
Abb. 5: Herleitung der Transformationskurve aus der Edgeworth-Box

Um die Herleitung verständlicher zu machen, bedient man sich dem im oberen Teil der Abb. 5 zu erkennenden Schachteldiagramm, auch genannt Edgeworth-Box. Dabei wird von der Produktion zweier Güter und nur begrenzt zur Verfügung stehenden Produktionsfaktoren ausgegangen. Unter dieser Bedingung werden die Isoquanten für die beiden darzustellenden Güter X und Y in das Diagramm abgetragen. Verbindet man nun die Tangentialpunkte, also die Berührungspunkte der Isoquanten (in der Grafik A, B, C und D), erhält man die Linie der effizienten Produktion, auch als Kontraktkurve bezeichnet. Die Lage der sich berührenden Isoquanten zum jeweiligen Ursprung repräsentiert die verschiedenen Produktionsmengen in diesen Punkten. Die Steigung der Isoquanten wird bestimmt durch das Verhältnis der Grenzproduktivitäten. Da in den Berührungspunkten die Steigung der jeweiligen Isoquanten (hier der Güter X und Y) identisch ist, muss demnach auch das Verhältnis der Grenzproduktivitäten der beiden Güter einen gleichen Wert annehmen. Somit kann von Gut X nicht mehr hergestellt werden, ohne auf eine bestimmte Menge des Gut Y zu verzichten – die Tangentialpunkte stellen folglich durch die Isoquanten bestimmte Pareto-optimale Mengenkombinationen der Güter X und Y dar. Diese in der Edgeworth-Box abgebildeten Gütermengenkombinationen A, B, C und D lassen sich in ein bekanntes X-Y-Produktmengendiagramm übertragen.[18][19] In der Abb. 5 erfolgt diese Übertragung senkrecht nach unten, man beachte an dieser Stelle, dass die Übertragungslinien dabei nicht völlig senkrecht verlaufen müssen, da die Achsen beider Diagramme durch verschiedene Variablen bezeichnet sind. Verbindet man nun wiederum die übertragenen Punkte A, B, C und D im unteren Diagramm, entsteht die Produktionsmöglichkeitenkurve.[20] Diese verläuft in der Abbildung exemplarisch konkav, denkbar sind auch andere Verläufe (siehe Lage und Gestalt der Kurve).

Mathematische Herleitung

Mathematisch lässt sich die Transformationsfunktion aus den Produktionsfunktionen der beiden Güter X und Y herleiten. Dies soll anhand einer Beispiel-Rechnung unter gewissen Annahmen gezeigt werden. Hierbei wird davon ausgegangen, dass es sich um zwei linear homogene Produktionsfunktionen mit gleichen partiellen Produktionselastizitäten von ½ handelt.[21] Weiterhin gibt es analog zur grafischen Herleitung nur zwei Produktionsfaktoren, Kapital und Arbeit. Die Produktionsfunktionen für die Güter X und Y lauten:

(1)

X=K_{x}^{1/2}L_{x}^{1/2}

,

(2)

Y=2K_{y}^{1/2}L_{y}^{1/2}

.

$X$ : Gut X
$Y$ : Gut Y
$K$ : Produktionsfaktor Kapital
$L$ : Produktionsfaktor Arbeit

Wie bereits erläutert, sind die Gütermengenkombinationen Pareto-optimal, die Steigung der Isoquanten – somit die Grenzraten der technischen Substitution – der Güter X und Y müssen in den Tangentialpunkten identisch sein.[22] Daher ergibt sich:

(3)

{GRTS}_{X}={\frac {{GP}_{L,X}}{{GP}_{K,X}}}={\frac {{dX/dL}_{X}}{{dX/dK}_{X}}}={\frac {{(1/2)X/L}_{X}}{{(1/2)X/K}_{X}}}={\frac {K_{X}}{L_{X}}}

,

(4)

{GRTS}_{Y}={\frac {{GP}_{L,Y}}{{GP}_{K,Y}}}={\frac {{dY/dL}_{Y}}{{dY/dK}_{Y}}}={\frac {{(1/2)Y/L}_{Y}}{{(1/2)Y/K}_{Y}}}={\frac {K_{Y}}{L_{Y}}}

.

$GRTS$ : Grenzrate der technischen Substitution
$GP$ : Grenzproduktivität
$d$ : Differential

Werden die Beziehungen (3) und (4) gleichgesetzt, erhält man das gewünschte Optimum für das vorliegende Beispiel:

{\frac {K_{X}}{L_{X}}}={\frac {K_{Y}}{L_{Y}}}

.

Anschließend wird für:

\operatorname {\mathit {K_{Y}}} ={K_{g}}-{K_{X}}

und

\operatorname {\mathit {L_{Y}}} ={L_{g}}-{L_{X}}

sowie

\operatorname {\mathit {K_{X}}} ={K_{g}}-{K_{Y}}

und

\operatorname {\mathit {L_{X}}} ={L_{g}}-{L_{Y}}

$K_{g}$ : Produktionsfaktor Kapital gesamt
$L_{g}$ : Produktionsfaktor Arbeit gesamt

eingesetzt und umgeformt, man erhält somit:

(5)

K_{X}={\frac {K_{g}}{L_{g}}}L_{X}

,

(6)

K_{Y}={\frac {K_{g}}{L_{g}}}L_{Y}

.

Die Gleichungen (5) und (6) zeigen deutlich eine lineare Beziehung der einzusetzenden Faktoren auf. Aus Vereinfachungsgründen wurden in dem zu Grunde liegenden Beispiel lineare Produktionsfunktionen verwendet. So ergibt sich auch für die in Abb. 5 in der Edgeworth-Box zu erkennende Kontraktkurve – für die Verbindungslinie der Tangentialpunkte A bis D – ein linearer Verlauf mit dem Verhältnis $\operatorname {\mathit {K_{g}}} /{L_{g}}$ als Steigung. Im folgenden Schritt zur Herleitung der Transformationsfunktion wird der Ausdruck der effizienten Kapitalverwendung (5) in die Produktionsfunktion von Gut X (1) gesetzt:

(7)

X=\left({\frac {K_{g}}{L_{g}}}L_{X}\right)^{1/2}L_{x}^{1/2}=\left({\frac {K_{g}}{L_{g}}}\right)^{1/2}L_{x}

.

Über die Funktion (7) umgestellt nach $\operatorname {\mathit {L_{X}}}$ gelangt man zur Arbeitsnachfrage von:

(8)

L_{X}=\left({\frac {L_{g}}{K_{g}}}\right)^{1/2}X

.

Setzt man die in die Produktionsfunktion von Gut Y (2) für $\operatorname {\mathit {K_{Y}}}$ den Ausdruck der Funktion (6) ein und ersetzt wiederum $\operatorname {\mathit {L_{Y}}}$ durch $\operatorname {\mathit {L_{Y}}} ={Lg}-{L_{X}}$ , erhält man den nachstehenden Funktionsausdruck:

Y=2\left({\frac {K_{g}}{L_{g}}}\right)^{1/2}\left({L_{g}}-{L_{X}}\right)

und nach dem Einsetzen der Arbeitsnachfrage (8) für $\operatorname {\mathit {L_{X}}}$ sowie einigen Umformungen letztendlich:

(9)

Y=2\left({K_{g}}{L_{g}}\right)^{1/2}-2X

.

Bezogen auf die vorangestellten Produktionsfunktionen (1) und (2) stellt die Gleichung (9) die dazugehörige Transformationsfunktion dar.[23] Oben stehende mathematische Herleitung ist dabei nur als exemplarisch für die beiden fiktiv angenommenen Produktionsfunktionen und damit für eine spezielle lineare Produktionsmöglichkeitenkurve zu betrachten. Analog der oben angeführten Vorgehensweise – jedoch mathematisch anspruchsvoller – können sowohl eine konkave Transformationskurve wie in Abb. 5 gezeigt, als auch sämtliche individuell verlaufende Kapazitätslinien analytisch hergeleitet werden.

Anwendung, Beispiel

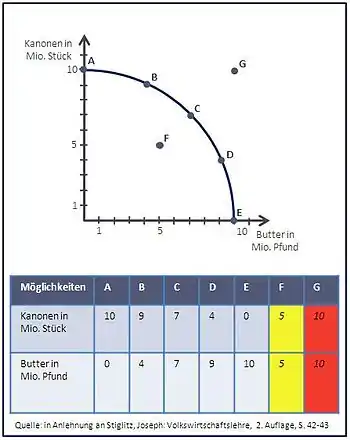
Abb. 6: Modell-Volkswirtschaft im Zwei-Güter-Fall

Abschließend sollen mittels eines in der volkswirtschaftlichen Literatur oft verwendeten Standardbeispiels die verschiedenen Aspekte der Produktionsmöglichkeitenkurve noch einmal verständlicher erläutert werden. Im genannten Beispiel wird von einer Modell-Volkswirtschaft ausgegangen, die lediglich zwei Güter – Kanonen und Butter – produzieren kann.[24] Die Erzeugnisse stehen dabei stellvertretend für die Kategorien Konsumgüter und Verteidigungsgüter.[25] Abb. 6 zeigt verschiedene Produktionsmöglichkeiten der betrachteten Volkswirtschaft, so wird die Produktion dahingehend eingeschränkt, dass entweder nur 10 Mio. Stück Kanonen oder 10 Mio. Pfund Butter hergestellt werden können. Dies verdeutlicht die in der Realität bestehende Knappheit von Inputfaktoren. Es muss also eine Entscheidung getroffen werden, ob man einen der Extremfälle – nur Konsumgüter (Butter) bzw. nur Verteidigungsgüter (Kanonen) – wählt, oder etwa eine der zahlreichen effizienten Gütermengenkombinationen auf der Transformationskurve (Pkt. B–D). Darüber hinaus besteht die Möglichkeit, alle ineffizienten Kombinationen unterhalb der Kurve (beispielsweise Pkt. F) zu produzieren.[26] In der vorangegangenen Betrachtung wurde bereits festgestellt, dass eine Entscheidung treffen ferner bedeutet, einen Verzicht im Sinne von Opportunitätskosten in Kauf zu nehmen. Es sei angenommen, in der Ausgangssituation befindet man sich im Anwendungsbeispiel in Punkt B, d. h., es werden 9 Mio. Kanonen und 4 Mio. Pfund Butter produziert. Aufgrund zunehmender Bevölkerungszahlen stellt sich nun ein höherer Bedarf an Lebensmitteln ein – es wird daher entschieden 3 Mio. Pfund mehr Butter herzustellen. Zieht man die Grafik in Abb. 6 zu Hilfe, ist zu erkennen, dass sich Punkt B bereits auf der Kurve befindet, somit alle zur Verfügung stehenden Ressourcen genutzt sind. Um 3. Mio. Pfund mehr von der Butter produzieren zu können, bleibt also nur die Gütermengenkombination in Punkt C, das bedeutet einen Verzicht in Höhe von 2 Mio. Stück Kanonen – dieser Verzicht an Kanonen wird als Opportunitätskosten betrachtet.

Findet eine Bewegung auf der Kurve statt, werden also Mengen des einen Produkts (Kanonen) in Mengen des anderen Produkts (Butter) transformiert. Da die Produktionsmöglichkeitenkurve in Abb. 6 nach außen gekrümmt ist, verändert sich das Transformationsverhältnis von Kanonen in Butter entlang der Funktion. Das Beispiel zeigt damit deutlich das Gesetz des abnehmenden Ertragszuwachses.[27] Während bei einem Wechsel von der Mengenkombination A zu B für einen Verzicht von 1 Mio. Stück Kanonen gleich 4 Mio. Pfund Butter substituiert werden können, bleibt bei einer Veränderung von Punkt D zu E für einen Verzicht von 4 Mio. Stück Kanonen gerade einmal ein Ertrag von 1 Mio. Pfund Butter. Analog der abnehmenden Erträge ändern sich die Alternativkosten.

Sollte das volkswirtschaftliche Ziel sein, die gesamtwirtschaftliche Produktion zu erhöhen, beispielsweise zur Gütermengenkombination im Punkt G zu gelangen, ist dies unter gleichbleibenden Bedingungen nicht realisierbar. In diesem Fall wäre es notwendig, den Input bzw. die Faktorausstattung zu erhöhen. Eine Ausweitung der Produktionskapazitäten durch eine Erhöhung der Produktionsfaktoren Arbeit, Kapital oder Wissen, speziell durch Zuwanderung von Gastarbeitern, Kapitalzufluss aus dem Ausland oder neue technische Forschungserkenntnisse, kann dieses Problem lösen.[28]

Literatur

Ulrich Brösse: Einführung in die Volkswirtschaftslehre – Mikroökonomie. Oldenbourg, München/Wien 1997, ISBN 3-486-23699-7.
Horst Demmler: Einführung in die Volkswirtschaftslehre. 7. Auflage. Oldenbourg, München/Wien 2001, ISBN 3-486-25623-8.
Gustav Dieckheuer: Internationale Wirtschaftsbeziehung. 5. Auflage. Oldenbourg, München/Wien 2001, ISBN 3-486-25806-0.
Ulrich Fehl, Peter Oberender: Grundlagen der Mikroökonomie. 9. Auflage. München 2004, ISBN 3-8006-3107-5.
Rainer Fischbach: Volkswirtschaftslehre – Einführung und Grundlagen. 8. Auflage. Oldenbourg, München 1994, ISBN 3-486-22792-0.
Gabriele Hildmann: Mikroökonomie – Intensivtraining. In: Volker Drosse, Ulrich Vossebein (Hrsg.): Repetitorium Wirtschaftswissenschaften. 2. Auflage. München 2005, ISBN 3-409-22620-6.
Gerhard Kolb: Grundlagen der Volkswirtschaftslehre. München 1991, ISBN 3-8006-1568-1.
Paul R. Krugman, Maurice Obstfeld: – Theorie und Politik der Außenwirtschaft. 7. Auflage. München 2006, ISBN 3-8273-7199-6.
Robert S. Pindyck, Daniel L. Rubinfeld: Mikroökonomie. 5. Auflage. München 2003, ISBN 3-8273-7025-6.
Paul A. Samuelson, William D. Nordhaus: Volkswirtschaftslehre – Grundlagen der Makro- und Mikroökonomie. 8. Auflage. Köln 1987, ISBN 3-7663-0986-2.
Klaus Schöler: Grundlagen der Mikroökonomie. 2. Auflage. München 2004, ISBN 3-8006-3065-6.
Joseph E. Stiglitz: Volkswirtschaftslehre. 2. Auflage. München/Wien 1999 3-486-23379-3
Alfred Stobbe: Mikroökonomie. 2. Auflage. Berlin / Heidelberg / New York 1991, ISBN 3-540-54136-5.
Artur Woll: Allgemeine Volkswirtschaftslehre. 14. Auflage. München 2003, ISBN 3-8006-2973-9.
Hal R. Varian: Grundzüge der Mikroökonomie. 6. Auflage. München/Wien 2004, ISBN 3-486-27453-8.
Andreas Zenthöfer: Grundlagen der Mikroökonomie. In: H.P. Richter (Hrsg.): Wirtschaftswissenschaftliche Grundkurse. Kiel 2006, ISBN 3-935150-51-2.

Weblinks

Transformationskurve – Definition im Gabler Wirtschaftslexikon
Transformationskurve – W. Lorenz: mikrooekonomie.de – vollständiger Einsteiger-Artikel
- Auf, über und unter der Transformationskurve – Vertiefung des Einsteigerartikels
- Transformationskurve und Opportunitätskosten – Vertiefung des Einsteigerartikels

Einzelnachweise

Hal R. Varian: Grundzüge der Mikroökonomie. 2004, S. 590.
Gerhard Kolb: Grundlagen der Volkswirtschaftslehre. 1991, S. 42–43.
Artur Woll: Allgemeine Volkswirtschaftslehre. 2003, S. 60.
Paul R. Krugman, Maurice Obstfeld: Internationale Wirtschaft – Theorie und Politik der Außenwirtschaft. 2006, S. 59.
Robert S. Pindyck, Daniel L. Rubinfeld: Mikroökonomie. 2003, S. 814.
Robert S. Pindyck, Daniel L. Rubinfeld: Mikroökonomie. 2003, S. 821.
Artur Woll: Allgemeine Volkswirtschaftslehre. 2003, S. 59.
Paul A. Samuelson, William D. Nordhaus: Volkswirtschaftslehre – Grundlagen der Makro- und Mikroökonomie. 1987, S. 66–67.
Ulrich Fehl, Peter Oberender: Grundlagen der Mikroökonomie. 2004, S. 265–269.
Andreas Zenthöfer: Grundlagen der Mikroökonomie. 2006, S. 55–56.
Gabriele Hildmann: Mikroökonomie – Intensivtraining. 2005, S. 92–95.
Ulrich Fehl, Peter Oberender: Grundlagen der Mikroökonomie. 2004, S. 267.
Ulrich Brösse: Einführung in die Volkswirtschaftslehre – Mikroökonomie. 1997, S. 61.
Alfred Stobbe: Mikroökonomie. 1991, S. 195.
Paul A. Samuelson, William D. Nordhaus: Volkswirtschaftslehre – Grundlagen der Makro- und Mikroökonomie. 1987, S. 75–80.
Gerhard Kolb: Grundlagen der Volkswirtschaftslehre. 1991, S. 43.
Alfred Stobbe: Mikroökonomie. 1991, S. 197.
Klaus Schöler: Grundlagen der Mikroökonomie. 2004, S. 168.
Gabriele Hildmann: Mikroökonomie – Intensivtraining. 2005, S. 93–94.
Klaus Schöler: Grundlagen der Mikroökonomie. 2004, S. 168–169.
Klaus Schöler: Grundlagen der Mikroökonomie. 2004, S. 169–170.
Robert S. Pindyck, Daniel L. Rubinfeld: Mikroökonomie. 2003, S. 282–283.
Klaus Schöler: Grundlagen der Mikroökonomie. 2004, S. 169–171.
Joseph E. Stiglitz: Volkswirtschaftslehre. 1999, S. 42.
Ulrich Brösse: Einführung in die Volkswirtschaftslehre – Mikroökonomie. 1997, S. 59.
Paul A. Samuelson, William D. Nordhaus: Volkswirtschaftslehre – Grundlagen der Makro- und Mikroökonomie. 1987, S. 65.
Joseph E. Stiglitz: Volkswirtschaftslehre. 1999, S. 44.
Ulrich Brösse: Einführung in die Volkswirtschaftslehre – Mikroökonomie. 1997, S. 60–61.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Varian.590-1] Hal R. Varian: Grundzüge der Mikroökonomie. 2004, S. 590.

[Kolb-2] Gerhard Kolb: Grundlagen der Volkswirtschaftslehre. 1991, S. 42–43.

[Woll-3] Artur Woll: Allgemeine Volkswirtschaftslehre. 2003, S. 60.

[Krugman-4] Paul R. Krugman, Maurice Obstfeld: Internationale Wirtschaft – Theorie und Politik der Außenwirtschaft. 2006, S. 59.

[Pindyck.814-5] Robert S. Pindyck, Daniel L. Rubinfeld: Mikroökonomie. 2003, S. 814.

[Pindyck.821-6] Robert S. Pindyck, Daniel L. Rubinfeld: Mikroökonomie. 2003, S. 821.

[Woll.59-7] Artur Woll: Allgemeine Volkswirtschaftslehre. 2003, S. 59.

[Samuelson-8] Paul A. Samuelson, William D. Nordhaus: Volkswirtschaftslehre – Grundlagen der Makro- und Mikroökonomie. 1987, S. 66–67.

[Fehl-9] Ulrich Fehl, Peter Oberender: Grundlagen der Mikroökonomie. 2004, S. 265–269.

[Zenthöfer-10] Andreas Zenthöfer: Grundlagen der Mikroökonomie. 2006, S. 55–56.

[Hildmann.92-95-11] Gabriele Hildmann: Mikroökonomie – Intensivtraining. 2005, S. 92–95.

[Fehl_1-12] Ulrich Fehl, Peter Oberender: Grundlagen der Mikroökonomie. 2004, S. 267.

[Brösse.61-13] Ulrich Brösse: Einführung in die Volkswirtschaftslehre – Mikroökonomie. 1997, S. 61.

[Stobbe-14] Alfred Stobbe: Mikroökonomie. 1991, S. 195.

[Samuelson_1-15] Paul A. Samuelson, William D. Nordhaus: Volkswirtschaftslehre – Grundlagen der Makro- und Mikroökonomie. 1987, S. 75–80.

[Kolb_1-16] Gerhard Kolb: Grundlagen der Volkswirtschaftslehre. 1991, S. 43.

[Stobbe_1-17] Alfred Stobbe: Mikroökonomie. 1991, S. 197.

[Schöler.168-18] Klaus Schöler: Grundlagen der Mikroökonomie. 2004, S. 168.

[Hildmann.93-94-19] Gabriele Hildmann: Mikroökonomie – Intensivtraining. 2005, S. 93–94.

[Schöler.168-169-20] Klaus Schöler: Grundlagen der Mikroökonomie. 2004, S. 168–169.

[Schöler.169-170-21] Klaus Schöler: Grundlagen der Mikroökonomie. 2004, S. 169–170.

[Pindyck.282-283-22] Robert S. Pindyck, Daniel L. Rubinfeld: Mikroökonomie. 2003, S. 282–283.

[Schöler.169-171-23] Klaus Schöler: Grundlagen der Mikroökonomie. 2004, S. 169–171.

[Stiglitz-24] Joseph E. Stiglitz: Volkswirtschaftslehre. 1999, S. 42.

[Brösse.59-25] Ulrich Brösse: Einführung in die Volkswirtschaftslehre – Mikroökonomie. 1997, S. 59.

[Samuelson_2-26] Paul A. Samuelson, William D. Nordhaus: Volkswirtschaftslehre – Grundlagen der Makro- und Mikroökonomie. 1987, S. 65.

[Stiglitz.44-27] Joseph E. Stiglitz: Volkswirtschaftslehre. 1999, S. 44.

[Brösse.60-61-28] Ulrich Brösse: Einführung in die Volkswirtschaftslehre – Mikroökonomie. 1997, S. 60–61.