Kontraktkurve
Die Kontraktkurve ist ein Begriff der Volkswirtschaftslehre und bezeichnet die Kurve in einer Edgeworth-Box, die alle Pareto-optimalen Lösungen für den beidseitig vorteilhaften Tausch zweier Gütermengen zwischen zwei Haushalten verbindet, unter der Gegebenheit der Anfangsausstattungen der Haushalte. In der Produktionstheorie sind es, im Gegensatz zur Haushaltstheorie, zwei Unternehmen, die zwei Inputfaktormengen zwischen sich tauschen.
Die Wirtschaftssubjekte A und B versuchen, ihre Anfangsausstattung mit den Gütern X und Y dergestalt zu verändern, dass ihr Nutzen maximiert wird. Beide tauschen so lange, bis ein Marktgleichgewicht erreicht wird. Ein Pareto-optimales Marktgleichgewicht liegt dann vor, wenn keiner seinen Nutzen erhöhen kann, ohne den des anderen zu senken.
Geometrisch ist die Kurve die Verbindung aller Punkte, in denen sich die Indifferenzkurven der beiden Wirtschaftssubjekte tangieren (sie also identische Grenzraten der Substitution aufweisen).
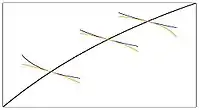
Die schwarze Linie stellt die Kontraktkurve dar, die blauen Kurven sind beispielhafte Indifferenzkurven von Wirtschaftssubjekt A, die orangen Kurven die dazugehörigen Indifferenzkurven von B.
Theoretisch können die Wirtschaftssubjekte alle Punkte auf der Kontraktkurve durch Tausch erhalten. Sobald ein Punkt auf der Kurve erreicht wird, tritt keine Veränderung mehr ein, da sich eines der beiden Individuen durch Tausch auf jeden Fall schlechter stellen würde. Welcher Punkt tatsächlich erreicht wird, hängt davon ab, welche Anfangsausstattungen die Individuen von beiden Gütern haben und welche Nutzenfunktionen sie besitzen. Die Kontraktkurve muss nicht notwendigerweise durch die beiden Ecken der Edgeworth-Box verlaufen.
Punkte auf der Kontraktkurve erfüllen sowohl das erste Wohlfahrtstheorem als auch das zweite Wohlfahrtstheorem.
Wichtig ist die Anmerkung, dass die Kontraktkurve lediglich optimale Verteilungen unter dem Gesichtspunkt der Effizienz hervorhebt. Nicht berücksichtigt werden Probleme der Verteilungsgerechtigkeit. Diese Einschränkung ist insbesondere von Bedeutung, wenn ein Modellergebnis auf reale Situationen übertragen werden soll – ein nicht effizienter Punkt kann durchaus von allen Teilnehmern bevorzugt werden, weil andere Aspekte eine Rolle spielen.
Beispiel
Auf einer einsamen Insel leben Robinson und Freitag von der übrigen Welt abgeschnitten. Robinson hat eine Anfangsausstattung von 40 Kokosnüssen und 10 Fischen, während Freitag mit 10 Kokosnüssen und 40 Fischen ausgestattet ist. Weitere Güter sind nicht von Belang.
Beide Insulaner haben eine Nutzenfunktion von , wobei die Anzahl konsumierter Kokosnüsse und die Anzahl konsumierter Fische darstellt. Diese führt dazu, dass beide den Besitz von Kokosnüssen und Fischen in identischer Anzahl anstreben. Offensichtlich erfüllt die Anfangsausstattung diesen Wunsch nicht. Wird Handel zugelassen, werden beide versuchen, ihre Güterbündel zu verbessern.
Befiehlt dagegen ein wohlmeinender Diktator eine Umverteilung, die beispielsweise folgende Bündel ergibt
- Robinson: 30 Fische, 30 Kokosnüsse sowie Freitag: 20 Fische, 20 Kokosnüsse
- Robinson: 25 Fische, 25 Kokosnüsse sowie Freitag: 25 Fische, 25 Kokosnüsse
- Robinson: 20 Fische, 20 Kokosnüsse sowie Freitag: 30 Fische, 30 Kokosnüsse
so wird kein weiterer Handel angestrebt werden. Beide haben ein (gemäß ihren Möglichkeiten) optimales Nutzenbündel erhalten und können sich nicht weiter verbessern, ohne Fische oder Kokosnüsse vom anderen zu stehlen und dessen Nutzen so zu vermindern.
Daher sind keine Pareto-Verbesserungen mehr möglich, die angegebenen Verteilungen sind Pareto-optimal.
Die Kontraktkurve stellt die Menge aller Pareto-optimalen Verteilungen dar, gemäß derer jeder Teilnehmer mindestens genauso gut gestellt wird, wie gemäß der Anfangsausstattung. In diesem Fall handelt es sich also um alle Verteilungen, bei denen sowohl Robinson als auch Freitag eine jeweils identische Anzahl von Kokosnüssen und Fischen besitzen und jeder mindestens 20 Kokosnüsse und Fische besitzt.
In der Edgeworth-Box (vgl. Zeichnung oben) würde die Kontraktkurve in diesem Beispiel die Gestalt einer geraden Linie vom Punkt (20,20) (Robinson hat 20 Fische und Kokosnüsse, Freitag hat 30 Fische und Kokosnüsse) zum Punkt (30,30) (Robinson hat 30 Fische und Kokosnüsse, Freitag 20 Fische und Kokosnüsse) annehmen. Die drei genannten Beispielverteilungen liegen dann auf dieser Linie.
Literatur
- Hal Varian: Intermediate Microeconomics. Kapitel 30 (S. 540 ff.), 6th Edition, W. W. Norton & Company, New York/London 2003, ISBN 0-393-97830-3.
- Microeconomics Kapitel 16 (S. 563 ff.), Pindyck, Robert S., Rubinfeld Daniel L., 6th Edition, Prentice-Hall Series in Economics, 2004, ISBN 0-130-08461-1.