Sudoku

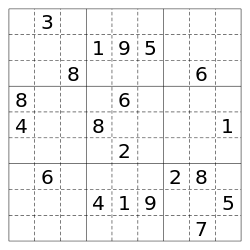
Sudoku (japanisch 数独 Sūdoku, kurz für 数字は独身に限る Sūji wa dokushin ni kagiru, wörtlich so viel wie „Ziffern dürfen nur einmal vorkommen“) ist eine Gattung von Logikrätseln, die aus den lateinischen Quadraten entstand. In der üblichen Version ist es das Ziel, ein 9×9-Gitter mit den Ziffern 1 bis 9 so zu füllen, dass jede Ziffer in jeder Einheit (Spalte, Zeile, Block = 3×3-Unterquadrat) genau einmal vorkommt – und in jedem der 81 Felder exakt eine Ziffer vorkommt. Ausgangspunkt ist ein Gitter, in dem bereits mehrere Ziffern vorgegeben sind. In Zeitungen und Zeitschriften werden heute regelmäßig Sudokurätsel veröffentlicht.

Die moderne Form des Sudoku wurde von Howard Garns erfunden. Erstmals im Jahr 1979 unter dem Namen Number Place in einer Rätselzeitschrift in den Vereinigten Staaten veröffentlicht, wurde es erst ab 1984 zunächst in Japan populär, wo es auch seinen heutigen Namen Sudoku erhielt.

Sudoku-Rätsel mit 20 Vorgaben …

… mit allen verbliebenen Kandidaten …

… und seiner (eindeutigen) Lösung

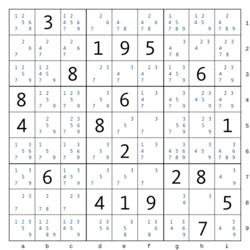
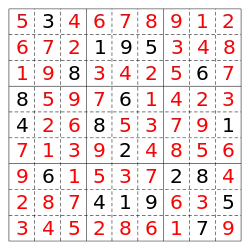
Ursprung

Die frühesten Vorläufer des Sudoku waren die lateinischen Quadrate des Schweizer Mathematikers Leonhard Euler (1707–1783). Anders als Sudokus waren diese jedoch nicht in Blöcke (Unterquadrate) unterteilt. Dieser Annahme widerspricht jedoch die im 8. Jahrhundert durch Abu Abdullah Dschabir ibn Hayyan el-Sufi verschriftlichte islamische Version, den sogenannten „Buduh“.[1]

Von 1892 bis zum Ausbruch des Ersten Weltkrieges publizierten die französischen Zeitungen Le Siècle und La France regelmäßig Rätselquadrate unter dem Titel „Carré magique diabolique“. Diese frühen Publikationen setzten sich auf Dauer nicht durch. Ihnen fehlte ebenfalls die Unterteilung in Unterblöcke.

Das heutige Sudoku mit Einbeziehung der Blöcke (neben Zeilen und Spalten) wurde erstmals im Jahr 1979 anonym von dem damals 74-jährigen Architekten und freischaffenden „Rätselonkel“ Howard Garns[2] in der Zeitschrift Dell Pencil Puzzles & Word Games (engl. Bleistifträtsel & Wortspiele) als „Number Place“ (engl. Zahlenplatz) veröffentlicht.[3][4]

Die ersten Sudokus wurden zwar in den Vereinigten Staaten publiziert, seinen Durchbruch erlebte das Zahlenrätsel jedoch erst zwischen 1984 und 1986, als die japanische Zeitschrift Nikoli es zunächst unter dem Namen „Sūji wa dokushin ni kagiru“ (deutsch etwa: „Isolieren Sie die Zahlen; die Zahlen dürfen nur einmal vorkommen“) regelmäßig abdruckte. Im Jahr 1986 wurde diese sperrige Bezeichnung vom Herausgeber Maki Kaji unter Beibehaltung der jeweils ersten Kanji-Zeichen zu „Sudoku“ (数独, sūdoku) verkürzt und als Marke registriert,[5] deshalb werden selbst heute noch diese Rätsel in manchen japanischen Zeitschriften unter dem englischen Begriff „Number Place“ oder seiner Entsprechung in Katakana (ナンバープレース, Nambā Purēsu) abgedruckt; auch die Abkürzung „Nanpure/Nampure“ (ナンプレ, unter anderem als Spiel für Sonys PlayStation) ist teilweise üblich.[3]

Der Neuseeländer Wayne Gould lernte Sudoku auf einer Japanreise kennen und entwickelte innerhalb von sechs Jahren eine Software, die neue Sudokus per Knopfdruck erzeugen konnte. Anschließend bot er seine Rätsel der Times in London an. Die Tageszeitung druckte die ersten Sudoku-Rätsel im November 2004 ab und trug dadurch zur Verbreitung der Rätsel bei.[6]

In Deutschland, Österreich und der Schweiz führte der regelmäßige Abdruck in Tageszeitungen und Fernsehzeitschriften seit Ende 2005 zu einer raschen Verbreitung. Das Prinzip des Rätsels unterliegt nicht dem Urheberrecht. Somit sind keine Gebühren an einen Lizenzgeber zu entrichten. Sudokus können jederzeit frei erstellt und veröffentlicht werden.

Seit Ende 2005 sind tragbare elektronische Sudoku-Geräte erhältlich. Des Weiteren gibt es Sudoku als einfaches Brettspiel und interaktiv online (Internet) sowie offline als Computerspiel. Das erste Computerspiel wurde bereits im Jahr 1989 von Softdisk unter dem Label Loadstar/Softdisk Publishing, Inc. für den C64 mit dem Namen Digithunt herausgebracht.

Varianten

Im Folgenden werden Varianten für Sudokus mit ergänzten oder modifizierten Regeln beschrieben. Die Varianten können auch miteinander kombiniert werden.

Killer-Sudoku

Eine Variante des Sudoku ist das Killer-Sudoku. Die meist 81 Felder sind in kleine Bereiche gruppiert, welche jeweils mit einer kleinen Zahl versehen sind. Diese gibt die Summe aller Zahlen in diesem Bereich an. Killer-Sudoku trainiert neben dem logischen Denkvermögen somit auch das Kopfrechnen.

X-Sudoku

X-Sudoku (Musterbeispiel)

X-Sudoku (auch Diagonal- oder Magisches Sudoku) ist eine Variante, bei der (zusätzlich zu den Bedingungen des normalen Sudokus) auf jeder der beiden Hauptdiagonalen, die gemeinsam ein „X“ ergeben, jede Zahl nur einmal vorkommen darf. Sudoku- und andere Rätsel-Zeitschriften veröffentlichen regelmäßig X-Sudokus in verschiedenen Größen. Neben der Standardgröße 9×9 kommen auch andere Größen vor, etwa 8×8 (mit 2×4-Blöcken). Bei letzterem verfügen die beiden Diagonalen über kein gemeinsames Schnittfeld. Für X-Sudokus in der Standardgröße 9×9 ist die Bestimmung der Mindestanzahl vorbelegter Felder nicht gelöst. Man kennt eindeutig lösbare X-Sudokus mit 12 Vorbelegungen, doch es ist nicht bekannt, ob es auch welche mit 11 Vorbelegungen gibt.[7]

Hyper-Sudoku

Eine weitere Variante ist das Hyper-Sudoku (auch „Fenstersudoku“). Ähnlich wie das X-Sudoku unterscheidet sich auch dieses vom normalen Sudoku durch zusätzliche Einheiten, in denen jede Zahl genau einmal vorkommen darf. Ein Hyper-Sudoku hat vier zusätzliche Blöcke, die mit einem Feld Abstand zum Rand und zueinander über den neun Blöcken des normalen Sudokus liegen. Dadurch ändert sich der Lösungsansatz etwas, da man verstärkt auf die Blöcke und weniger auf die Zeilen und Spalten achten muss.

Fudschijama

Inzwischen gibt es auch Sudokus – meist als Fudschijama bezeichnet – mit 4×4 Blöcken und somit 256 (= 16×16) Feldern, in die je 16 verschiedene Zahlen, Buchstaben oder Symbole verteilt werden sowie „erweiterte Sudokus“ mit 4×3 Blöcken und 144 (also jeweils 12×12) Feldern und „Mini-Sudokus“ für Einsteiger mit 2×3 Blöcken und 36 (also 6×6) Feldern. Auch andere Blockgrößen, wie z. B. 5×5 (625 Felder) oder gar 6×6 (1296 Felder) sind denkbar, die gelegentlich auch Jumbo-Sudoku heißen. Für Kinder gibt es 4×4-Sudokus (auch Mini-Sudoku genannt) mit einer Zweier-Kantenlänge pro Block, dabei werden also nur 4 Ziffern oder Bildsymbole eingetragen.

Allgemein kann ein Sudoku aus a×b Blöcken bestehen, die jeweils b×a Felder enthalten. Das Sudoku enthält insgesamt (a×b)×(a×b) Felder, in die a×b verschiedene Symbole einzutragen sind.

Multi-Sudoku

Ein Multi-Sudoku besteht aus mehreren Sudokus, die sich in Teilbereichen überlappen. Charakteristisch hierfür ist, dass die dazugehörigen Sudokus jeweils für sich allein genommen nicht eindeutig lösbar sind, sondern erst die Kombination die Lösung eindeutig macht.

Samurai Sudoku (Musterbeispiel)

Ein Beispiel hierfür ist das „Samurai Sudoku“ oder „Gattai 5“, das Anfang 2006 aufkam. Fünf Standard-Sudokus sind teilweise überlappend X-förmig angeordnet – eines zentral und an jeder Ecke ein weiteres. Dabei teilt sich jedes dieser vier Eck-Sudokus genau einen der vier äußeren Eckblöcke des Zentral-Sudokus, dadurch ergeben sich insgesamt 369 Felder verteilt auf 41 Blöcke. Weitere Variationen setzen acht (Gattai 8), dreizehn (Gattai 13) oder mehr Sudokus zusammen. Diese Varianten werden als Monster-Samurai bezeichnet.

Nonomino-Sudoku

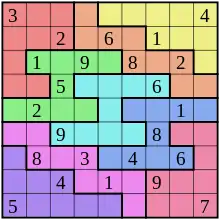
Ein Nonomino-Sudoku, erschienen im Sunday Telegraph

Bei dieser Variante (auch bekannt als „Freiform-Sudoku“ oder „Chaos-Sudoku“) sind die Blöcke des Sudokus unregelmäßig geformt, bestehen aber nach wie vor aus neun Feldern (englisch Jigsaw Sudoku oder Nonomino Sudoku), sogenannten Nonominos. Ein Beispiel hierfür sind Sudokus mit treppenförmiger Begrenzung der Blöcke (englisch Stairstep Sudoku).

Als Erweiterung dieser Variante kann man „Torus-Sudoku“ verstehen. Hierbei setzen sich die unregelmäßigen Blöcke über den Rand des Sudokus hinaus auf die gegenüberliegende Seite fort. Der Name rührt daher, dass die Blöcke zusammenhängend werden, wenn man das Quadrat aufrollt und zu einem Torus zusammenklebt.

Roxdoku

Eine weitere Variante ist dreidimensional und besteht in der Grundform aus 3×3×3 Würfeln als Felder. Hier darf nicht nur in Zeilen und Spalten, sondern auch in den Ebenen keine Zahl beziehungsweise Buchstabe doppelt sein. Außerdem ist es auch hier möglich, so wie in der 2D-Version mit 4×4×4 Würfeln oder gar noch mehr zu spielen. Roxdokus werden als Computerspiel angeboten, da hier die Möglichkeit besteht, das gesamte „Spielfeld“ in alle Richtungen zu drehen.

Even-Odd-Sudoku

Bei einem Even-Odd-Sudoku ist für einzelne Felder vorgegeben, dass in diese nur gerade (englisch even) oder nur ungerade (englisch odd) Zahlen eingetragen werden dürfen.

Vergleichssudoku

Comparison Sudoku (Musterbeispiel)

Ein Vergleichssudoku (englisch Comparison Sudoku) erschien in Österreich erstmals am 2. August 2006 in der Tageszeitung Der Standard unter LeichtSinn. In einem Vergleichssudoku werden keine Zahlen vorgegeben. Stattdessen sind die Grenzlinien aller Einzelfelder eines jeden Blocks mit einer Ein- beziehungsweise Ausbuchtung zu jedem Nachbarfeld versehen – im Sinne von < (kleiner als) oder > (größer als). Alle üblichen Sudokuregeln gelten auch hier, nur müssen bei dieser Variante alle Zahlen zusätzlich der Kleiner- beziehungsweise Größerregel folgen. Der französische Mathematiker Jean-Paul Delahaye beschreibt diese Sudoku-Variante in Les ancêtres français du sudoku (als Quelle wird die Zeitschrift Puzzler von 1999 genannt).[8]

Ähnlich mit der Anordnung der Zahlen operiert ein „Skyline-Sudoku“. Hierbei werden die einzutragenden Zahlen als Hochhäuser der entsprechenden Höhe interpretiert. Zur Vorgabe gehören Zahlen am Rand einer Zeile oder Spalte; diese geben an, wie viele Häuser man beim Blick in die Reihe sieht, wenn man sich vorstellt, dass kleinere Häuser (also Zahlen) von davorstehenden größeren verdeckt werden.

Buchstaben-, Silben- und Wörter-Sudoku

Buchstaben-, Silben- und Wörter-Sudokus werden zum Lesen- und Schreibenlernen in der Grundschule eingesetzt. Durch das wiederholende Lesen und Schreiben der Buchstaben, Silben oder Wörter prägen sich die Schüler Laute, Lautgruppen, Buchstaben, Silben und Wörter ein.[9]

Rechen-Sudoku

Rechen-Sudokus werden zum Rechnenlernen in der Grundschule eingesetzt. Erst durch das Ausrechnen der Plus-, Minus-, Mal- und Teilaufgaben in den Kästchen der 4×4-, 6×6- und 9×9-Sudokus erhält man die jeweiligen Sudoku-Startzahlen. Die so errechneten Sudoku-Startzahlen trägt man nach den üblichen Sudoku-Regeln in die leeren Kästchen des Sudoku-Feldes ein.[10]

Farben-Sudoku

Bei Farben-Sudokus dürfen zusätzlich zu den bestehenden Regeln in allen Feldern gleicher Farbe keine Zahlen doppelt vorkommen.

Rechtschreib-Sudoku

Rechtschreib-Sudokus werden zum Lernen der wichtigsten Rechtschreibregeln in der Grundschule eingesetzt. Durch das wiederholende Schreiben der Wörter mit einer Rechtschreibbesonderheit (zum Beispiel doppelter Konsonant, Auslautverhärtung, ß, ä-e/äu-eu, Dehnungs-h und so weiter) in die 4×4-, 6×6- und 9×9-Felder prägen sich die Schüler die Wörter mit den jeweiligen Rechtschreibbesonderheiten ein. Um die Sudokus richtig zu lösen, müssen die Kinder einen „merk“-würdigen Start-Satz immer wieder lesen, leise vorsprechen und nach den typischen Sudoku-Regeln in die Kästchen schreiben (Dehnungs-h-Startsatz eines 4×4-Sudokus: „Ihrer Uhr fehlen Zahlen.“).[11]

Regeln und Begriffe

Das Standard-Sudoku besteht aus einem Gitterfeld mit 3×3 Blöcken, die jeweils in 3×3 Felder unterteilt sind, insgesamt 81 Felder in 9 Zeilen und 9 Spalten. In einige dieser Felder sind schon zu Beginn Ziffern zwischen 1 und 9 eingetragen („Vorgaben“).

Die Aufgabe besteht darin, die leeren Felder des Rätsels so zu füllen, dass in jeder der je neun Zeilen, Spalten und Blöcke jede Ziffer von 1 bis 9 nur einmal auftritt.

Die drei Bereiche (Zeile, Spalte, Block) sind gleichrangige „Einheiten“ oder Gruppen.

Während des Lösungsprozesses stehen in jedem Feld noch mehrere den Regeln konforme Lösungsziffern als „Kandidaten“ imaginär zur Verfügung, die man notieren kann und die man schrittweise eliminiert.

Da jede Lösungszahl immer drei Einheiten (Zeile, Spalte, Block) zugleich angehört, bewirkt sie in diesen direkte Ausschlüsse („Sperren“). Solche Sperren entstehen zusätzlich durch logische Schlüsse aus besonderen Anordnungen von Kandidaten (siehe unter Lösungsmethoden/globale Paarsuche).

Obwohl Sudokus in der Regel mit Ziffern arbeiten, sind zur Lösung keinerlei Rechenkenntnisse erforderlich; man könnte ebenso neun andere abstrakte Symbole verwenden – Ziffern ermöglichen durch ihre feste und bekannte Reihenfolge jedoch ein leichteres Überprüfen der fehlenden Elemente innerhalb einer Einheit.

Ein Sudoku mit Buchstaben heißt Mojidoku. Hexadoku nannte die Elektronikzeitschrift elektor ihr monatliches 4×4-Sudoku, bestehend aus den 16 Hexadezimalziffern 0–9 und A–F, beziehungsweise Alphadoku eine 5×5-Sudoku-Variante für die 25 Buchstaben A–Y oder Anumski eine 6×6-Variante, die mit allen 36 alphanumerischen Werten zu befüllen war.

Lösungsmethoden

Analytisch-systematische Basismethoden

1. Methode „Sichten“: Nimm eine häufige Ziffer, zum Beispiel „5“. Auf den roten Linien sind weitere „5“er verboten. Die einzige freie Position im oberen rechten Block für eine „5“ ist somit das grün markierte Feld. 2. Methode „Durchzählen“: Für das blau markierte Feld in der Mitte scheiden alle bereits vorgegebenen Ziffern in der Zeile und Spalte (alle blau eingerahmt) aus, im Block gibt es keine weitere. Somit bleibt nur Kandidat „5“ für dieses Feld.

Zur Lösung von Sudokus sind systematisches Vorgehen, Analyse und logisches Denken gefordert. Leichte Sudokus lassen sich oft im Kopf durch logisches Denken lösen. Für anspruchsvollere Rätsel werden unter Umständen Notizen benötigt, um verschiedene Lösungsmöglichkeiten je Feld (Kandidaten) festzuhalten.

Im Folgenden sei als analytisch-systematische Lösung eines Sudokus die Kombination von Methoden verstanden, die nach einer relativ kurzen, übersichtlichen Untersuchung zu einem eindeutigen Ergebnis für eine bisher ungesetzte Position führen. Beispiele für solche Methoden sind: Sichten (Scannen), Durchzählen, weitere Ausschlussverfahren von Kandidaten. Wenn sich alle Positionen auf diese Weise entscheiden lassen, kommt man – im Gegensatz zum Probieren (Hypothesenfalsifikation) – garantiert mit einem einzigen Blatt aus.

Sichten von Ziffern

Man wählt zunächst eine Ziffer willkürlich aus und betrachtet anschließend alle bereits mit dieser Ziffer besetzten Felder einzeln nacheinander (Vorgaben und Lösungen). Weitere Felder der jeweiligen Einheit (= Zeile, Spalte oder Block) scheiden per Regel aus. Wenn dadurch in einer beliebigen Einheit alle Felder bis auf eines ausgeschlossen sind, wird die betrachtete Kandidatenziffer im verbliebenen Feld zur Lösung. (Nur eine Position verbleibt für die betrachtete Ziffer.) Anschließend fährt man mit der nächsten Ziffer gleichartig fort.

Durchzählen in Einheiten

„Methode des nackten Einers“: Hierbei wählt man zunächst ein Feld aus. Für dieses werden alle Ziffern ausgeschlossen, die in derselben Einheit (Zeile, Spalte oder Block) bereits stehen. Wenn nur noch eine Ziffer möglich bleibt, ist sie die Lösung für dieses Feld. (Nur eine Ziffer verbleibt für die betrachtete Position.) Zweckmäßigerweise beginnt man in Spalten, Zeilen oder Blöcken mit den wenigsten leeren Feldern, da es hier am wahrscheinlichsten ist, dass man alle Zahlen bis auf eine ausschließen kann.
„Methode des versteckten Einers“: Bei dieser Methode betrachtet man eine Einheit (Zeile, Spalte oder Block) und eine Ziffer, die noch nicht in dieser Einheit eingetragen ist. Da jede Ziffer in einer Einheit genau einmal vorkommt, muss sie in eines der freien Felder eingetragen werden. Falls es nur noch ein freies Feld in dieser Einheit gibt, in die die Ziffer eingetragen werden kann, ohne dass sie in einer anderen Einheit mehrfach vorkommt, wird sie in dieses Feld eingetragen.[12]

Trägt man in jedem Feld (vorläufig) die Ziffern ein, die in den jeweiligen Einheiten (Zeile, Spalte oder Block) noch nicht vorkommen, erkennt man nackte Einer daran, dass in einem Feld nur noch eine Ziffer steht. Beim versteckten Einer steht die betreffende Ziffer in einer Einheit genau einmal.

Weitere Ausschlussverfahren (Eliminierung)

Hierbei handelt es sich um Methoden, die gestatten, die Kandidatenmenge einzelner Felder weiter zu reduzieren. Zweckmäßigerweise beginnt man mit denen, die nur auf eine Einheit angewandt werden. Prinzipiell ist die Reihenfolge ihrer Anwendung vertauschbar.

Die Twin-Methode (Doppelzwilling):
- Die direkte Twin-Methode: Wenn in $n\geq 1$ Feldern einer Einheit (Zeile, Spalte oder Block) nur noch dieselben $n$ Kandidaten alleine stehen, das heißt, wenn die Kandidatenmengen dieser Felder keine weiteren Ziffern mehr enthalten, dann muss in jedem der $n$ Felder eine dieser $n$ Ziffern stehen (außer bei $n=1$ weiß man noch nicht, welche Ziffer in welches Feld gehört). Somit können diese Ziffern in keinem anderen Feld der betroffenen Einheit vorkommen. Liegt für $n>1$ der Doppelzwilling z. B. in einer Zeile, sind die $n$ Ziffern als Kandidaten in den Restfeldern dieser Zeile zu tilgen. Analog gilt dies für Spalte oder Block.
  Beim Doppelzwilling / „Doppeltwin“ können sogar zwei Einheiten zugleich bereinigt werden: z. B. Zeile und Block oder Spalte und Block, wie im Beispiel „Bild: Logikmuster A“ – Beispiel grün – dargestellt ist. Hier kann z. B. weder die 5 noch die 9 in dem grün unterlegten Bereich vorkommen.
- Die indirekte (versteckte) Twin-Methode: Wieder betrachtet man eine Einheit und sucht $n\geq 1$ Zahlen, die nur noch in genau $n$ Feldern dieser Einheit stehen, das heißt, keine dieser Zahlen kommt in einer anderen Kandidatenmenge in dieser betrachteten Einheit vor. Dann gilt, dass in jedem der $n$ Felder eine dieser $n$ Zahlen stehen muss und man kann alle anderen Kandidaten aus diesen $n$ Feldern streichen. Ein Beispiel für $n=1$ ist im Bild „mit allen verbliebenen Kandidaten“ in der Zeile 8 das Feld g8 mit den Ziffern 3 und 6, eine Konstellation, die die Ziffer 3 aus diesem Feld verdrängt; oder für $n=2$ die Spalte f mit den Feldern f1 und f9 und den Ziffern 6 und 8.
  Durch diese Tilgung wird der indirekte Twin zum direkten Twin und es werden die dort beschriebenen Kandidatenlöschungen möglich.
Methode des nackten Triples (Drilling): Sie stellt eine Analogie zur direkten Twin-Methode dar. Kommen in $n\geq 2$ Feldern einer Einheit nur $n$ Ziffern als Kandidaten vor (das kann auch bei $n\geq 3$ bis herab zum Ziffernpaar pro Feld sein; eine Konstellation, die auch „Schwertfisch“ (= swordfish) genannt wird), so sind diese $n$ Ziffern aus anderen Feldern derselben Einheit (Zeile, Spalte oder Block) zu tilgen. Ein Beispiel sind in der Spalte f die Felder f5 und f7, wodurch die zwei Kandidaten 3 und 7 in allen anderen Feldern dieser Spalte gelöscht werden. Auf diese Weise werden bei jedem Eliminationsschritt pro Einheit disjunkte Kandidatenlisten gebildet; im Beispiel die Ziffern 1 und 4 in den Feldern f4 und f6.
Beim Doppeltriple befinden sich die $n\leq 3$ betrachteten Felder nicht nur in einer Zeile oder Spalte, sondern zugleich im selben Block. Dann können diese Kandidaten nicht nur in den restlichen Feldern derselben Zeile oder Spalte, sondern auch im Block getilgt werden (Beispiel: Kandidaten 3, 5, 7 auf den Feldern d7–f7 in der Zeile 7 und im Block d7–f9 in Bild „mit allen verbliebenen Kandidaten“).
Der „Schwertfisch“ (= swordfish, s. auch oben): Dieses Konstrukt ist der direkten Twin-Methode sehr verwandt, nur handelt es sich um paarweise Felder in nicht nur 2, sondern in 3 Zeilen/Spalten, bei denen jeweils genau ein Endpunkt in der Spalte/Zeile paarweise mit einem Endpunkt eines anderen Paares in der Spalte/Zeile übereinstimmt, so dass die Endpunkte des Ganzen eine geschlossene Ringfigur darstellen. Auch in einem solchen Falle ist die betreffende Kandidatenziffer in den betroffenen 3 Spalten/Zeilen für die verbliebenen jeweils 7 anderen Felder der Spalte/Zeile ausgeschlossen.
Die X-Wing-Methode: Voraussetzung hierfür ist eine paarige Anordnung nur eines Kandidaten in zwei Einheiten:
- symmetrischer X-Wing: In zwei Zeilen (oder Spalten) kommt eine Kandidatenziffer ausschließlich in zwei identischen Spalten (beziehungsweise Zeilen) vor. Diese 4 Felder müssen in mindestens 2 verschiedenen, können aber auch in 4 Blöcken liegen. Diese vier möglichen Treffer-Zellen stellen Ecken eines imaginären Rechtecks dar beziehungsweise bilden ein symmetrisches X-Muster. Die wahren Lösungstreffer müssen zwingend an den Enden einer der beiden möglichen Diagonalen liegen. Folglich muss dieser Kandidat in den verbleibenden 2*7 Feldern der zwei Spalten (beziehungsweise Zeilen) und in den restlichen Feldern gemeinsamer Blöcke eliminiert werden.
- asymmetrischer X-Wing (Typ A): In zwei Zeilen (oder Spalten) kommt eine Kandidatenziffer nur zweimal vor. Jeweils eine aus beiden Zeilen (Spalten) liegt in derselben Spalte (Zeile), die beiden verbleibenden liegen in einem gemeinsamen Block. Hierbei entsteht eine asymmetrische X-Figur. Die Enden der möglichen beiden Diagonalen bilden Eckpunkte eines Trapezes. Das bewirkt einen Kandidatenausschluss in den verbleibenden 7 Feldern der einen gemeinsamen Spalte (oder Zeile) beziehungsweise der gemeinsamen Blöcke (siehe Bild: Logikmuster B Beispiel rot und gelb).
- asymmetrischer X-Wing (Typ B): In zwei Zeilen (oder Spalten) kommt eine Kandidatenziffer nur zweimal vor. Dennoch liege keine paarige Position in einer Spalte (Zeile) vor, sondern je zwei liegen in denselben Blöcken. Auch hierbei entsteht eine X-Figur. Die Enden der möglichen beiden Diagonalen bilden Eckpunkte eines Trapezes. Das bewirkt einen Kandidatenausschluss in den verbleibenden 7 Feldern der gemeinsamen Blöcke.
- asymmetrischer X-Wing (Typ C): In zwei Blöcken kommt eine Kandidatenziffer jeweils nur zweimal vor. Je ein Kandidat liegt in derselben Zeile (oder Spalte). Hierbei bilden die möglichen Treffer ebenfalls ein Trapez. Es bewirkt einen Kandidatenausschluss in den beiden verbleibenden 7 Feldern der beiden gemeinsamen Zeilen (Spalten) (siehe Bild: Logikmuster B Beispiel rot und gelb).
Block-Interaktion: Ist ein Zahlenkandidat in zwei horizontal (oder vertikal) angeordneten Blöcken in einer (!) gemeinsamen Zeile (beziehungsweise Spalte) zweier Blöcke ausgeschlossen (ohne in den drei betrachteten Blöcken bereits als Lösung eingetragen zu sein), so muss er in diesem verbleibenden Block in dieser Zeile als Lösung erscheinen, ist damit in den zwei verbleibenden Zeilen (beziehungsweise Spalten) dieses Blocks ausgeschlossen (vergleiche Bild: Logikmuster C Beispiel rosa; obwohl dort Paare betrachtet wurden, gilt dies auch für jeden einzelnen Kandidaten).
Block-Reihe-Check: Wenn in einem Block eine Kandidatenziffer zwar noch nicht eindeutig einem Feld zugeordnet werden kann, aber alle Felder des Blocks, in welcher diese Ziffer noch möglich ist, in ein und derselben Reihe (das heißt Zeile oder Spalte) liegen, dann verdrängt die Kandidatenziffer alle ihre anderen Vorkommen in der jeweiligen Reihe außerhalb des Blocks. Ein Beispiel für „Block-zu-Zeile-Check“ ist die Situation in Block d1–f3: Dort kommt die Kandidatenziffer 6 in diesem Block nur (noch) in der Zeile 1 vor. Sie muss also in dieser Zeile für diesen Block bspw. im Feld d1 oder Feld f1 gesetzt werden, und kann damit nicht außerhalb dieses Blocks in der Zeile 1 vorkommen, bspw. in den Feldern a1–c1 oder g1–i1. Entsprechend gibt es einen „Block-zu-Spalte-Check“ in Block d4-f6 mit den Feldern d4 und d6 und der Kandidatenziffer 9 (die allerdings in der Spalte d außerhalb des Blocks d4-f6 anderweitig schon verdrängt ist).

Globale Paarsuche (GPS)

Unter allen veröffentlichten Sudokus haben 75 Prozent einen leichten, mittleren oder schweren Schwierigkeitsgrad. Die GPS-Methode führt bei ihnen zur kompletten Auflösung des Sudokus. Die restlichen 25 Prozent sind sehr schwierig und können nur mit einer Abwandlung dieser Methode und alternativen Strategien gelöst werden.

Grundsatz

Diese spezielle Methode ist als Kreislauf zu verstehen: Zuerst besondere Kandidaten suchen, dann aus diesen Kandidaten Schlussfolgerungen ziehen und anschließend auf erneute Kandidatensuche gehen. Die globale Paarsuche liefert die wertvollsten Kandidaten. Es wird keine gewöhnliche Kandidatenliste erstellt, weil sie zumeist unübersichtlich ist und die Sicht auf schnelle Schlussfolgerungen verschließt. Die folgenden Konsequenzen beruhen auf einer Sammlung von Logikregeln:

Auf eine unkomplizierte Art werden Kandidatenpaare ermittelt.
Es folgt die Anwendung von 6 Logikregeln. Dadurch werden gesperrte Einheiten ermittelt.
Durch Schritt 2 ist die Menge an Möglichkeiten eingeschränkt worden. Bei der erneuten Kandidatensuche werden weitere Pärchen gefunden.
Und wieder werden (die gleichen) 6 Logikregeln angewendet.

Die Kandidatenmenge reduziert sich schnell und Lösungszahlen werden ermittelt. Die Schritte können beliebig wiederholt werden. Dabei kann nach Belieben zwischen Ziffern und Einheiten sowie zwischen Kandidatensuche und deren Auswertung „gesprungen“ werden – diese Methode ist nicht starr. Weder die Kandidatensuche noch deren Auswertung muss an irgendeiner Stelle vollständig sein. Man kann sich „treiben lassen“ und das Sudoku scheinbar „chaotisch“ lösen.

Einzige Bedingung ist die Einhaltung der Kausalkette: Kandidatenpaare sperren Einheiten, gesperrte Einheiten reduzieren die Kandidatenmenge.

Anleitung

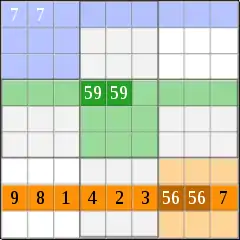
Logikmuster A: Kandidatenpaare (weiß) sperren andere Einheiten.
Lösungszahlen: schwarz

Schritt 1: Verschiedene Lösungszahlen sind im Sudoku vorgegeben. Jede dieser Lösungszahlen belegt 3 Einheiten (Spalte, Zeile, Block). Da in jeder dieser 3 Einheiten diese Lösungszahl nur dieses eine Mal vorkommen darf, sind alle 3 Einheiten für weitere Einträge derselben Zahl „gesperrt“.

Betrachte alle Zeilen und Spalten, die durch die Lösungszahlen gesperrt werden. Diese Zeilen und Spalten kreuzen Blöcke, die diese Lösungszahlen noch nicht enthalten. Ermittle alle Kandidaten, die dadurch in diesen Blöcken entstehen (siehe auch „scannen“). Trage aber nur

neue Lösungszahlen und
Kandidatenpaare ein.

Gibt es für eine Ziffer 3 oder mehr Kandidaten, lasse sie weg. Die Reihenfolge deiner Suche ist in jedem Fall unwichtig, ebenso die Vollständigkeit. Allerdings: Je schwieriger das Sudoku ist, desto mehr Paare werden benötigt.

Schritt 2: Wurden genügend Kandidatenpaare ermittelt, benutze alle logischen Schlüsse, die du aus den Paaren ziehen kannst. Wenn du etwas nicht verstehst, lasse es weg. Allerdings: Je schwieriger das Sudoku ist, desto mehr logische Schlüsse werden benötigt.

Logikregel 1 (siehe Logikmuster A – Blau): Ein einfaches Kandidatenpaar sperrt je nach Anordnung 1-2 Einheiten.

im Beispiel sperrt das „7“-Paar die blaue Zeile und den blauen Block (also 2 Einheiten)
damit kann in beiden Einheiten keine weitere „7“ mehr stehen.

Logikregel 2 (siehe Logikmuster A – Grün): Doppelpaare belegen immer genau 2 Felder einer Einheit. Doppelpaare sperren damit je nach Anordnung 1-2 Einheiten UND 2 Felder.

im Beispiel sperrt das „59“-Doppelpaar die grüne Zeile und den grünen Block (also 2 Einheiten),
damit kann in beiden Einheiten an keiner anderen Stelle eine „5“ oder eine „9“ stehen.
Das „59“-Doppelpaar belegt 2 Felder – diese 2 Felder können durch keine andere Ziffer belegt werden,
damit sind nicht nur 2 Einheiten gesperrt, sondern auch diese 2 Felder in jeder dieser Einheiten.

Logikregel 3 (siehe Logikmuster A – Orange): Sind in einer Einheit 7 Lösungszahlen vorhanden, werden damit die fehlenden 2 Ziffern festgelegt. Diese fehlenden 2 Ziffern bilden ein Doppelpaar und sperren je nach Anordnung 1-2 Einheiten UND 2 Felder.

Im Beispiel fehlen in der orangefarbenen Zeile nur die „5“ und die „6“,
es entsteht ein Doppelpaar,
dieses Doppelpaar belegt genau 2 Felder – in der orangefarbenen Zeile und im orangefarbenen Block,
dadurch können die „5“ und die „6“ im orangefarbenen Block auch nur in genau diesen 2 Feldern vorkommen,
keine andere Ziffer kann in diesen 2 Feldern stehen.

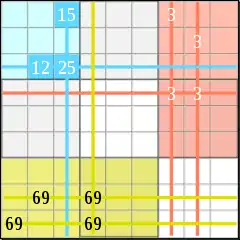
Logikmuster B: Kandidatenpaare (weiß) sperren andere Einheiten

Logikregel 4 (siehe Logikmuster B – Rot): Sind Einheiten mit gleichen Kandidaten paarweise angeordnet, werden 4-6 Einheiten gesperrt. Im Beispiel ist ein Spalten-Paar zu sehen.

Beide roten Blöcke enthalten jeweils ein „3“-Paar,
beide Paare sind so angeordnet, dass sie zugleich in den gleichen Spalten stehen,
damit sind nicht nur die roten Blöcke, sondern auch die 2 roten Spalten gesperrt,
die Sperrung der roten Zeile ergibt sich aus „Logikregel 1“,
damit sind in unserem Beispiel 5 Einheiten gesperrt; in diesen Einheiten kann keine weitere „3“ vorkommen.

Logikregel 5 (siehe Logikmuster B – Gelb): Doppelpaare belegen immer genau 2 Felder einer Einheit. Sind Einheiten mit gleichen Doppelpaaren paarweise angeordnet, werden 4-6 Einheiten gesperrt UND 4 Felder. Im Beispiel ist ein Zeilen-Doppel-Paar zu sehen.

Beide gelben Blöcke enthalten ein „69“-Doppelpaar,
beide Doppel-Paare sind so angeordnet, dass sie zugleich in den gleichen Zeilen stehen,
damit sind nicht nur die gelben Blöcke, sondern auch die 2 gelben Zeilen gesperrt,
die Sperrung der gelben Spalte ergibt sich aus „Logikregel 2“,
jedes „69“-Doppelpaar belegt 2 Felder in jedem gelben Block – diese Felder können durch keine andere Ziffer belegt werden,
damit sind in unserem Beispiel nicht nur 5 Einheiten gesperrt, sondern auch 4 Felder.

Logikregel 6 (siehe Logikmuster B – Türkis): Triples können aus 3 „verschränkten“ Paaren entstehen. Ein Triple sperrt je nach Anordnung 1-3 Einheiten und 3 Felder.

Im Beispiel sperrt das „5“-Paar die türkisfarbene Spalte,
das „2“-Paar sperrt die türkisfarbene Zeile,
das Triple belegt genau 3 Felder des türkisfarbenen Blocks,
in diesen 3 Feldern kann keine andere Ziffer stehen.

Schritt 3 (und so weiter): Kandidatenpaare sperren Einheiten. Nachdem du diese Sperren ermittelt hast, beginnst du die „zweite Runde“. Wiederhole deine Suche nach Kandidaten. Durch die gefundenen Sperren wirst du neue Kandidatenpaare finden.

Dabei wird es häufig vorkommen, dass du neue Kandidatenpaare findest, die „alte“ Paare kreuzen. Dabei ergibt sich mindestens eine Lösungszahl.

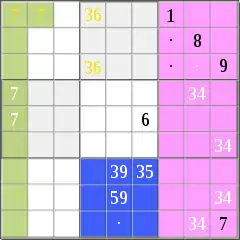
Logikmuster C: Kandidatenpaare (weiß) haben Auswirkungen auf andere Kandidatenpaare (gelb). Lösungszahlen: schwarz

Beispiel 1 (Logikmuster C – Grün):

Du siehst ein „7“-Paar (gelb), das zuerst ermittelt wurde,
später ermittelst du ein anderes „7“-Paar (weiß),
das weiße „7“-Paar erzeugt eine Sperre, bei der die linke Ziffer des alten (gelben) Paares gestrichen werden muss,
übrig bleibt die Lösungszahl; diese hat weitere Konsequenzen…

Beispiel 2 (Logikmuster C – Blau):

Du siehst oberhalb der blauen Einheit ein „36“-Doppelpaar (gelb), das zuerst ermittelt wurde,
später ermittelst du in der blauen Einheit ein „359“-Triple (weiß),
die Konsequenz aus dem Triple ist in „Logikregel 6“ beschrieben; damit gibt es in der blauen Einheit nur noch 6 freie Felder (für die Ziffern „124678“),
betrachte oberhalb der blauen Einheit die Lösungszahl „6“,
bedingt durch die Sperren aus Doppelpaar, Lösungszahl und Triple kann die „6“ in der blauen Einheit nur an der mit dem weißen Punkt markierten Stelle stehen; dies hat weitere Konsequenzen…

Beispiel 3 (Logikmuster C – Rosa):

Du siehst 3 Lösungszahlen,
du ermittelst in 2 Einheiten „34“-Doppelpaare, die paarweise angeordnet sind (spaltenweise),
die Konsequenz aus den Doppelpaaren ist in „Logikregel 5“ beschrieben,
damit entsteht im oberen rosafarbenen Block ein neues Doppelpaar: Die „3“ und die „4“ kann nur in den mit den schwarzen Punkten markierten Feldern stehen,
außerdem entsteht eine weitere Konsequenz: Im oberen rosafarbenen Block kann an der mit dem weißen Punkt markierten Stelle nur eine „7“ stehen (betrachte hierzu die anderen Einheiten des Sudoku).

Nachtrag

Nur bei sehr schwierigen Sudokus muss diese Methode ergänzt werden. Es empfiehlt sich dann, nicht nur Paare, sondern auch Dreier zu suchen. Sollte dies auch nicht ausreichen oder die Kandidatenliste zu unübersichtlich werden, müssen bekannte andere Lösungsstrategien zu Hilfe genommen werden.

Falsifikation einer Hypothese

Die Hypothese (oder: Was-wäre-wenn?, Ariadnes Faden, Backtracking) sollte erst dann angewendet werden, wenn alle oben dargestellten Methoden nicht mehr weiterhelfen. Aber auch hier ist es hilfreich, nicht wahllos vorzugehen. Wenn man sich nicht die Mühe machen will, die Hypothese auf einem getrennten Blatt auszuprobieren, kann man die bisherigen, eindeutigen Treffer mit Kugelschreiber und die hypothetischen Ziffern mit Bleistift eintragen, um die Ausgangssituation im Fall einer falschen Hypothese wiederfinden zu können.

Für das Ausprobieren scheinen sich vor allem Zellen zu eignen, die nur zwei Kandidaten aufweisen, weil eine fehlerhafte Hypothese automatisch die Alternative als richtig bestätigt (sofern das Sudoku als eindeutig lösbar angesehen werden darf). Mehrstufige Hypothesenfolgen, die dadurch entstehen, dass beide Alternativen fehlerfrei erscheinen und man eine weitere Hypothese für ein weiteres Feld aufstellen muss, sind nur schwierig zu lösen und zudem mit der Unsicherheit behaftet, dass sich erst im weiteren herausstellen wird, dass bereits im ersten Schritt eine falsche Variante gewählt wurde. Deshalb empfiehlt es sich, zum Ausgang zurückzukehren und bereits für die erste Alternativprüfung ein völlig anderes Feld heranzuziehen.

Das Auffinden einer Lösung auf diesem Weg reicht nicht aus als Beweis für die eindeutige Lösbarkeit. Um diese zu zeigen, müssen alle Alternativen zum gefundenen Lösungsweg als Irrwege nachgewiesen werden.

Backtracking mit Brute Force

Auf dem Computer kann man ein Sudoku mit der Backtracking-Methode lösen. Beginnend mit dem ersten freien Feld, probiert man systematisch, mit der Eins beginnend, ob man zu einer Lösung kommt. Beim ersten Widerspruch geht man zurück (englisch backtrack). Dieser Lösungsweg lässt sich sehr elegant rekursiv formulieren und man ist sicher, dass alle Kombinationsmöglichkeiten abgesucht werden. Da es sich um tausende Wege handeln kann, ist dieser Algorithmus nur für Computerprogramme geeignet. Der Lösungsalgorithmus ist allerdings nicht der Schnellste, da er keinerlei analytische Vorinformationen verwendet und nur durch Ausprobieren vorgeht. Er setzt also mit roher Gewalt (englisch brute force) Ziffern ein und überprüft diese dann. Dennoch erhält man auf gewöhnlichen PCs auch für schwierige 9×9-Sudokus meist zügig die Lösung. Dabei hängt die Programmlaufzeit entscheidend von der Anzahl der vorgegebenen Ziffern ab. Auch die festgelegte Reihenfolge, in der die Felder gefüllt werden, beeinflusst die Programmlaufzeit. Bei größeren Sudokus stößt diese Methode jedoch schnell an ihre Grenzen.

Backtracking mit dynamischer Reihenfolge

Man kann die Backtracking mit Brute-Force-Methode dahingehend modifizieren, dass die Bearbeitungsreihenfolge der Felder dynamisch generiert wird. Anstatt das erste freie Feld zu belegen, bestimmt man jenes mit der geringsten Anzahl an Kandidaten und beginnt dort mit dem versuchsweisen Einsetzen. Damit reduziert sich der Aufwand auf ungefähr lineare Laufzeit, da in der Praxis (auch bei schwierigen Sudokus) fast immer ein Feld existiert, für das nur eine Zahl in Frage kommt. Da die Reihenfolge, in der die Felder befüllt werden aber nicht festgelegt ist, muss bei jedem Schritt der momentane Zustand gespeichert werden, um diesen gegebenenfalls später noch einmal reproduzieren zu können.

Logische Suche

Man kann auch menschliche Vorgehensweisen algorithmisch umsetzen. Dazu sucht man zum Beispiel in einem ersten Schritt Felder mit nur einem Kandidaten. In einem weiteren Schritt sucht man Ziffern, die in einer Zeile, Spalte oder in einem Block nur in ein Feld passen. Auch möglich ist die Suche nach Paaren oder Tripeln von Kandidaten, die gemeinsam betrachtet werden, um die Kandidatenmengen zu verkleinern. Hierbei werden logische Verknüpfungen zwischen mehreren Feldern gesucht, von denen klar ist, dass bestimmte Zahlen in den Feldern dieser Einheit stehen, wodurch diese Zahlen für die nicht in der Einheit befindlichen Zahlen als Lösungen ausscheiden (Beispiel: {1, 2} {2, 3} {3, 1}; wenn diese Kandidatenmengen zum Beispiel in einer Reihe stehen, ist klar, dass diese Einheit die Zahlen 1, 2 und 3 enthalten muss, wodurch sie aus allen anderen Kandidatenmengen in dieser Reihe ausscheiden). Je schwieriger ein Sudoku lösbar ist, desto mehr unterschiedliche logische Ansätze werden im Programm nötig. Diese sind oft sehr aufwändig in der programmtechnischen Umsetzung.

Exact Cover

Eine mathematische Methode zum Lösen eines Sudoku ist die Behandlung als Problem der exakten Überdeckung (englisch Exact Cover Problem). Aus den vorgegebenen Ziffern lässt sich für jedes Feld eine Menge von Kandidatenziffern bestimmen, die für ein Feld die Schnittmenge aus je drei Mengen ist: Diese sind die Komplemente der jeweils in derselben Zeile, Spalte und im selben Block enthaltenen Ziffern zur Menge aller Ziffern (ohne die Null). In einfachen Fällen hat das Rätsel die Eigenschaft, dass mindestens ein Feld eine einelementige Kandidatenmenge besitzt, oder dass ein Element aus einer Kandidatenmenge eines Feldes nicht in den Kandidatenmengen aller anderen Felder derselben Spalte oder Zeile oder desselben Quadrats vorkommt. Dieser Kandidat kann dann fest in das jeweilige Feld eingesetzt werden und die betreffende Ziffer aus den Kandidatenmengen der übrigen Felder in derselben Zeile, Spalte und im selben Quadrat entfernt werden. Dieses Verfahren wird dann solange wiederholt, bis alle Zellen aufgefüllt sind.

$M=\{1\cdots 9\}$ Ziffern
$Z_{1}\cdots Z_{9}$ Mengen der in je einer Zeile enthaltenen Ziffern
$S_{1}\cdots S_{9}$ Mengen der in je einer Spalte enthaltenen Ziffern
$Q_{1,1}\cdots Q_{3,3}$ Mengen der je in einem Teilquadrat enthaltenen Ziffern

Die Kandidatenmenge $K_{i,j}$ eines Feldes $F_{i,j}$ berechnet sich dann in jedem Iterationsschritt wie folgt:

K_{i,j}=(M\setminus Z_{i})\ \cap \ (M\setminus S_{j})\ \cap \ (M\setminus Q_{\lceil {\frac {i}{3}}\rceil ,\lceil {\frac {j}{3}}\rceil })=M\ \setminus \ (Z_{i}\cup S_{j}\cup Q_{\lceil {\frac {i}{3}}\rceil ,\lceil {\frac {j}{3}}\rceil })

Bei besonders schwierigen Sudokus führt diese Methode allein nicht zur Lösung. In diesen Fällen müssen zum Beispiel Paare oder Tripel gesucht werden. In Lösungsprogrammen wird nach dem Versagen der Exact-Cover-Methode meistens aber nicht mit weiteren logischen Ansätzen gearbeitet, sondern – da es in den meisten Fällen am Ende ökonomischer ist – mit Backtracking mit Brute Force oder mit Backtracking mit dynamischer Reihenfolge. Das heißt, falls in einem Iterationsschritt keine einelementige Kandidatenmenge existiert, kann aus einer der (kleinsten) Kandidatenmengen eine Zahl ausgewählt werden, um eine der mehreren möglichen Lösungen zu erhalten (Versuch-und-Irrtum-Methode). Dazu wird wie beim Backtracking mit dynamischer Reihenfolge eine Sicherheitskopie angelegt. Im Fall des Irrtums kann dann auf die Sicherheitskopie zurückgegriffen werden. Auch kann die Exact-Cover-Methode als Vereinfachungsalgorithmus verwendet werden. Finden sich so keine eindeutigen Ziffern mehr, hat sich das Sudoku oftmals aber so sehr vereinfacht, dass die Lösung mittels Brute-Force-Methode in Sekundenbruchteilen zu einer Lösung führt.

Lösungshilfen: Kandidaten-Notation

Die „Uhrzeigerstrichmethode“

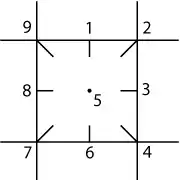
Uhrzeigerstrichmethode: Eine Darstellung für mögliche Lösungen

Da die Sudokus in Zeitungen und Magazinen häufig sehr klein abgedruckt sind, ist die Uhrzeigerstrichmethode hilfreich, die Kandidaten für ein Feld festzuhalten. Man macht im Feld einen kleinen Strich an der Stelle des „Uhrzeigers“ (siehe Bild). Die Fünf stellt eine Ausnahme dar; sie wird als kleiner Punkt in der Mitte dargestellt. So kann man sich mehrere Kandidaten für ein Feld merken. Wenn man keinen Radiergummi zur Hand hat, kann man einen Kandidatenstrich einfach durchstreichen, wenn weitere Überlegungen diesen ausschließen. Diese Methode ist leichter lesbar als das Schreiben von kleinen Zahlen.

Punkte für Kandidaten setzen

Man kann sehr gut kleine Punkte entsprechend einer Telefontastatur setzen und damit mögliche Kandidaten für ein Feld notieren. Man beginnt mit einem Punkt für die Eins in der linken oberen Ecke, oben in der Mitte kommt der Punkt für eine Zwei, in der rechten oberen Ecke der Punkt für eine Drei, am linken Rand in der Mitte liegt der Punkt für eine Vier und so weiter bis zum Punkt für eine Neun, der dann in der rechten unteren Ecke steht.

Unsichere Zahlen markieren

„Zahlen trage ich nur mit Bleistift ein, um sie notfalls wieder wegradieren zu können. Eine unsichere Zahl markiere ich mit einem Sternchen, alle nachfolgenden dann mit einem Punkt. Taucht später ein Fehler auf, kann ich alle markierten Zahlen wegradieren und an der Sternchen-Stelle neu ansetzen“, empfiehlt Kerstin Wöge aus Spandau, die erste Sudoku-Meisterin, in der B.Z. vom 29. November 2005.

Eine darüber hinausgehende Variante ermöglicht das hintereinandergeschaltete Abarbeiten von Hypothesen mit rekursivem Backtracking: Die erste Auswahl einer unsicheren Ziffer wird z. B. mit einem Dreieck umrandet, alle nachfolgenden erhalten ein kleines Dreieck neben der Ziffer. Wird das Rätsel auf diese Art noch nicht vollständig gelöst und bleibt erneut nur die Wahl einer – weiteren – Hypothese, wird die neue unsichere Ziffer z. B. mit einem Kreis umrandet; alle nachfolgenden erhalten einen kleinen Kreis neben der Ziffer. Läuft man in eine Sackgasse, werden nun nur die zuletzt eingetragenen und mit demselben Symbol versehenen Ziffern ausradiert und die mit dem Kreis umrandete Ziffer durch eine andere Kandidatenziffer ersetzt. Sind auf diese Weise alle Kandidaten für die mit der Kreisumrandung markierten Zellen abgearbeitet, ohne dass eine Lösung erzielt werden konnte, werden nun alle mit einem Dreieck markierten Ziffern ausradiert und die mit dem Dreieck umrandete Ziffer durch einen anderen Kandidaten ersetzt. Mit weiteren Symbolen lassen sich quasi beliebig viele Hypothesen hintereinanderschalten. Einziger Nachteil: Papier hält vielfachem Radieren nicht lange stand!

Mögliche Ziffern mit Farbe eintragen

Man verwendet für jede mögliche Ziffer, die in einem Feld stehen kann, eine andere Farbe. Dadurch ist auf einen Blick ersichtlich, ob in einer Spalte, einer Zeile oder in einem 3×3 Block eine Farbe und somit eine Ziffer nur noch einmal vorkommt. Auch Zweier- und Dreierkombinationen sind dadurch besser auszumachen. Wenn für eine Ziffer immer die gleiche Farbe verwendet wird, genügt es nach einiger Übung, nur noch Farbpunkte platziert zu setzen.

Erstellung neuer Sudokus

Schwieriger als das Lösen eines Sudoku ist dessen Erstellung.

Lösbarkeit: Es muss eine Lösung existieren. Die vorgegebenen Ziffern dürfen nicht zu einem Widerspruch führen.
Eindeutige Lösung: Es darf nur eine Lösung existieren.
Gewünschter Schwierigkeitsgrad: Die Anzahl der vorgegebenen Ziffern bestimmt nicht allein den Schwierigkeitsgrad. Die Anordnung spielt eine entscheidende Rolle.

Algorithmus

Belegung des gelösten Sudokus erstellen
- 1. Weg: Ein leeres Sudokufeld wird Zelle für Zelle durch „Auswürfeln“ (Zufallsgenerator) mit Ziffern befüllt. Sobald es zu einem Regelverstoß kommt, muss per Backtracking-Methode eine andere Belegung probiert werden. Dies ist weniger trivial als beim Lösen des Sudokus: Da eine möglichst „zufällige“ Belegung des Sudokufeldes benötigt wird, kann man nicht einfach alle Ziffern der Reihe nach durchprobieren. Es hindert aber nicht, alle Ziffern, sobald sie einmal „ausgewürfelt“ wurden, als künftig – für die jeweilige Zelle – gesperrt „abzuhaken“ (in einer Tabelle zu markieren)
- 2. Weg: Neun Einsen ohne Regelverstoß im Puzzlefeld verteilen. Dann neun Zweier, neun Dreier usw. verteilen. Auch hier muss ein Backtracking-Algorithmus angewandt werden.
- 3. Weg: Man füllt eine Zeile oder eine Spalte in beliebiger Reihenfolge mit den erlaubten Ziffern, verschiebt dann mit jeder weiteren Zeile/Spalte die Ziffernfolge, bis man am Schluss alle möglichen Varianten untereinander/nebeneinander in einer n×n-Matrix vorliegen hat. Dies alleine wäre ein äußerst trivial zu lösendes Rätsel, da sich die Ziffernfolgen wiederholen; deswegen sollte man über erlaubte Transformationen diese Matrix nun schrittweise so verändern, dass die Ursprungsziffernfolge sowie die ausgeführten Transformationen nicht mehr nachvollziehbar sind. Erlaubte Transformationen sind z. B. das Spiegeln (vertikal, horizontal, schräg), das Rotieren, das Vertauschen ganzer Zeilen oder Spalten, sofern sie innerhalb eines Mini-Quadrates bleiben, das Vertauschen ganzer Zeilen und Spalten von Miniquadraten, oder das komplette Austauschen zweier Ziffern. Etliche dieser Transformationen hintereinander verwischen (fast) alle Hinweise auf die ursprüngliche Ziffernfolge. Von den hier vorgestellten Erstellungsmethoden ist diese die am wenigsten aufwendige und rechenintensive.
- 4. Weg: Aus einem vorhandenen Sudoku durch Transformation ein „neues“ Sudoku erstellen. Mögliche Transformationen sind etwa das Drehen und Spiegeln des Brettes, die Vertauschung von Zeilen innerhalb eines Blocks oder von ganzen Blöcken, sowie das elementweise Anwenden von Permutationen.
- 5. Weg: Man füllt drei voneinander unabhängige Blöcke eines leeren Sudokufeldes in zufälliger Weise mit den Ziffern 1 bis 9. Damit hat man bereits 27 Vorgabewerte, die ohne Prüfung eines Regelverstoßes gesetzt werden konnten. Unabhängige Blöcke sind zum Beispiel die diagonal liegenden Blöcke 1, 5 und 9 oder 3, 5 und 7, aber auch die Blöcke 2, 4 und 9 oder 1, 6 und 8 sind voneinander unabhängig. Nach dem Auffüllen der unabhängigen Blöcke werden die restlichen freien Zellen per Backtracking-Methode in zufälliger Folge gelöst.
Zur Lösung passendes Sudoku-Rätsel erzeugen
- Wiederum durch „Auswürfeln“ werden je nach Schwierigkeitsgrad eine Anzahl Ziffern wieder entfernt (typischerweise so, das zwischen 22 und 36 Ziffern verbleiben). Ohne weitere Kontrolle kann es hierbei aber passieren, dass das Rätsel trivial (langweilig) oder nicht mehr eindeutig lösbar wird.
- Dabei können auch andere Varianten zum Zug kommen. Wie das Beispiel einer Freeware (RedMill Sudoku Resolver) aufzeigt, wird für das Generieren von Sudokus eine geringe Anzahl Zufallszahlen zufällig, jedoch unter Einhaltung der Regeln im Spielfeld verteilt und das Sudoku fertig gerechnet. Bei der Berechnung wird zuerst solange nach Feldern mit nur einer Möglichkeit gesucht, bis keine solche Felder mehr vorhanden sind. Wird das Sudoku dadurch nicht aufgelöst, wird eine Kopie des Spiels erstellt um die Backtracking-Methode zu ermöglichen. Durch das Backtracking können Annahmen getestet werden. Mit Wechselwirkung der Annahmen und der Absuche der Felder mit nur einer Möglichkeit wird das Sudoku fertig gerechnet. Geht das Sudoku nicht auf, wird die vorherige Kopie des Spiels verwendet und eine andere Annahme getestet. Geht das Sudoku auf keinen Fall auf, wird die erste Kopie verwendet und darin eine der Zufallszahlen gelöscht und das Ganze wiederholt. Am Ende wird per Zufallszahl, je nach Schwierigkeitsgrad, Zahlen im fertig gerechneten Sudoku gelöscht und angezeigt, wie dies oben beschrieben ist. Das im Hintergrund fertig gerechnete Sudoku wird dabei als Schattenkopie für Spielhilfen verwendet.

Die Mathematik hinter Sudoku

Die Anzahl der Sudokus

Abbildung 3a. Sudoku aus Abb. 1 mit Farben anstatt Ziffern

Um alle denkbaren, vollständig ausgefüllten 9×9 Standard-Sudokus zu erzeugen, könnte man wie folgt vorgehen: man beginnt mit einem leeren 9×9-Gitter und setzt nun zeilenweise von links nach rechts die Ziffern ein. Für das erste Feld in der ersten Zeile hat man offenbar 9 Möglichkeiten, für das zweite 8, das dritte 7 usw. Insgesamt ergeben sich für die erste Zeile 9! (d. h. 9 Fakultät) Möglichkeiten. Wenn man in den verbleibenden 8 Zeilen ebenso vorgeht, erzeugt man mithin (9!)⁹ ≈ 1,1 ⋅ 10⁵⁰ verschiedene 9×9-Gitter. Da allerdings unberücksichtigt blieb, dass jede Ziffer auch in jeder Spalte und in jedem Block nur genau einmal auftreten darf, hat man bei einem solchen Vorgehen (sehr) viele 9×9-Gitter erzeugt, die keine vollständig ausgefüllten 9×9 Standard-Sudokus darstellen. Bertram Felgenhauer und Frazer Jarvis konnten 2005 zeigen, dass es (nur) 6.670.903.752.021.072.936.960 (ca. 6,7 Trilliarden oder 6,7 ⋅ 10²¹) verschiedene (vollständig ausgefüllte) 9×9 Standard-Sudokus gibt.[13]

Allerdings unterscheiden diese sich untereinander nicht unbedingt wesentlich: wenn man beispielsweise in einem vollständig ausgefüllten Sudoku die Einsen und Zweien vertauscht, so bleibt das Sudoku letztlich dasselbe. Tatsächlich ist es unerheblich, ob man ein Sudoku-Feld mit Ziffern, Symbolen oder Farben ausfüllt. Abbildung 3a etwa gibt das Sudoku aus Abbildung 1 wieder – nur mit Farben anstatt Ziffern. Ein Sudoku lösen heißt in diesem Sinne, die 9×9 Felder des Spielfelds in 9 (Farb-)Mengen von jeweils 9 Feldern zu partitionieren, so dass für die 9 Felder in einer (Farb-)Menge gilt: keine zwei sind in ein und derselben Reihe, Spalte oder Block enthalten. Auch wenn man beispielsweise die erste und die zweite Zeile vertauscht, vergleiche Abbildung 3b, erhält man ein grundsätzlich identisches Sudoku: Um etwa das ursprüngliche zu lösen, könnte man genauso gut dasjenige mit den vertauschten Zeilen lösen und am Ende die beiden Zeilen wieder zurücktauschen. Entsprechend kann man bestimmte Spalten vertauschen oder die drei oberen Blöcke mit den drei unteren vertauschen oder das Spielfeld drehen oder spiegeln, vergleiche Abbildungen 3cde.

Abbildung 3b. Sudoku aus Abb. 1 mit Farben anstatt Ziffern und vertauschten ersten beiden Zeilen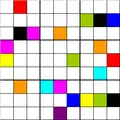
Abbildung 3c. Sudoku aus Abb. 1 mit Farben anstatt Ziffern und vertauschter zweiter und dritter Blockspalte
Abbildung 3d. Sudoku aus Abb. 1 mit Farben anstatt Ziffern und 90° Drehung im Uhrzeigersinn
Abbildung 3e. Sudoku aus Abb. 1 mit Farben anstatt Ziffern und horizontal gespiegelt.

Zählt man nur die Sudokus ohne Vertauschung der Ziffern (also z. B. nur die mit der geordneten Zahlenreihe in der ersten Zeile), so ergeben sich 18.383.222.420.692.992 (ca. 18,4 Billiarden) Sudokus. Zählt man nur die Sudokus, die zusätzlich auch unter Drehungen oder Spiegelungen verschieden sind, so verbleiben nur noch 5.472.730.538 (5,5 Milliarden) verschiedene Sudokus (Ed Russell und Frazer Jarvis 2006).[14]

Eindeutige Lösbarkeit

Abbildung 4. Standardsudoku mit nur 17 vorbelegten Feldern

Wenn ein Sudoku-Rätsel nur ein einziges Feld vorgibt, so gibt es offenbar so viele verschiedene Lösungsmöglichkeiten (Vervollständigungen), wie es vollständig ausgefüllte Sudokus gibt, geteilt durch 9. Die in Medien veröffentlichten Sudoku-Rätsel werden mit der Maßgabe erstellt, eindeutig lösbar zu sein:

Ein Sudoku-Rätsel, das nur eine einzige Lösung (Vervollständigung) besitzt, heißt eindeutig lösbar.

Die Eigenschaft, eindeutig lösbar zu sein, sichert hierbei, dass für jede freie Zelle nur eine einzige Ziffer möglich ist. Nicht alle Ziffern müssen in der Vorgabe vorkommen; das Fehlen einer einzigen bedingt nicht eine Mehrdeutigkeit, wohl aber das Fehlen zweier Ziffern.

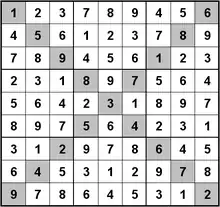
Je weniger Felder in einem Sudoku-Rätsel vorbelegt sind, desto schwieriger ist es in der Regel zu lösen. Abbildung 4 zeigt ein eindeutig lösbares Sudoku mit nur 17 vorbelegten Feldern.[15] Die Vermutung, dass 17 die minimale Anzahl an vorbelegten Feldern ist, für die ein eindeutig lösbares Rätsel existiert,[4][16] bewies 2011 ein Forschungsteam um Gary McGuire (University College Dublin) mit Hilfe von Computern. Die von ihm programmierte erschöpfende Suche benötigte sieben Millionen Stunden Rechenzeit parallel auf Hunderten von Prozessoren.[17][18] Dieses Forschungsergebnis ist allerdings noch nicht in einer Zeitschrift publiziert und wurde noch nicht von anderen Forschern bestätigt. Auch ein mathematischer Beweis (ohne Verwendung eines Computers), der möglicherweise darüber Aufschluss geben könnte, warum die Grenze bei 17 und nicht z. B. bei 16 liegt, steht noch aus.

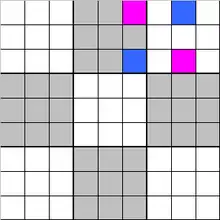
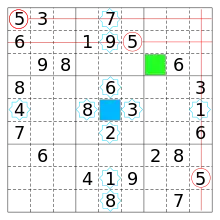
Abbildung 5. Ein vollständig ausgefülltes Sudoku mit zwei Feldern einer Farbe (pink) und zwei Feldern einer anderen Farbe (blau) angeordnet in den Ecken eines Rechtecks

Umgekehrt gibt es Sudoku-Rätsel mit 77 belegten Feldern (also nur vier freien Feldern), die (trotzdem) nicht eindeutig lösbar sind. Wenn beispielsweise in einem (vollständig ausgefüllten) Sudoku wie in Abbildung 5 die pinkfarbenen Felder zu einer Farbe (bzw. einer Ziffer) gehören und die blauen zu einer anderen, dann entsteht durch Vertauschen der Farben Pink und Blau (nur) in diesen vier Feldern ein anderes (vollständig ausgefülltes) Sudoku. Das Sudoku-Rätsel, in dem alle Felder bis auf diese vier vorbelegt sind, ist mithin nicht eindeutig lösbar.[4]

Offensichtlich enthält die Vorbelegung für ein eindeutig lösbares Sudoku-Rätsel mindestens acht verschiedene Farben bzw. Ziffern: Denn verwendet eine Vorbelegung nur (höchstens) sieben Ziffern, so kann man in einer zugehörigen Lösung (einem vollständig ausgefüllten Sudoku) die beiden übrigen Ziffern vertauschen (Herzberg und Murty 2007).[15]

Sudoku: ein Logik- oder ein Enumerationsproblem?

Die in Medien regelmäßig als Rätsel veröffentlichten Sudokus sind fast immer eindeutig lösbar, weil man bis zum Schluss Schritt für Schritt ohne raten zu müssen mit Hilfe logischer Schlussfolgerungen aus bereits belegten Feldern einem freien Feld endgültig eine Ziffer zuweisen kann, so dass schließlich das vervollständigte 9×9-Gitter die Lösung des Sudoku-Rätsels darstellt. Solche ausschließlich logisch zu lösenden Sudoku-Rätsel sind immer eindeutig lösbar.

Bei solchen Sudoku-Rätseln ist es nicht notwendig, (ggf. sogar mehrfach hintereinander) Fallunterscheidungen gemäß dem Prinzip von Versuch und Irrtum vorzunehmen und systematisch die einzelnen Fälle zu überprüfen (Backtracking). Aber die Lösung von Sudokus, die diese Eigenschaften eindeutig lösbar beziehungsweise ausschließlich logisch lösbar nicht tragen, kann schnell sehr aufwendig und mühselig werden. Hier bietet sich der Einsatz automatischer Verfahren wie Graph-Färbungsalgorithmen, Backtracking oder Constraint-Satisfaction-Löser, die Constraint-Propagation-Verfahren nutzen, an.

Folglich ist das verallgemeinerte Sudoku-Problem vermutlich nicht effizient lösbar:

Das verallgemeinerte Sudoku-Problem n-ter Ordnung, n ist eine natürliche Zahl, besteht darin, auf einem N×N-Gitter, N=n², die Zahlen 1 bis N so zu verteilen, dass in jeder Zeile und Spalte sowie in jedem n×n-Block jede der Zahlen 1 bis N genau einmal auftritt, wobei einige der N² Felder vorbelegt sein können.

Das übliche 9×9-Standard-Sudoku hat in diesem Sinne also die Ordnung 3. Die oben genannten Enumerationsverfahren Graph-Färbungsalgorithmen, Backtracking oder Constraint-Satisfaction-Löser können selbstverständlich auch verallgemeinerte Sudoku-Probleme lösen, doch wächst die Anzahl der im schlechtesten Fall benötigten Rechenschritte (die sogenannte Laufzeit dieser Algorithmen) exponentiell mit N. Takayuki Yato und Takahiro Seta von der Universität von Tokyo bewiesen 2002, dass das verallgemeinerte Sudoku-Problem NP-vollständig ist, d. h., dass es keinen polynomiellen Algorithmus für das verallgemeinerte Sudoku-Problem gibt (außer es ist P=NP).[19]

Wettbewerbe

Weltmeisterschaft

Vom 10. bis 12. März 2006 wurden in Lucca (Italien) die ersten offiziellen Sudoku-Weltmeisterschaften durchgeführt. Initiator war der Mailänder Verlag Nonzero, Teilnehmer waren 85 Kandidaten aus 22 Nationen. Weltmeisterin wurde die tschechische Wirtschaftswissenschaftlerin Jana Tylova, den zweiten und dritten Platz belegten mit dem Chemiestudenten Thomas Snyder und dem Softwareentwickler Wei-Hwa Huang zwei US-Amerikaner. Auch vier Deutsche nahmen an der Meisterschaft teil: die drei Siegerinnen und Sieger der deutschen Sudoku-Meisterschaft 2005 sowie Kopfrechnen-Weltmeister Gert Mittring, der von RTL ins Rennen geschickt wurde, aber als Drittletzter sehr schlecht abschnitt.

Die 2. Weltmeisterschaft fand vom 28. März bis zum 1. April 2007 in Prag statt, Weltmeister wurde der Chemiestudent Thomas Snyder. Die deutschen Teilnehmer wurden auf der deutschen Meisterschaft 2006 in Hamburg ermittelt.

Die 3. Weltmeisterschaft fand vom 14. bis 17. April 2008 in Goa (Indien) statt. Im Wettbewerb konnte sich wiederum Thomas Snyder durchsetzen. Die deutsche Mannschaft, bestehend aus Michael Ley, Michael Smid und Kerstin Wöge, belegte im Teamwettbewerb den dritten Platz, hinter der Tschechischen Republik und Japan.

Die 4. Sudoku-Weltmeisterschaft fand vom 24. bis 27. April 2009 in Žilina (Slowakei) statt. Weltmeister wurde Jan Mrozowski (Polen), Teamweltmeister die Slowakei. Bester deutscher Teilnehmer war Michael Ley (Platz 26 bei 128 Teilnehmern), das deutsche Team belegte Platz 9.[20]

Die 5. Sudoku-Weltmeisterschaft fand vom 29. April bis 2. Mai 2010 in Philadelphia (USA) statt. Jan Mrosowski (Polen) verteidigte seinen Titel, Team Deutschland A mit Michael Smit, Michael Ley und Florian Kirch wurde Teamweltmeister. Florian Kirch belegte den 4. Platz in der Einzelwertung.[21]

Die 6. Sudoku-Weltmeisterschaft fand vom 6. bis 19. November 2011 in Eger (Ungarn) statt. Thomas Snyder (USA) holte sich den Titel zurück, Team Deutschland A verteidigte den Team-Titel. Florian Kirch wurde mit Platz 5 bester deutscher Teilnehmer.[22]

Die 7. Sudoku-Weltmeisterschaft fand vom 1. bis 3. Oktober 2012 in Kraljevica (Kroatien) statt. Jan Mrosowski (Polen) eroberte wiederum den Titel, Team Japan A wurde wieder Team-Weltmeister. Michael Ley kam auf Platz 13, das Team Deutschland A auf Platz 4.[23]

Nr.	Datum	Ort	Weltmeister
1	10. bis 12. März 2006	Lucca (Italien)	Jana Tylova (Tschechische Republik)
2	28. März bis 1. April 2007	Prag (Tschechien)	Thomas Snyder (USA)
3	14. bis 17. April 2008	Goa (Indien)	Thomas Snyder (USA)
4	24. bis 27. April 2009	Žilina (Slowakei)	Jan Mrozowski (Polen)[20]
5	29. April bis 2. Mai 2010	Philadelphia (USA)	Jan Mrosowski (Polen)[21]
6	6. bis 19. November 2011	Eger (Ungarn)	Thomas Snyder (USA)[22]
7	1. bis 3. Oktober 2012	Kraljevica (Kroatien)	Jan Mrosowski (Polen)[23]
8	12. bis 14. Oktober 2013	Peking (China)[24]
9	2014	London (Vereinigtes Königreich)	Kota Morinishi (Japan)[25]
10	2015	Sofia (Bulgarien)	Kota Morinishi (Japan)[26]
11	2016	Senec (Slowakei)	Tiit Vunk (Estland)[27]
12	2017	Bengaluru (Indien)	Kota Morinishi (Japan)[28]
13	2018	Prag (Tschechien)
14	2019	Kirchheim (Deutschland)

Deutsche Meisterschaft

2005 wurde von der B.Z. die erste deutsche Sudokumeisterschaft veranstaltet. Erste deutsche Meisterin wurde die Lehramtsstudentin Kerstin Wöge. Der Verein Logic Masters Deutschland e. V., für Deutschland zuständiges Mitglied der World Puzzle Federation, erkannte die Veranstaltung im folgenden Jahr als offizielle deutsche Sudokumeisterschaft an. Er organisierte alle weiteren Meisterschaften.

Literatur

Claudia Bach: Sudoku-Trick-Kiste. Swordfish, X-Wing, Forcing Chains, mehr als 25 wichtige Lösungstechniken für Anfänger und Fortgeschrittene, mit 103 Übungen in 4 Schwierigkeitsstufen. Aegis, Berlin 2006, ISBN 978-3-9811369-1-3.
Richard Bird: Functional pearl: A program to solve Sudoku (Memento vom 2. Dezember 2012 im Internet Archive) (PDF; 95 kB) In: Journal of Functional Programming, Vol. 16. Ein einfacher Sudokulöser in Haskell.
Pia Frey: Die Magie der Zahlen: „Und davon kann man leben?“ In: Der Tagesspiegel Medien, 17. April 2011, S. 31.
Wolfgang Blum: Neun Ziffern gegen einen. In: SZ Wissen, 12/2006, S. 42–51.
Jean-Paul Delahaye: Sudoku oder die einsamen Zahlen. In: Spektrum der Wissenschaft, März 2006, ISSN 0170-2971, S. 100–106.

Weblinks

Wiktionary: Sudoku – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Commons: Sudoku – Sammlung von Bildern, Videos und Audiodateien

Wikibooks: Sudoku – Lern- und Lehrmaterialien

Linkkatalog zum Thema Sudoku-Online bei curlie.org (ehemals DMOZ)
Signum Singulare (Sudokuseite mit ausführlichen Lösungsstrategien)
Deutsche Sudokumeisterschaften
Sudoku-Varianten der ersten Sudokuweltmeisterschaft (PDF, englisch; 2,27 MB)
Sudoku als Thema im Unterricht (im ZUM-Wiki)

Einzelnachweise

Hemme, Heinrich.: Die magischen Vierecke des Abul Wafa : Rätsel und Knobeleien wie aus 1001 Nacht. Orig.-ausg Auflage. Rowohlt-Taschenbuch-Verl, Reinbek bei Hamburg 2004, ISBN 3-499-61969-5.
Howard Garns: Number Place. In: Dell Pencil Puzzles & Word Games. Ausgabe 16, Mai 1979, New York, S. 6.
Ed Pegg Jr., Eric W. Weisstein: Sudoku. Online auf MathWorld (englisch), abgerufen am 11. Dezember 2016.
Jean-Paul Delahaye: The Science behind Sudoku. (PDF; 2,5 MB) In: Scientific American, Juni 2006
Sudoku – History. Online auf Nikoli.co.jp (englisch), abgerufen am 11. Dezember 2016.
Wayne Gould. (Memento vom 20. Februar 2007 im Internet Archive), abgerufen am 11. Dezember 2016.
Beispielhaftes X-Sudoku mit 12 Vorbelegungen.
Christian Boyer: Les ancêtres français du sudoku. (Memento vom 12. Juni 2013 im Internet Archive) (Deutsch: Die französische Ahnengalerie des Sudoku). In: Pour la Science. Nr. 344, Juni 2006, online auf PourLaScience.fr (französisch), abgerufen am 31. Dezember 2016.
Bernd Wehren: Lesen- und Schreibenlernen mit Sudoku. Mildenberger Verlag, Offenburg 2007.
Bernd Wehren: Rechnenlernen mit Sudoku. Brigg Pädagogik Verlag, Augsburg 2013.
Bernd Wehren: Lesen- und Rechtschreibenlernen mit Sudoku. Mildenberger Verlag, Offenburg 2008.
Versteckte Einer. (Memento vom 14. Juli 2014 im Internet Archive) Online auf SignumSingulare.com, abgerufen am 8. Januar 2017.
Bertram Felgenhauer, Frazer Jarvis: Enumerating possible Sudoku grids. (PDF; 91 kB) 20. Juni 2005. Publiziert als: Mathematics of Sudoku I. In: Mathematical Spectrum, 39, 2006, S. 15–22.
Ed Russell, Frazer Jarvis: Mathematics of Sudoku II. Mathematical Spectrum 39, 2006, 54–58.
Agnes M. Herzberg, M. Ram Murty: Sudoku Squares and Chromatic Polynomials (PDF; 229 kB) In: Notices of the AMS, 54 (6), 2007, S. 708–717
Gordon Royle: Minimum Sudoku. Universität von West-Australien
Gary McGuire, Bastian Tugemann, Gilles Civario: There is no 16-Clue Sudoku: Solving the Sudoku Minimum Number of Clues Problem. 2012, arxiv:1201.0749 (englisch).
George Szpiro: Sudokus mit nur einer Lösung: sieben Millionen Computer-Rechenstunden für einen mathematischen Beweis. In: NZZ, 18. Januar 2012
Takayuki Yato, Takahiro Seta: Complexity and Completeness of Finding Another Solution and Its Application to Puzzles (PDF; 256 kB) In: IPSJ SIG Notes 2002, AL-87-2
The 4th World Sudoku Championship Žilina (Slowakia), abgerufen am 27. Mai 2013.
The 5th World Sudoku Championship Philadelphia (USA), abgerufen am 27. Mai 2013.
The 6th World Sudoku Championship Eger (Hungary), abgerufen am 27. Mai 2013.
The 7th World Sudoku Championship Kraljevica (Croatia), abgerufen am 27. Mai 2013.
Information for The 8th World Sudoku Championship Beijing, China (Memento vom 22. Oktober 2013 im Internet Archive), abgerufen am 27. Mai 2013.
Kota Morinishi is First Japanese Sudoku Champion. ibtimes.co.uk
10th WSC, abgerufen am 12. Mai 2018.
WSC 2016, abgerufen am 12. Mai 2018.
WSPC 2017, abgerufen am 12. Mai 2018.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Hemme, Heinrich.: Die magischen Vierecke des Abul Wafa : Rätsel und Knobeleien wie aus 1001 Nacht. Orig.-ausg Auflage. Rowohlt-Taschenbuch-Verl, Reinbek bei Hamburg 2004, ISBN 3-499-61969-5.

[2] Howard Garns: Number Place. In: Dell Pencil Puzzles & Word Games. Ausgabe 16, Mai 1979, New York, S. 6.

[MathWorld-3] Ed Pegg Jr., Eric W. Weisstein: Sudoku. Online auf MathWorld (englisch), abgerufen am 11. Dezember 2016.

[Delahaye2006-4] Jean-Paul Delahaye: The Science behind Sudoku. (PDF; 2,5 MB) In: Scientific American, Juni 2006

[5] Sudoku – History. Online auf Nikoli.co.jp (englisch), abgerufen am 11. Dezember 2016.

[6] Wayne Gould. (Memento vom 20. Februar 2007 im Internet Archive), abgerufen am 11. Dezember 2016.

[7] Beispielhaftes X-Sudoku mit 12 Vorbelegungen.

[8] Christian Boyer: Les ancêtres français du sudoku. (Memento vom 12. Juni 2013 im Internet Archive) (Deutsch: Die französische Ahnengalerie des Sudoku). In: Pour la Science. Nr. 344, Juni 2006, online auf PourLaScience.fr (französisch), abgerufen am 31. Dezember 2016.

[9] Bernd Wehren: Lesen- und Schreibenlernen mit Sudoku. Mildenberger Verlag, Offenburg 2007.

[10] Bernd Wehren: Rechnenlernen mit Sudoku. Brigg Pädagogik Verlag, Augsburg 2013.

[11] Bernd Wehren: Lesen- und Rechtschreibenlernen mit Sudoku. Mildenberger Verlag, Offenburg 2008.

[12] Versteckte Einer. (Memento vom 14. Juli 2014 im Internet Archive) Online auf SignumSingulare.com, abgerufen am 8. Januar 2017.

[13] Bertram Felgenhauer, Frazer Jarvis: Enumerating possible Sudoku grids. (PDF; 91 kB) 20. Juni 2005. Publiziert als: Mathematics of Sudoku I. In: Mathematical Spectrum, 39, 2006, S. 15–22.

[14] Ed Russell, Frazer Jarvis: Mathematics of Sudoku II. Mathematical Spectrum 39, 2006, 54–58.

[HerzbergMurty2007-15] Agnes M. Herzberg, M. Ram Murty: Sudoku Squares and Chromatic Polynomials (PDF; 229 kB) In: Notices of the AMS, 54 (6), 2007, S. 708–717

[16] Gordon Royle: Minimum Sudoku. Universität von West-Australien

[17] Gary McGuire, Bastian Tugemann, Gilles Civario: There is no 16-Clue Sudoku: Solving the Sudoku Minimum Number of Clues Problem. 2012, arxiv:1201.0749 (englisch).

[18] George Szpiro: Sudokus mit nur einer Lösung: sieben Millionen Computer-Rechenstunden für einen mathematischen Beweis. In: NZZ, 18. Januar 2012

[19] Takayuki Yato, Takahiro Seta: Complexity and Completeness of Finding Another Solution and Its Application to Puzzles (PDF; 256 kB) In: IPSJ SIG Notes 2002, AL-87-2

[SudokuWm2009-20] The 4th World Sudoku Championship Žilina (Slowakia), abgerufen am 27. Mai 2013.

[SudokuWm2010-21] The 5th World Sudoku Championship Philadelphia (USA), abgerufen am 27. Mai 2013.

[SudokuWm2011-22] The 6th World Sudoku Championship Eger (Hungary), abgerufen am 27. Mai 2013.

[SudokuWm2012-23] The 7th World Sudoku Championship Kraljevica (Croatia), abgerufen am 27. Mai 2013.

[SudokuWm2013-24] Information for The 8th World Sudoku Championship Beijing, China (Memento vom 22. Oktober 2013 im Internet Archive), abgerufen am 27. Mai 2013.

[25] Kota Morinishi is First Japanese Sudoku Champion. ibtimes.co.uk

[26] 10th WSC, abgerufen am 12. Mai 2018.

[27] WSC 2016, abgerufen am 12. Mai 2018.

[28] WSPC 2017, abgerufen am 12. Mai 2018.