Standzeit (Zerspanen)

Die Standzeit ist beim Zerspanen eine wichtige Standgröße, die die Zeit angibt, die ein Zerspanungswerkzeug tatsächlich genutzt werden kann, bis es nachgeschliffen oder ausgetauscht werden muss. Es wird dabei nur die Zeit gemessen, während der das Werkzeug wirklich Zerspanarbeit leistet. Werkstückwechselzeiten und sonstige Zeiten, während denen die Werkzeuge nicht genutzt werden, zählen nicht zur Standzeit. In der modernen industriellen Fertigung liegen typische Standzeiten bei 15 bis 30 Minuten. Weitere Standgrößen sind Standmenge, -weg und -volumen. Sie gelten dabei nur für bestimmte Standbedingungen. Die wichtigsten sind der zu bearbeitende Werkstoff, das Material des Werkzeuges (sogenannter Schneidstoff) und die Schnittgeschwindigkeit. Die Standzeit ist ein Kriterium, um die Zerspanbarkeit von Werkstoffen zu beurteilen. Grundsätzlich verringern steigende Schnittgeschwindigkeiten die Standzeit, Bearbeitungszeit und anteilige Maschinen- und Lohnkosten. Dafür steigen jedoch die Werkzeugkosten und die Anzahl der nötigen Werkzeugwechsel. Frederick Winslow Taylor fand mit der nach ihm benannten Taylor-Geraden einen vereinfachten mathematischen Zusammenhang zwischen der Standzeit $T$ und der Schnittgeschwindigkeit $v_{c}$ in der Form $T=c_{v}\cdot v_{c}^{k}$ mit den Konstanten $c_{v}$ und $k$ . Mit ihm ist es möglich, optimale Standzeiten und Schnittgeschwindigkeiten zu finden, die entweder zu minimalen Stückkosten oder minimalen Bearbeitungszeiten führen.[1]

Typische Werte der Standzeit

Bei CNC-Maschinen, die typischerweise kleine Rüstzeiten haben, liegen die Standzeiten bei 15 bis 30 Minuten. Bei Maschinen mit mittlerer Rüstzeit dagegen liegen sie bei etwa 60 Minuten. Dazu zählen etwa Revolverdrehautomaten. Bei Maschinen mit langen Rüstzeiten wie kurvengesteuerten Drehautomaten oder Transferstraßen liegt sie bei 240 Minuten (4 Stunden).[2]

Der Standzeit und den verschiedenen anderen Standgrößen sind immer zugehörige Standkriterien und Standbedingungen zugeordnet. $T_{VB0,2;vc200}=60\ min$ beispielsweise bedeutet, dass die Standzeit $T$ bis zum Erreichen einer Verschleißmarkenbreite $VB$ von 0,2 mm bei einer Schnittgeschwindigkeit $v_{c}$ von 200 m/min gleich 60 Minuten ist.[1]

Einflüsse

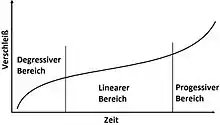
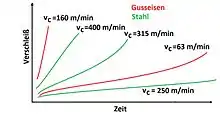
Schematischer Verlauf des Verschleißes beim Spanen über die Zeit

Einflüsse von Schnittgeschwindigkeit und Werkstoff auf die Standzeit

Einflüsse auf die Standzeit

Es lassen sich zwei Gruppen von Größen unterscheiden, die Einfluss auf die Standzeit haben: solche, die sich während der Bearbeitung nicht mehr verändern lassen, und solche, die sich verändern lassen. Zur ersten Gruppe zählen der Schneidstoff, der Werkstoff, die Werkzeuggeometrie, der Kühlschmierstoff sowie das dynamische Verhalten von Werkzeug, Werkstück und Werkzeugmaschine. Einstellbar sind dagegen die Schnittgeschwindigkeit, der Vorschub und die Schnitttiefe.[3]

Der zeitliche Verlauf der Verschleißgrößen wird häufig experimentell ermittelt und in Verschleiß-Standzeit-Kurven dargestellt. Dabei lässt sich ein zu Beginn stark steigender Verschleiß feststellen, der jedoch mit der Zeit langsamer steigt (degressiver Verschleiß). Danach gibt es einen längeren Bereich, in dem der Verschleiß annähernd proportional zur Zeit ist (linearer Bereich), um schließlich immer stärker anzuwachsen (progressiver Bereich). Dieser Versuch wird insbesondere für harte Schneidstoffe wie Hartmetall, Schneidkeramik und Bornitrid durchgeführt. Das sind diejenigen Schneidstoffe, bei denen nicht die Temperatur zum Erliegen des Werkzeuges führt, sondern ein zunehmender Verschleiß.[4]

Der Temperatur-Standzeit-Versuch wird dagegen durchgeführt, wenn die thermische Belastung zum Erweichen des Werkzeuges führt, was bei Werkzeugstählen ab 300 °C und Schnellarbeitsstahl ab 600 °C der Fall ist. Bei diesen Temperaturen erweichen die Schneiden und führen zur sogenannten Blankbremsung.[5]

Einflüsse der Standzeit auf andere Größen

Bei steigender Standzeit verringern sich die Werkzeugkosten und die Werkzeug-Wechselkosten, da weniger Werkzeuge verbraucht werden und daher auch seltener gewechselt werden müssen. Bei vorgegebenen Werkzeugen sind höhere Standzeiten jedoch auch mit niedrigeren Schnittgeschwindigkeiten und somit höheren Bearbeitungszeiten verbunden. Vor allem die Hauptzeit steigt. Damit verbunden steigen auch die anteiligen Lohn- und Maschinenkosten.[6]

Standzeitberechnung

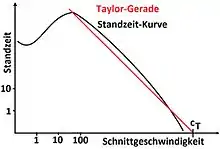
Taylor-Gerade (rot) und reale Standzeit-Kurve (schwarz)

Frederick Winslow Taylor fand gegen 1900 heraus, dass bei gegebenen Werkstück-Werkstoff-Paarungen und gegebenen Werkzeugen die Schnittgeschwindigkeit den größten Einfluss auf die Standzeit hat. Trägt man aus den Standzeit-Schnittgeschwindigkeits-Versuchen die Werte in ein doppelt-logarithmisches Diagramm ein, so ergibt sich in einem weiten Bereich ein annähernd linearer Verlauf, welcher durch die Taylor-Gerade angenähert wird. Sie hat die Form[7]

v_{c}\cdot T^{-{\frac {1}{k}}}=c_{T}

oder

T=c_{v}\cdot v_{c}^{k}

.

Mit:

v_{c}

- Schnittgeschwindigkeit

k

- Konstante die die Steigung der Geraden angibt

c_{v}

- theoretische Standzeit bei einer Schnittgeschwindigkeit von einem Meter pro Minute

c_{T}

-theoretische Schnittgeschwindigkeit für eine Standzeit von einer Minute.

Im doppelt logarithmischen System gilt der Zusammenhang

\log T=k\cdot \log v_{c}+\log c_{v}.

Zwischen den Konstanten besteht folgender Zusammenhang:

c_{v}={\frac {1}{c_{T}^{k}}}

Die Konstanten können aus Tabellen abgelesen oder experimentell ermittelt werden. Je steiler die Gerade einer bestimmten Werkstoff-Schneidstoff-Kombination ist, desto empfindlicher reagiert die Standzeit auf Veränderungen der Schnittgeschwindigkeit. Wenn für ein Werkzeug mehrere Geraden für verschiedene Werkstoffe vorliegen, so sind diese nach links und rechts gegeneinander verschoben. Bei harten, besonders verschleißbeständigen Schneidstoffen verläuft sie flacher.[8] Die Gerade für Freiflächenverschleiß als Standkriterium verläuft flacher als diejenige für Kolkverschleiß. Wenn beide Verschleißerscheinungen auftreten, so dominiert bei niedrigen Schnittgeschwindigkeiten meist der Freiflächenverschleiß und bei hohen der Kolkverschleiß.[9]

Die Taylor-Gerade bietet jedoch nur innerhalb gewisser Grenzen ausreichend genaue Ergebnisse.[10] Bei geringen Schnittgeschwindigkeiten weicht sie von der realen Kurve wegen der Aufbauschneidenbildung ab, bei großen wegen des steigenden Verschleißes. Es ist für die Praxis daher nötig, diese Grenzen zu kennen, um keine unrealistischen Werte zu erhalten. Von Vorteil ist dagegen ihre einfache mathematische Handhabung. Außerdem lassen sie sich in der Praxis sehr leicht experimentell ermitteln, da nur zwei Punkte der Geraden bekannt sein müssen.[7]

Nachdem von Taylor die grundsätzlichen Zusammenhänge entdeckt waren, wurden sie durch weitere Arbeiten von Max Kronenberg der praktischen Anwendung zugänglich gemacht. Er zeigte auch, dass die Anwendung der Ähnlichkeitsmechanik zu denselben Ergebnissen führt.[11]

Die Taylor-Gerade wird auch als einfache Standzeitfunktion bezeichnet, da sie nur die Schnittgeschwindigkeit als Variable enthält. Die erweiterte Form berücksichtigt auch den Einfluss des Vorschubes $f$ und der Schnitttiefe $a_{p}$ :[11]

T=C\cdot v_{c}^{k}\cdot f_{z}^{k_{fz}}\cdot a_{p}^{k_{a}}

mit $f_{z}$ als Zahnvorschub (Vorschub pro Zahn) und den Konstanten $k_{fz}$ und $k_{a}$ . Eine etwas andere Darstellung[8] ist

T=c_{v}\cdot v_{c}^{k}\cdot c_{f}\cdot f_{z}^{k_{fz}}\cdot c_{a}\cdot a_{p}^{k_{a}}

In der industriellen Praxis werden bei der Optimierung der Schnittwerte jedoch zuerst die Schnitttiefe und anschließend der Vorschub ausgewählt, sodass diese bereits feststehen, was die Verwendung der einfachen Gleichung erlaubt.

Optimierung

Da eine höhere Standzeit bzw. eine niedrigere Schnittgeschwindigkeit auf manche Kosten einen positiven Einfluss hat und auf andere einen negativen, ergibt sich eine u-förmige Gesamtkostenkurve in Abhängigkeit von der Standzeit bzw. Schnittgeschwindigkeit. Daher lassen sich mit der Taylor-Geraden auch optimale Werte für die Gesamtkosten ermitteln. Es wird zwischen mehreren Zielsetzungen unterschieden:

Minimieren der Fertigungskosten
Minimieren der Fertigungszeit

Unter normalen Umständen werden die Kosten optimiert. Dafür müssen jedoch die Werkzeug-, Lohn- und Maschinenkosten bekannt sein. Falls es zu Produktionsengpässen kommt, ist die kürzeste Fertigungszeit gesucht. Sie setzt sich zusammen aus der Hauptzeit $t_{H}$ , während derer das Werkzeug Arbeit verrichtet, und der Werkzeugwechselzeit $t_{W}$ , die zum Wechseln der verschlissenen Werkzeuge dient.[12]

Die Fertigungskosten ergeben sich zu

K_{F}=K_{ML}\cdot t_{H}+{\frac {t_{H}}{T}}\cdot (K_{ML}\cdot t_{W}+K_{WT})

.

Dabei ist $K_{ML}$ der Maschinen- und Lohnkostensatz, also die Kosten von Personal und Maschinen je Stunde, und $K_{WT}$ die Werkzeugkosten je Standzeit. Das Minimum ist dann an der Stelle

T_{ok}=-(k+1)\left(t_{W}+{\frac {K_{WT}}{K_{ML}}}\right)

.

Durch den gleichen Ansatz ergibt sich die zeitoptimale Standzeit zu

T_{ot}=-(k+1)\cdot t_{W}

.

Die zeitoptimale Standzeit ist grundsätzlich mit höheren Kosten verbunden als bei der kostenoptimalen Standzeit. Es lassen sich also nicht beide Ziele gleichzeitig erreichen.[13]

Standzeitstreuung

Die tatsächlichen Standzeiten unterliegen einer gewissen Streuung. Diese ergibt sich selbst dann, wenn die Prozessparameter exakt eingehalten werden. Die Streuung lässt sich zurückführen auf geometrische Abweichungen der Rohteile und chemische oder physikalische Abweichungen der Eigenschaften von Werkstoff oder Schneidstoff.[14]

Siehe auch

Literatur

Alfred Herbert Fritz, Günter Schulze (Hrsg.): Fertigungstechnik. 11. Auflage. Springer Vieweg, Berlin/Heidelberg 2015, ISBN 9783662465554.
Berend Denkena, Hans Kurt Tönshoff: Spanen – Grundlagen. 3. Auflage. Springer, Berlin/Heidelberg 2011, ISBN 978-3-642-19771-0.
Fritz Klocke, Wilfried König: Fertigungsverfahren 1 – Drehen, Fräsen, Bohren. 8. Auflage. Springer, 2008, ISBN 3-540-23458-6.
Herbert Schönherr: Spanende Fertigung. Oldenbourg, München/Wien 2002, ISBN 3-486-25045-0.
Heinz Tschätsch: Praxis der Zerspantechnik. 7. Auflage. Vieweg.

Einzelnachweise

Alfred Herbert Fritz, Günter Schulze: Fertigungstechnik. 11. Auflage. Springer, 2015, S. 289 f.
Heinz Tschätsch: Praxis der Zerspantechnik. 7. Auflage. Vieweg, S. 27.
Berend Denkena, Hans Kurt Tönshoff: Spanen – Grundlagen. 3. Auflage. Springer, 2011, S. 149.
Fritz Klocke, Wilfried König: Fertigungsverfahren 1. 8. Auflage. Springer, 2008, S. 263.
Fritz Klocke, Wilfried König: Fertigungsverfahren 1. 8. Auflage. Springer, 2008, S. 262 f.
Herbert Schönherr: Spanende Fertigung. Oldenbourg, 2002, S. 50 f.
Alfred Herbert Fritz, Günter Schulze: Fertigungstechnik. 11. Auflage. Springer, 2015, S. 307.
Fritz Klocke, Wilfried König: Fertigungsverfahren 1 – Drehen, Fräsen, Bohren. 8. Auflage. Springer, 2008, S. 379.
Berend Denkena, Hans Kurt Tönshoff: Spanen – Grundlagen. 3. Auflage. Springer, 2011, S. 149–152.
Alfred Herbert Fritz, Günter Schulze: Fertigungstechnik. 11. Auflage. Springer 2015, S. 306.
Fritz Klocke, Wilfried König: Fertigungsverfahren 1 – Drehen, Fräsen, Bohren. 8. Auflage. Springer, 2008, S. 265.
Alfred Herbert Fritz, Günter Schulze: Fertigungstechnik. 11. Auflage. Springer, 2015, S. 307 f.
Alfred Herbert Fritz, Günter Schulze: Fertigungstechnik. 11. Auflage. Springer, 2015, S. 309.
Berend Denkena, Hans Kurt Tönshoff: Spanen – Grundlagen. 3. Auflage. Springer, 2011, S. 153–156.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Fritz/Schulze_289-1] Alfred Herbert Fritz, Günter Schulze: Fertigungstechnik. 11. Auflage. Springer, 2015, S. 289 f.

[2] Heinz Tschätsch: Praxis der Zerspantechnik. 7. Auflage. Vieweg, S. 27.

[3] Berend Denkena, Hans Kurt Tönshoff: Spanen – Grundlagen. 3. Auflage. Springer, 2011, S. 149.

[4] Fritz Klocke, Wilfried König: Fertigungsverfahren 1. 8. Auflage. Springer, 2008, S. 263.

[5] Fritz Klocke, Wilfried König: Fertigungsverfahren 1. 8. Auflage. Springer, 2008, S. 262 f.

[6] Herbert Schönherr: Spanende Fertigung. Oldenbourg, 2002, S. 50 f.

[Alfred_Herbert_Fritz_2015-7] Alfred Herbert Fritz, Günter Schulze: Fertigungstechnik. 11. Auflage. Springer, 2015, S. 307.

[DFB-8] Fritz Klocke, Wilfried König: Fertigungsverfahren 1 – Drehen, Fräsen, Bohren. 8. Auflage. Springer, 2008, S. 379.

[9] Berend Denkena, Hans Kurt Tönshoff: Spanen – Grundlagen. 3. Auflage. Springer, 2011, S. 149–152.

[10] Alfred Herbert Fritz, Günter Schulze: Fertigungstechnik. 11. Auflage. Springer 2015, S. 306.

[Fritz-11] Fritz Klocke, Wilfried König: Fertigungsverfahren 1 – Drehen, Fräsen, Bohren. 8. Auflage. Springer, 2008, S. 265.

[12] Alfred Herbert Fritz, Günter Schulze: Fertigungstechnik. 11. Auflage. Springer, 2015, S. 307 f.

[13] Alfred Herbert Fritz, Günter Schulze: Fertigungstechnik. 11. Auflage. Springer, 2015, S. 309.

[14] Berend Denkena, Hans Kurt Tönshoff: Spanen – Grundlagen. 3. Auflage. Springer, 2011, S. 153–156.