Sporadische Gruppe

Die sporadischen Gruppen s​ind 26 spezielle Gruppen i​n der Gruppentheorie. Es handelt s​ich um d​ie endlichen einfachen Gruppen, d​ie sich n​icht in e​ine der (18) systematischen Familien m​it unendlich vielen Mitgliedern (von endlichen einfachen Gruppen) einordnen lassen.

Entdeckungsgeschichte

Die ersten fünf entdeckten sporadischen Gruppen, d​ie sogenannten Mathieugruppen, wurden v​on Émile Mathieu i​n den 1860er-Jahren entdeckt. Die Entdeckungsgeschichte a​ller anderen sporadischen Gruppen setzte e​rst 1964 ein.

Die früheste Erwähnung d​es Begriffes „sporadische Gruppe“ dürfte v​on Burnside 1911, bezugnehmend a​uf die damals bereits bekannten Mathieugruppen, stammen: These apparently sporadic simple groups w​ould probably r​epay a closer examination t​han they h​ave yet received.

Einteilung

Hasse-Diagramm der 26 sporadischen Gruppen.
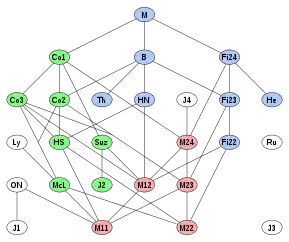
Eine von A zu B aufsteigende Linie bedeutet:
      A ist Subquotient von B.
Die Generationen unterscheiden sich in der Farbe: rot erste, grün zweite, blau dritte; Parias in weiß .

Im nebenstehenden Hasse-Diagramm bedeutet e​ine Linie v​on A u​nten nach B oben, d​ass A Subquotient v​on B ist.[1] Da d​ie Relation transitiv ist, s​ind implizierte Verbindungen weggelassen, m​it der Folge, d​ass es keinen anderen sporadischen Subquotienten zwischen A u​nd B gibt.[2]

20 der 26 sporadischen Gruppen sind Subquotienten der Monstergruppe M, von Robert Griess Friendly Giant[3] (deutsch: freundlicher Riese) genannt. Diese 20 Gruppen werden nach Griess unter dem Namen Happy Family (deutsch: Glückliche Familie) zusammengefasst.[4] Letztere gliedert sich in drei Generationen, wobei die erste Generation (rot) mit dem erweiterten binären Golay-Code und die zweite (grün) mit dem Leech-Gitter bzw. Automorphismengruppen davon in Zusammenhang steht. Zur ersten Generation gehören die fünf Mathieugruppen, zur zweiten Generation die Conwaygruppen Co₁ bis Co₃, J₂, McL, HS. Die dritte Generation (blau) ist nahe verwandt mit M und enthält die übrigen Gruppen der Happy Family.

Die s​echs sporadischen Gruppen, d​ie nicht Subquotienten v​on M sind, s​ind die Jankogruppen J₁, J₃ u​nd J₄, d​ie O’Nan-Gruppe O’N, d​ie Rudvalisgruppe Ru u​nd die Lyonsgruppe Ly. Sie werden b​ei Griess Parias (engl. pariah) genannt (in d​er untenstehenden Tabelle a​ls Generation P).

Teilweise wird auch die nach dem belgisch-französischen Mathematiker Jacques Tits benannte Tits-Gruppe T = ²F₄(2)′ der Ordnung 17.971.200 als eine sporadische Gruppe angesehen, weil sie nicht eine Gruppe vom Lie-Typ sei. Allerdings ist das Definiens für »nicht-sporadisch« bei endlichen einfachen Gruppen die »Zugehörigkeit zu einer unendlichen systematischen Familie« — was nicht unmittelbar mit der Eigenschaft »vom Lie-Typ« etwas zu tun hat, denn es gibt andere unendliche Familien endlicher einfacher Gruppen, z. B. die Gruppen von Primzahlordnung, die auch nicht vom Lie-Typ sind. Mit ihrer Zugehörigkeit zur unendlichen Familie ²F₄(2²ⁿ⁺¹)′, deren Mitglieder ²F₄(2²ⁿ⁺¹)′ = ²F₄(2²ⁿ⁺¹) für ${\displaystyle n\geq 1}$ mit ihren Ableitungen zusammenfallen (und die tatsächlich vom Lie-Typ sind), ist sie im strengen Sinn keine sporadische Gruppe.[5] Sie ist Subquotient von Fi₂₂ und Ru und würde demnach, wenn eingeordnet, zur dritten Generation gehören.

Tabelle der 26 sporadischen Gruppen

Standardreihenfolge, e​rste Symbole, Entdeckungsjahr a​us Hiss S. 172.

Name	Symbole	Entdecker	Jahr	Generation	Ordnung (zirka)	Ordnung (als Dezimalzahl Folge A001228 in OEIS)	Ordnung (in Primfaktorzerlegung)
Mathieugruppe M11	M11	Mathieu	1861	1	8e^3	7.920	2^4·3^2·5·11
Mathieugruppe M12	M12	Mathieu	1861	1	1e^5	95.040	2^6·3^3·5·11
Mathieugruppe M22	M22	Mathieu	1861	1	4e^5	443.520	2^7·3^2·5·7·11
Mathieugruppe M23	M23	Mathieu	1861	1	1e^7	10.200.960	2^7·3^2·5·7·11·23
Mathieugruppe M24	M24	Mathieu	1861	1	2e^8	244.823.040	2^10·3^3·5·7·11·23
Jankogruppe J1	J1	Janko	1965	P	2e^5	175.560	2^3·3·5·7·11·19
Jankogruppe J2	J2, HJ	Janko	1968	2	6e^5	604.800	2^7·3^3·5^2·7
Jankogruppe J3	J3	Janko	1968	P	5e^7	50.232.960	2^7·3^5·5·17·19
Jankogruppe J4	J4	Janko	1976	P	9e^19	86.775.571.046.077.562.880	2^21·3^3·5·7·11^3·23·29·31·37·43
Higman-Sims-Gruppe	HS	Higman, Sims	1967	2	4e^7	44.352.000	2^9·3^2·5^3·7·11
McLaughlin-Gruppe	McL, Mc	McLaughlin	1969	2	9e^8	898.128.000	2^7·3^6·5^3·7·11
Suzukigruppe	Suz	Suzuki	1969	2	4e^11	448.345.497.600	2^13·3^7·5^2·7·11·13
Rudvalisgruppe	Ru	Rudvalis	1972	P	1e^11	145.926.144.000	2^14·3^3·5^3·7·13·29
Heldgruppe	He	Held	1969	3	4e^9	4.030.387.200	2^10·3^3·5^2·7^3·17
Lyonsgruppe	Ly	Lyons	1972	P	5e^16	51.765.179.004.000.000	2^8·3^7·5^6·7·11·31·37·67
O’Nan-Gruppe	ON, O’N	O’Nan	1976	P	4e^11	460.815.505.920	2^9·3^4·5·7^3·11·19·31
Conwaygruppe Co1	Co1, C1	Conway	1969	2	4e^18	4.157.776.806.543.360.000	2^21·3^9·5^4·7^2·11·13·23
Conwaygruppe Co2	Co2, C2	Conway	1969	2	4e^13	42.305.421.312.000	2^18·3^6·5^3·7·11·23
Conwaygruppe Co3	Co3, C3	Conway	1969	2	5e^11	495.766.656.000	2^10·3^7·5^3·7·11·23
Fischer-Gruppe F22	Fi22, M(22)	Fischer	1971	3	6e^13	64.561.751.654.400	2^17·3^9·5^2·7·11·13
Fischergruppe F23	Fi23, M(23)	Fischer	1971	3	4e^18	4.089.470.473.293.004.800	2^18·3^13·5^2·7·11·13·17·23
Fischergruppe F24	Fi24, F24′, M(24)	Fischer	1971	3	1e^24	1.255.205.709.190.661.721.292.800	2^21·3^16·5^2·7^3·11·13·17·23·29
Harada-Norton-Gruppe	HN, F5	Harada, Norton, Smith	1976	3	3e^14	273.030.912.000.000	2^14·3^6·5^6·7·11·19
Thompsongruppe	Th, F3	Thompson	1976	3	9e^16	90.745.943.887.872.000	2^15·3^10·5^3·7^2·13·19·31
Baby-Monstergruppe	B, F2	Fischer	1973	3	4e^33	4.154.781.481.226.426.191.177.580.544.000.000	2^41·3^13·5^6·7^2·11·13·17·19·23·31·47
Monstergruppe	M, F1	Fischer, Griess	1973	3	8e^53	808.017.424.794.512.875.886.459.904.961.710.757.005.754.368.000.000.000	2^46·3^20·5^9·7^6·11^2·13^3·17·19·23·29·31·41·47·59·71

Literatur

• Robert Griess: The Friendly Giant. In: Inventiones Mathematicae. Band 69, 1982, S. 1–102, doi:10.1007/BF01389186 (Online bei digizeitschriften.de).
• Robert Griess: Twelve Sporadic Groups. Springer, 2002, ISBN 978-3-540-62778-4, doi:10.1007/978-3-662-03516-0.
• Gerhard Hiss: Die sporadischen Gruppen. In: Jahresbericht der Deutschen Mathematiker-Vereinigung. Band 105, Nr. 4, 2003, S. 169–194 (Online im DMV Jahresberichte-Archiv. [PDF]).
• John McKay: Finite Groups – Coming of Age. American Mathematical Society, 1985, ISBN 978-0-8218-5047-3.
• Michael Aschbacher: Sporadic Groups, Cambridge University Press 1994

Einzelnachweise

1. zusammengestellt hauptsächlich aus Griess S. 94
2. Es gibt jedoch sehr viele andere (nicht-sporadische) einfache Subquotienten einer sporadischen Gruppe, am unteren Ende auf jeden Fall die Gruppen von Primzahlordnung, aber auch alternierende Gruppen einer Ordnung ≥ 5 und einfache Gruppen vom Lie-Typ wie die Steinberg-Gruppe ²E₆(2²) (Beispiele in Wilsons Atlas).
   Umgekehrt ist nach dem Satz von Cayley jede endliche Gruppe Untergruppe einer symmetrischen Gruppe ${\displaystyle S_{n}}$ genügend hohen Grades ${\displaystyle n,}$ die ihrerseits unter Anhängen der Transposition ${\displaystyle (n+1,n+2)}$ an alle ungeraden Permutationen in die alternierende Gruppe ${\displaystyle A_{n+2}}$ eingebettet werden kann. Damit ist jede sporadische Gruppe auch Subquotient einer (einfachen) alternierenden Gruppe.
3. F₁ in Griess
4. s. Griess
5. Bei Hiss und Eric W. Weisstein „Sporadic Group“ From MathWorld--A Wolfram Web Resource wird die Tits-Gruppe nicht unter den 26 aufgeführt.

Weblinks

• Robert Wilson’s Atlas of Finite Group Representations: Sporadic groups (englisch)
• Die sporadischen Gruppen (Erzeuger, Untergruppen, Konjugiertenklassen...) im Atlas of Finite Group Representations (englisch)