Schuler-Periode

Die Schuler-Periode ist eine geodätische Konstante, die bei der Anwendung der Kreiseltheorie[1][2] auf Navigationsprobleme von großer Bedeutung ist. Die Periode ist gleich der Schwingungsdauer eines hypothetischen Pendels mit einer dem Erdradius R_E entsprechenden Pendellänge (6371 km) in einem homogenen Gravitationsfeld mit der an der Erdoberfläche herrschenden Fallbeschleunigung (g = 9,81 m/s²). Die Untersuchungen dazu gehen zurück auf Maximilian Schuler.

T=2\pi {\sqrt {\frac {R_{E}}{g}}}=84,4

Minuten (Schuler-Periode)

Anmerkungen

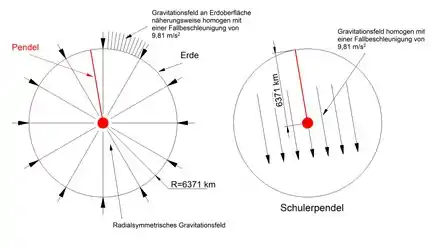
Verhältnisse beim hypothetischen Schulerpendel

Ein solches Pendel (vgl. Bild) ist in jeder Hinsicht hypothetisch. Weder kann seine Größe realisiert, noch kann es durch die Erde zu deren Mittelpunkt geführt werden. Ferner liegt um den Erdmittelpunkt ein Radialfeld und kein homogenes Feld vor (an der Erdoberfläche kann das Radialfeld näherungsweise als homogen angesehen werden).

Dieses hypothetische Pendel ist nicht zu verwechseln mit dem Schuler-Pendel, das für hochpräzise Pendeluhren von M. Schuler entwickelt wurde [3].

Erläuterung

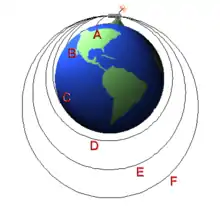
Ein grundlegendes Problem bei der Navigation eines Fahrzeuges auf bzw. über der Erdoberfläche ist die Feststellung der Lotrichtung (Richtung zum Erdmittelpunkt) bzw. der dazu senkrechten Ebene (Künstlicher Horizont). Für ein ruhendes oder sich mit gleichmäßiger Geschwindigkeit bewegendes Fahrzeug kann dies in einfacher Weise mit einem Kugelpendel (nach allen Richtungen auslenkbar) beliebiger Länge geschehen. Es zeigt immer zum Mittelpunkt der (sich drehenden) Erde (vgl. Bild).

Unterliegt das Fahrzeug jedoch einer Beschleunigung (Änderung der Geschwindigkeit), wird das Pendel ausgelenkt und es kommt zu einer Missweisung. Z. B.. wird beim Anfahren des Fahrzeuges der Pendelkörper gegenüber dem sich mit dem Fahrzeug bewegenden Aufhängepunkt des Pendels entgegen der Fahrtrichtung zurückbleiben und bei Erreichen einer konstanten Geschwindigkeit (abklingend) hin und her schwingen.

Max Schuler hat in seiner Veröffentlichung von 1923[4] untersucht, welche Bedingung ein Pendel erfüllen muss, damit es auch bei Beschleunigung seines Aufhängepunktes die Lotrichtung anzeigt. Es ergab sich die Schuler-Periode für die Schwingungsdauer. Da ein Pendel mit dieser Periode nicht realisierbar ist, sind stattdessen Systeme erforderlich, mit denen eine solche extrem lange Schwingungsdauer (und somit die Beschleunigungsunempfindlichkeit) erreichbar ist. Das sind Kreiselgeräte, die sich mit den zu navigierenden Fahrzeugen auf oder nahe der Erdoberfläche im dort herrschenden (näherungsweise homogenen) Gravitationsfeld bewegen. Die Schuler-Periode hat deshalb weitreichende Bedeutung insbesondere für die Theorie der für Navigationszwecke verwendeten (schwingungsfähigen) Kreiselgeräte.

Herleitung der Bedingung nach Schuler

Ruhendes Fahrzeug auf der Erdoberfläche

Bewegung eines Fahrzeuges auf der Erdoberfläche

Beschleunigung eines Fahrzeuges auf der Erdoberfläche

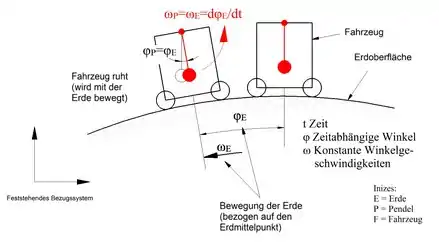
Ein Kugelpendel in einem auf der Erdoberfläche ruhenden oder sich mit gleichmäßiger Geschwindigkeit bewegenden Fahrzeug zeigt immer zum Erdmittelpunkt. Beim ruhenden Fahrzeug verdreht sich das Pendel in einer bestimmten Zeit um einen Winkel, der dem Verdrehungswinkel der Erde in der gleichen Zeit entspricht. Erde und Pendel drehen sich also mit der gleichen Winkelgeschwindigkeit, wobei das Pendel relativ zum Fahrzeug ruht (also nicht pendelt, sondern stets zum Erdmittelpunkt zeigt). Das Bezugsystem, auf das sowohl die Erddrehung als auch die Pendeldrehung bezogen werden (also die Winkelangaben) dreht sich nicht mit der Erde mit. Nach einer Erdumdrehung hat sich das Pendel also einmal gedreht, während es relativ zum Fahrzeug vollkommen in Ruhe bleibt.

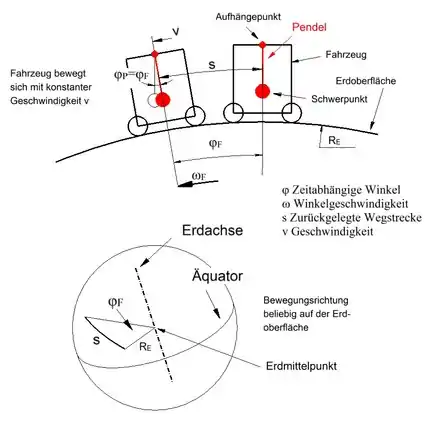
Ein Fahrzeug kann sich selbstverständlich in beliebiger Richtung bewegen. Bei konstanter Geschwindigkeit addieren sich die (konstanten) Winkelgeschwindigkeiten von Erde und Fahrzeug vektoriell, wobei das Pendel wiederum relativ zum Fahrzeug ruht.

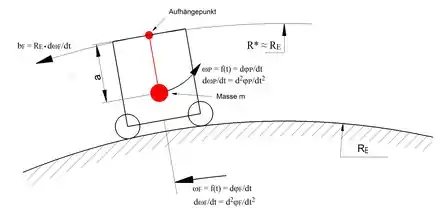
Die Erddrehung braucht bei der Untersuchung von Beschleunigungseffekten nicht berücksichtigt zu werden. Bei Beschleunigung des Fahrzeugs (Änderung der Winkelgeschwindigkeit ω_F) wird der Aufhängepunkt des Pendels in gleicher Weise beschleunigt und dem Pendel wird eine Winkelgeschwindigkeit ω_P in Beschleunigungsrichtung erteilt, wobei es sich zwangsläufig auf einer Kreisbahn um seinen Aufhängepunkt bewegt. Das Pendel ruht vor der Beschleunigung und zeigt also, wie oben erwähnt, zum Erdmittelpunkt. Das Fahrzeug und damit der Aufhängepunkt bewegen sich auf einer Kreisbahn um den Erdmittelpunkt (in beliebiger Richtung), so dass für die Beschleunigung b_F gilt (siehe Bild):

b_{\text{F}}=R_{\text{E}}{\frac {\mathrm {d} \omega _{\text{F}}}{\mathrm {d} t}}

Auf die Masse m des (mathematischen) Pendels wirkt das Drehmoment

M=b_{\text{F}}ma

,

wobei ɑ die Pendellänge ist. Dieses Drehmoment verursacht eine Änderung der Winkelgeschwindigkeit des Pendels (Trägheitsmoment : $\theta =ma^{2}$ ):

ma^{2}{\frac {\mathrm {d} \omega _{\text{P}}}{\mathrm {d} t}}=b_{\text{F}}ma

also

ma^{2}{\frac {\mathrm {d} \omega _{\text{P}}}{\mathrm {d} t}}=maR_{\text{E}}{\frac {\mathrm {d} \omega _{\text{F}}}{\mathrm {d} t}}

Wenn das Pendel bei Beschleunigung unverändert zum Erdmittelpunkt zeigen soll, müssen die durch die Beschleunigung hervorgerufenen Änderungen der (zeitabhängigen) Winkel des Pendels und des Fahrzeugs gleich groß sein. Das ist der Fall, wenn beide Winkelgeschwindigkeitsänderungen identisch sind. In

{\frac {\mathrm {d} \omega _{\text{P}}}{\mathrm {d} t}}={\frac {R_{\text{E}}}{a}}{\frac {\mathrm {d} \omega _{\text{F}}}{\mathrm {d} t}}

muss somit

{\frac {R_{\text{E}}}{a}}=1

gelten. Das bedeutet, dass die Pendellänge gleich dem Erdradius sein muss:

R_{\text{E}}=a

Die Schwingungsdauer eines Pendels mit der Länge L ist gegeben durch (g=Erdbeschleunigung von 9,81 m/s²)

T=2\pi {\sqrt {\frac {L}{g}}}=2\pi {\sqrt {\frac {R_{\text{E}}}{g}}}=84,4

min

Das ist die Schuler-Periode.

Anwendungen

Lotpendel

Eine hypothetische Kanonenkugel, die die Erde im kleinstmöglichen Orbit umkreist (D), hätte die Umlaufdauer der Schuler-Periode und die erste kosmische Geschwindigkeit.

Schuler war mit der Optimierung von der Navigation dienenden Kreiselgeräten befasst. Er ging davon aus, dass die Abstimmung solcher Geräte mit der Zeitdauer von 84 Minuten zu einer Minimierung von Beschleunigungsfehlern führen würde. Ein allgemeiner Beweis gelang ihm nicht (und ist auch nicht möglich), jedoch konnte er die Gültigkeit für den Lotkreisel (Kreiselpendel) und den Kreiselkompass (nordsuchender Kompass) in seiner o. g. Schrift (z. T. nochmals) nachweisen. Die Untersuchung zum Lotkreisel hatte die Firma Anschütz, bei der Schuler tätig war, schon Jahre zuvor als Patentschrift eingereicht.[5] Die Veröffentlichung von 1923 war also insbesondere für die weitere Entwicklung des Kreiselkompasses bedeutsam.

Die praktische Umsetzung der Schuler-Abstimmung ist mit technischen Problemen verknüpft (extrem hohe Drehzahl erforderlich). Schuler hatte zum Zeitpunkt seiner Veröffentlichung eine Umlaufzeit von T = 30 Minuten erreicht.

Das Schuler-Kriterium bildet die Basis für die Optimierung (Abstimmung) der vielfältigen Geräte der Kreiselnavigation (z. B. Trägheitsplattform, Künstlicher Horizont usw.).

Lotkreisel

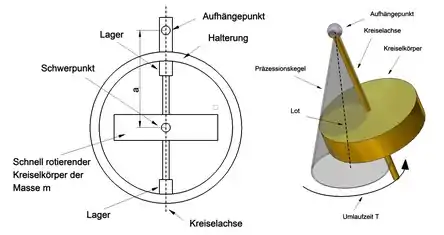
Ein Lotkreisel besteht aus einer sich mit hoher Drehzahl drehenden rotationssymmetrischen Schwungmasse (elektromotorisch angetrieben) mit senkrechter Achse. Der Kreisel ist pendelartig an einem Aufhängepunkt befestigt. Die auf einen in nicht senkrechter Achsenlage befindlichen Kreisel wirkende Erdanziehung übt ein Drehmoment aus und sucht die Kreiselachse in die Vertikale zu ziehen. Der Kreisel reagiert darauf jedoch mit der sogenannten Präzession, d. h., er weicht seitlich aus und seine Achse bewegt sich mit konstanter Winkelgeschwindigkeit auf einer Kegelmantelfläche.

Die Dauer eines Umlaufs (Schwingungsdauer) ist gegeben durch (Kreiseltheorie):

T=2\pi {\frac {J}{mga}}

,

wobei J der Drehimpuls ist.

Schuler hat nachgewiesen, dass bei einer Umlaufdauer von 84 Minuten (Schuler-Abstimmung) das Lotpendel weitgehend unempfindlich gegenüber Beschleunigungseinflüssen ist und seine lotrechte Lage beibehält, sofern vor Eintritt der Beschleunigung sich die Achse in lotrechter Stellung befindet (keine Präzession vorhanden). Bevor ein Fahrzeug Fahrt aufnimmt, muss also die lotrechte Lage des Kreisels gewährleistet sein.

Kreiselkompass

Auch der Kreiselkompass (horizontale Kreiselachse) ist schwingfähig, jedoch im Gegensatz zum Pendel um eine senkrechte Achse, und kann mit der Schuler-Abstimmung (Schwingungsdauer 84 Minuten) optimiert werden. In der Praxis konstruiert man das System so, dass die Eigenschwingfrequenz mit der Schuler-Periode zusammenfällt [6].

Erläuterung [7]:

Der Kreiselkompass (Einkreiselkompass) ist nordsuchend. Die horizontale Kreiselachse stellt sich bei ruhendem Fahrzeug (Schiff) selbsttätig in Nord-Süd-Richtung ein (also in Meridianrichtung). Das dauert mehrere Stunden. Die Einstellung erfolgt dabei nicht durch einen gleichmäßigen Übergang, sondern ist durch einen abklingenden Schwingungsvorgang gekennzeichnet (mehrfaches Schwingen der Kreiselachse um die Nord-Süd-Richtung). Das Fahrzeug kann erst nach Abklingen der Schwingung seine Fahrt aufnehmen, wenn die Funktion des Kompasses gewährleistet werden soll.

Wenn sich das Fahrzeug mit einer bestimmten konstanten Geschwindigkeit in eine von der Ost-West-Richtung (oder umgekehrt) abweichende Richtung bewegt, weist der Kompass einen Fahrtfehler auf. Zu beachten ist, dass unter Geschwindigkeit die aus der vektoriellen Addition von Umfangsgeschwindigkeit der Erde (auf dem Breitengrad der Fahrzeugposition) und Geschwindigkeit des Fahrzeugs sich ergebende resultierende Geschwindigkeit zu verstehen ist. Die Kreiselachse zeigt nicht mehr exakt nach Norden, sondern stellt sich senkrecht zur resultierenden Geschwindigkeit ein. Bei einer Fahrt auf dem Breitengrad (also quer zur Meridianrichtung) tritt kein Fahrtfehler auf. Der geschwindigkeitsabhängige Fahrtfehler kann berechnet werden. Er ist in Tabellen festgehalten und kann somit vom Navigator korrigiert werden (heutzutage mit entsprechenden Computerprogrammen).

Wird das Fahrzeug mit einer Nord- bzw. Südkomponente beschleunigt, wirkt auf den Kreiselkompass (der pendelnd aufgehängt ist) ein Drehmoment, auf das der Kreisel mit einer entsprechenden Präzession reagiert (also einer Verdrehung um die senkrechte Achse). Wäre der Kreisel nicht nach Schuler abgestimmt, würde er sich nach Abschluss der Beschleunigung langsam (abklingend schwingend) auf den der geänderten Geschwindigkeit entsprechenden neuen Fahrtfehler einstellen. Der Navigator könnte also nicht sicher sein, wann der Ablesung wieder zu vertrauen ist. Dieser schwerwiegende Nachteil stellte vor der Veröffentlichung von Schuler die Verwendbarkeit von Kreiselkompassen generell in Frage. Ist das System jedoch nach Schuler abgestimmt, entspricht die durch die Präzession hervorgerufene Drehung der Kreiselachse um die Senkrechte genau dem Winkel der Fahrtfehleränderung. Es tritt keine Schwingung auf. Der neue Kurs (mit dem der veränderten Geschwindigkeit entsprechenden Fahrtfehler) kann unmittelbar nach dem Ende der Beschleunigungsphase abgelesen werden.

Da die Abstimmbedingung vom Breitengrad abhängt, muss der Kompass auf das jeweilige Operationsgebiet des Fahrzeugs abgestimmt werden. Der Kompass kann beispielsweise so konstruiert werden, dass das manuell durch Veränderung der (extrem kurzen) Pendellänge des pendelnd aufgehängten Kreisels geschehen und so die Schulerperiode eingestellt werden kann.

Die Abstimmbedingung lautet:

{\frac {J}{mga\cdot \omega _{E}\cdot \cos \phi }}={\frac {R_{E}}{g}}

{\phi }

Breitengrad, a zu variierende Pendellänge

Die Berechnungen zum Kreiselkompass sind ebenfalls in der bereits erwähnten Veröffentlichung von Schuler zu finden.

Nachfolgende Forschungen haben ergeben, dass das Schuler-Kriterium bei Kreiselgeräten nicht universell anwendbar ist. Insbesondere bei sich schnell ändernden Beschleunigungen (z. B. die Roll- und Gierbewegungen eines Schiffes, Schlingerfehler) sind davon abweichende Abstimmungen zweckmäßig (siehe dazu [8][9]) bzw. Zweikreiselkompasse[10] erforderlich. Auch kann nicht vernachlässigt werden, dass das Gravitationsfeld an der Erdoberfläche nicht, wie angenommen, homogen ist, sondern, wenn auch geringfügige, Abweichungen aufweist. Dies macht sich insbesondere bei der Satellitennavigation bemerkbar.

Sonstiges

Neben den Gegebenheiten bei Kreiselgeräten unterliegen auch andere Phänomene dem 84-Minuten-Kriterium. Z. B. beträgt die Umlaufdauer eines Satelliten auf der niedrigstmöglichen Bahn 84 Minuten. Weitere Beispiele siehe [11].

Einzelnachweise

Kurt Magnus: Kreisel: Theorie und Anwendungen. Springer Verlag.
Richard Grammel: Der Kreisel, Seine Theorie und seine Anwendungen: Zweiter Band. Springer Verlag, 1950.
Max Schuler: Pendel für Zeitmessungszwecke. (PDF) Abgerufen am 19. April 2019 (nach Aufruf "Volldokument laden" anklicken).
Maximilian Schuler: Die Störung von Pendel- und Kreiselapparaten durch die Beschleunigung des Fahrzeugs. (PDF) In: Physikalische Zeitschrift 24, Seite 344 (1923). Abgerufen am 22. September 2018 (englisch).
Kreiselhorizont. (PDF) Abgerufen am 14. März 2019 ("Volldokument laden" anklicken!).
Müller/Krauß: Handbuch für die Schiffsführung Teil B. Springer Verlag, Berlin 1983.
Terheyden, Zickwolff: Navigation Teil B. Springer-Verlag, Berlin Heidelberg.
Kurt Magnus: Die beschleunigungsunempfindliche Abstimmung von Navigationsgeräten. (PDF) Abgerufen am 4. Juli 2020.
Kurt Magnus: Die Beschleunigungsabhängigkeit der Vertikalenanzeige von Schwerependel und Lotkreisel. (PDF) In: Ingenieur-Archiv. 1966, abgerufen am 4. Juli 2020.
Mehrkreiselkompass. (PDF) Abgerufen am 13. März 2019 ("Volldokument laden" anklicken!).
Kurt Magnus: Kreisel als vielseitige Hilfsmittel in Luft- und Raumfahrt. (PDF) In: Zeitschrift für Flugwissenschaften und Weltraumforschung. Juli 1978, abgerufen am 4. Juli 2020.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Kurt Magnus: Kreisel: Theorie und Anwendungen. Springer Verlag.

[2] Richard Grammel: Der Kreisel, Seine Theorie und seine Anwendungen: Zweiter Band. Springer Verlag, 1950.

[3] Max Schuler: Pendel für Zeitmessungszwecke. (PDF) Abgerufen am 19. April 2019 (nach Aufruf "Volldokument laden" anklicken).

[4] Maximilian Schuler: Die Störung von Pendel- und Kreiselapparaten durch die Beschleunigung des Fahrzeugs. (PDF) In: Physikalische Zeitschrift 24, Seite 344 (1923). Abgerufen am 22. September 2018 (englisch).

[5] Kreiselhorizont. (PDF) Abgerufen am 14. März 2019 ("Volldokument laden" anklicken!).

[6] Müller/Krauß: Handbuch für die Schiffsführung Teil B. Springer Verlag, Berlin 1983.

[7] Terheyden, Zickwolff: Navigation Teil B. Springer-Verlag, Berlin Heidelberg.

[8] Kurt Magnus: Die beschleunigungsunempfindliche Abstimmung von Navigationsgeräten. (PDF) Abgerufen am 4. Juli 2020.

[9] Kurt Magnus: Die Beschleunigungsabhängigkeit der Vertikalenanzeige von Schwerependel und Lotkreisel. (PDF) In: Ingenieur-Archiv. 1966, abgerufen am 4. Juli 2020.

[10] Mehrkreiselkompass. (PDF) Abgerufen am 13. März 2019 ("Volldokument laden" anklicken!).

[11] Kurt Magnus: Kreisel als vielseitige Hilfsmittel in Luft- und Raumfahrt. (PDF) In: Zeitschrift für Flugwissenschaften und Weltraumforschung. Juli 1978, abgerufen am 4. Juli 2020.