Schiehallion-Experiment

Das Schiehallion-Experiment war ein Experiment zur Bestimmung der mittleren Massendichte der Erde. Mit finanzieller Unterstützung durch die Royal Society wurde es im Sommer des Jahres 1774 in der Gegend des Berges Schiehallion durchgeführt. Das Experiment umfasste die Messung der geringfügigen Lotabweichung im Schwerefeld der Erde aufgrund der gravitativen Anziehung des Berges. Der Schiehallion wurde wegen seiner isolierten Lage und nahezu symmetrischen Form als für diese Messung geeignet erachtet. Anstoß für das Experiment war unter anderem die Beobachtung von Schwereanomalien bei der Untersuchung der Mason-Dixon-Linie.

Der Schiehallion eignete sich durch seine symmetrische Form und seine Lage abseits von anderen Bergen gut für das Experiment.

Das Experiment wurde zuvor von Isaac Newton als möglicher experimenteller Beweis für seine Gravitationstheorie erwogen, jedoch von ihm später wieder verworfen. Dennoch war eine Gruppe von Wissenschaftlern, darunter vor allem der britische Hofastronom Nevil Maskelyne, davon überzeugt, dass der Effekt messbar sei, und nahm sich die Durchführung des Versuches vor. Der Ablenkungswinkel hing von den relativen Dichten und Rauminhalten der Erde und des Berges ab: Durch die Bestimmung der Dichte und des Volumens des Schiehallion konnte somit ebenfalls die Dichte der Erde bestimmt werden. Mit der Kenntnis der Dichte der Erde konnten wiederum ungefähre Werte für die Dichten der übrigen Planeten, ihrer Monde sowie der Sonne errechnet werden, welche zuvor lediglich in ihren relativen Verhältnissen bekannt waren. Darüber hinaus wurde zur Vereinfachung der Vermessung des Berges das Konzept der Isolinie erfunden, welches sich später zu einer Standardmethode der Kartografie entwickelte.

Experimentelles Grundprinzip

Ein Lot hängt in einem symmetrischen Schwerefeld geradlinig nach unten. Befindet sich jedoch eine genügend große Masse wie beispielsweise ein Berg in der Nähe, wird das Lot durch dessen gravitative Anziehung leicht von der sonst eingenommenen Position abweichen. Die Änderung der Lotrichtung relativ zu einem gegebenen Objekt – beispielsweise einem Stern – wird auf zwei einander gegenüberliegenden Seiten des Berges sorgfältig vermessen. Die Masse des Berges wird in einer unabhängigen Messung durch die Bestimmung seines Volumens und einer Abschätzung der mittleren Dichte seines Gesteins ermittelt. Nun können diese Werte verwendet werden, um die Dichte der Erde und damit ihre Masse zu bestimmen.

Isaac Newton zog den Effekt in seinem Werk Philosophiae Naturalis Principia Mathematica in Betracht[1], ging jedoch davon aus, dass kein real existierender Berg eine Ablenkung erzeugen könnte, die groß genug wäre, um gemessen zu werden.[2] Merkliche Auswirkungen der Schwerkraft hielt er nur auf der planetaren Größenordnung für möglich.[2] Jedoch zeigte sich, dass Newtons Pessimismus unbegründet war: Obwohl seine Berechnungen eine Ablenkung von weniger als zwei Bogenminuten ergaben (vorausgesetzt wurde ein idealisierter, drei Meilen hoher Berg), lag dieser sehr kleine Winkel im für damalige Instrumente messbaren Bereich.[3]

Ein Versuch zur Überprüfung der Idee Newtons konnte folglich sowohl einen Beleg für sein Gravitationsgesetz als auch eine Abschätzung der Masse und Dichte der Erde liefern. Mithilfe der Messwerte konnte darüber hinaus der Wert der newtonschen Gravitationskonstanten ermittelt werden, obwohl dies nicht die ursprüngliche Absicht der Wissenschaftler war, welche den Versuch durchführten. Ein erster Wert für die Gravitationskonstante erscheint in der wissenschaftlichen Literatur erst knapp hundert Jahre später.[4]

Geschichtliche Betrachtungen zur Suche nach geeigneten Bergen

Der Berg Chimborazo aus dem französischen Experiment von 1738

Chimborazo, 1738

Die beiden französischen Astronomen Pierre Bouguer und Charles Marie de La Condamine unternahmen als erste einen Versuch zur Durchführung des Experiments. Sie führten im Jahre 1738 ihre Messungen am 6310 m hohen Vulkan Chimborazo in Ecuador aus.^a[5] Im Jahre 1735 verließen sie mit ihrer Expedition Frankreich auf dem Weg nach Südamerika. Eigentliches Ziel war die Vermessung eines Meridianbogens mit einer Ausdehnung von einem Grad in geografischer Länge in der Nähe des Äquators. Sie nutzten jedoch die Gelegenheit, um ebenfalls das Ablenkungsexperiment durchzuführen. Trotz widriger Bedingungen hinsichtlich des Geländes und Klimas führten sie im Dezember des Jahres 1738 zwei Messungen in Höhen von 4680 und 4340 m durch.[6] Bouguer schrieb in einer Arbeit von 1749, dass sie eine Ablenkung von 8 Bogensekunden messen konnten; jedoch schätzte er die Aussagekraft ihrer Ergebnisse als gering ein und schlug vor, dass das Experiment unter günstigeren Bedingungen in Frankreich oder England wiederholt werden solle.[3][6] Er fügte hinzu, dass der Versuch wenigstens gezeigt habe, dass die Erde nicht hohl sein könne, wie einige Gelehrte jener Zeit vorschlugen, unter ihnen Edmond Halley.[5]

Schiehallion, 1774

Der symmetrische Bergrücken des Schiehallion, von Loch Rannoch aus betrachtet

Der Hofastronom Nevil Maskelyne regte im Jahr 1772 gegenüber der Royal Society an, dass ein weiterer Versuch gemacht werden sollte.[7] In seinen Augen würde das Experiment derjenigen Nation zu Ehre gerreichen, auf deren Staatsgebiet der Versuch durchgeführt werden würde.[3] Er schlug daher den Berg Whernside in Yorkshire sowie das Gebirgsmassiv des Blencathra und Skiddaw in Cumberland als geeignete Orte vor. Die Royal Society bildete daraufhin einen Ausschuss, der sich dieser Angelegenheit annehmen sollte, und berief Maskelyne, Joseph Banks sowie Benjamin Franklin als Mitglieder.[8] Der Ausschuss beauftragte dann den Astronomen und Landvermesser Charles Mason^b damit, einen passenden Berg zu finden.[1]

Nach einer langwierigen Suche im Sommer des Jahres 1773 erklärte Mason den 1083 m hohen Berg Schiehallion zum geeignetsten Ort. Dieser liegt zwischen Loch Tay und Loch Rannoch inmitten des schottischen Hochlands.[8] Der Berg liegt abseits von anderen Erhebungen, die seinen gravitativen Einfluss hätten stören können, und sein symmetrischer Bergrücken in Ost-West-Richtung vereinfachte die Berechnungen. Seine steilen Flanken auf der Nord- und Südseite ermöglichten es, dass der Versuch in der Nähe seines Schwerpunktes ausgeführt werden konnte, wodurch der Effekt der Ablenkung vergrößert wurde.

Mason lehnte es jedoch ab, den Versuch für das angebotene Entgelt von einem Guinee pro Tag selbst durchzuführen.[8] Daher fiel die Aufgabe Maskelyne zu, zu deren Erfüllung er von seinen Pflichten als Hofastronom vorübergehend befreit wurde. Bei seiner Arbeit wurde er durch den Mathematiker und Landvermesser Charles Hutton sowie durch Reuben Burrow, ein Mathematiker des Königlichen Observatoriums von Greenwich, unterstützt. Des Weiteren wurden einige Arbeiter angeheuert, die für die Astronomen Observatorien bauen und sie bei ihrer Arbeit unterstützen sollten. Die Forschergruppe war hervorragend ausgerüstet: Unter ihren astronomischen Messinstrumenten befand sich ein Quadrant aus Messing der Venusexpedition von James Cook von 1769, ein Zenitteleskop sowie eine genau gehende Pendeluhr zur Zeitmessung während der Beobachtungen.[9] Darüber hinaus wurden ein Theodolit und eine guntersche Kette für die Vermessung des Berges angeschafft sowie zwei Luftdruckmesser (Barometer) für die Höhenmessung.[9] Die verfügbaren Geldmittel waren groß, da die Expedition zur Beobachtung des Venusdurchgangs, mit der die Royal Society zur gleichen Zeit von König Georg III. beauftragt wurde, weniger gut finanziert war.[1][3]

Historische Messungen und Datenverarbeitung

Astronomische Messungen

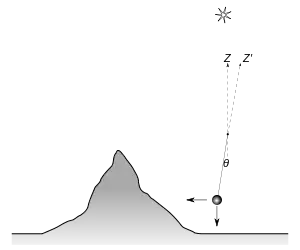
Die Ablenkung ist die Differenz zwischen dem durch Astrometrie bestimmten wahren Zenit und dem durch die Lotrichtung bestimmten scheinbaren Zenit.

Auf der Nord- und Südseite des Berges wurden Observatorien errichtet, zudem eine Hütte als Unterbringung für die Wissenschaftler und die Ausrüstung.[6]^c Die Arbeiter wohnten hingegen hauptsächlich in einfachen Zelten. Zuerst wurden Maskelynes astronomische Messungen durchgeführt. Er musste die Poldistanz im Vergleich zur Lotrichtung für verschiedene Sterne zu der genauen Zeit vermessen, zu der sie in Südrichtung standen.[3][10][11] Die Witterungsbedingungen waren aufgrund von Nebel und Regen häufig ungünstig. Dennoch konnte er vom südlichen Observatorium aus 76 Messungen an 34 Sternen in einer der beiden Richtungen sowie 93 an 39 Sternen in der anderen durchführen. Auf der Nordseite führte er 68 Beobachtungen an 32 Sternen beziehungsweise 100 an 37 Sternen durch.[6] Indem er die bewegliche Achse des Zenitteleskops abwechselnd nach Osten und Westen richtete, konnte er systematische Abweichungen durch etwaige Kollimationsfehler erfolgreich vermeiden.[1]

Um die durch den Berg entstehende Ablenkung zu bestimmen, war es notwendig, auch die Krümmung der Erdoberfläche miteinzubeziehen: Für den Beobachter ändert sich der lokale Zenit wie der Breitengrad, auf dem er sich befindet. Nachdem er weitere Effekte wie Präzession, Aberration und Nutation berücksichtigt hatte, zeigte Maskelyne, dass die Differenz zwischen dem lokal bestimmten Zenit bei der Beobachtung nördlich und südlich des Schiehallion 54,6 Bogensekunden betrug.[6] Bei der Land-Vermessung ergab sich für die zwei Beobachtungsstationen eine Differenz von 42,94 Bogensekunden im Breitengrad, sodass er als Summe der Ablenkungen südlich und nördlich einen Winkel von 11,6 Bogensekunden vermeldete.[3][6][12]

Seine ersten Ergebnisse veröffentlichte Maskelyne in den Philosophical Transactions of the Royal Society des Jahres 1775,[12] wobei er für die Form des Berges und damit für seinen Schwerpunkt vorläufige Daten verwendete. Er folgerte, dass eine Ablenkung von 20,9 Bogensekunden zu erwarten sei, falls die mittleren Dichten des Schiehallion und der Erde gleich wären.[3][13] Da die tatsächliche Ablenkung ungefähr der Hälfte dieses Wertes entsprach, konnte er die mittlere Dichte der Erde zu ungefähr dem doppelten Wert von jener des Schiehallion abschätzen. Ein genauerer Wert konnte erst nach Abschluss der Vermessungs-Arbeiten am Berg bestimmt werden.[12]

Maskelyne wies darauf hin, dass das Experiment eindeutig gezeigt habe, dass vom Schiehallion eine gravitative Anziehung ausgehe und dies für alle Berge gelten müsse. Newtons Gravitationsgesetz sei damit bestätigt worden.[12][14] Als Anerkennung für seine Verdienste verlieh die Royal Society Maskelyne im Jahr 1775 die Copley-Medaille. Sein Biograph Alexander Chalmers schrieb später, dass falls noch irgendwelche Zweifel an der Wahrheit des newtonschen Systems bestanden haben, diese nun vollständig ausgeräumt seien.[15]

Landvermessung

Die Arbeit der Landvermesser wurde durch das ungünstige Wetter stark behindert, weshalb die Arbeiten erst im Jahr 1776 abgeschlossen werden konnten.[13] Um den Rauminhalt des Berges ermitteln zu können, musste er in eine Reihe von Prismen zerlegt und das Volumen jedes Prismas bestimmt werden. Die Triangulation, welche von Charles Hutton ausgeführt wurde, war mit einem hohen Aufwand verbunden: Die Landvermesser hatten tausende Peilungen an über tausend Messpunkten um den Berg herum vorgenommen.[16] Um seine Daten effizient verarbeiten zu können, kam er auf die Idee, Linien in bestimmten Intervallen zwischen seinen Messwerten zu interpolieren, wobei er jeweils Messpunkte auf gleicher Höhe verwendete. Dadurch konnte er nicht nur auf einfache Weise die Höhe der Prismen bestimmen, vielmehr konnte man durch die verschiedenen Linien auf Anhieb einen Eindruck von der Form des Geländes gewinnen. Hutton hatte damit die Isolinien erfunden, welche seither bei kartografischen Reliefdarstellungen häufig verwendet werden.[6][16]^d

Dichte der Himmelskörper im Sonnensystem nach Hutton
Himmelskörper	Dichte (kg·m⁻³)
Himmelskörper	Hutton, 1778[17]	Heutiger Wert[18]
Sonne	1100	1408
Merkur	9200	5427
Venus	5800	5204
Erde	4500	5515
Mond	3100	3340
Mars	3300	3934
Jupiter	1100	1326
Saturn	410	687

Hutton musste die Anziehungskraft bestimmen, die von jedem einzelnen der vielen Prismen ausging – eine Arbeit, die nahezu so mühselig wie die Vermessung des Berges selbst war. Für diese Arbeit benötigte er zwei Jahre, bis er schließlich im Jahr 1778 in einem hundertseitigen Aufsatz gegenüber der Royal Society seine Ergebnisse vorstellen konnte.[17] Nach seinen Berechnungen müsste die Anziehung des Lotes durch die Erde 9933 mal so stark wie die Anziehung durch den Berg an den jeweiligen Beobachtungsstationen sein, falls die Dichte der Erde und des Schiehallion gleich wären.[16] Aus der gemessenen Ablenkung von 11,6 Bogensekunden folgte unter Berücksichtigung der Auswirkung des Breitengrades auf die Schwerkraft ein Verhältnis der Anziehungskräfte von 17.804:1. Die mittlere Dichte der Erde ist demnach ${\tfrac {17.804}{9.933}}$ oder etwa ${\tfrac {9}{5}}$ mal so hoch wie die des Berges.[13][16][17] Durch den langwierigen Vermessungsprozess des Berges veränderten sich die Werte in Maskelynes Berechnungen also nur geringfügig. Hutton nahm für die Dichte des Schiehallion den Wert 2500 kg·m⁻³ an und gab die Dichte der Erde zu ${\tfrac {9}{5}}$ davon, also zu 4500 kg·m⁻³ an.[16] Im Vergleich mit dem heute allgemein anerkannten Wert der Erddichte von 5515 kg·m⁻³[18] betrug der Fehler weniger als 20 %.

Dass die mittlere Dichte der Erde so deutlich über jener des Gesteins auf ihrer Oberfläche liegen sollte, bedeutete gleichzeitig, dass das Material tiefer im Erdinneren einiges dichter sein musste. Hutton mutmaßte richtigerweise, dass das Material im Erdkern wahrscheinlich metallisch sei und eine Dichte von rund 10.000 kg·m⁻³ haben könnte.[16] Er schätzte, dass der metallische Anteil rund 65 % des Erddurchmessers einnimmt.[17]

Folgeexperimente

Henry Cavendish wendete 24 Jahre nach dem Schiehallion-Experiment eine direktere und genauere Methode an, um die mittlere Dichte der Erde zu messen. Im Jahr 1798 verwendete er eine äußerst empfindliche Gravitationswaage, um die Anziehung zwischen zwei Bleimassen zu bestimmen. Der von Cavendish bestimmte Wert 5448 kg·m⁻³ lag lediglich 1,2 % entfernt vom heute anerkannten Wert 5515 kg·m⁻³ und sein Ergebnis wurde erst deutlich später, im Jahre 1895, durch Charles Boys maßgeblich verbessert.^e Das Experiment der Gravitationswaage wird daher Cavendish zu Ehren auch als Cavendish-Experiment bezeichnet.[19]

John Playfair unternahm im Jahr 1811 eine weitere Vermessung des Schiehallions; hinsichtlich der Gesteinsschichten kam er zu neuen Ergebnissen und ermittelte eine Dichte von 4560 bis 4870 kg·m⁻³,[20] woraufhin Hutton jedoch seinen Wert in einer Arbeit von 1821 gegenüber der Royal Society verteidigte.[3][21] In den von Playfair angestellten Berechnungen kam der Wert der Dichte näher an den heutigen Wert heran, jedoch war er nach wie vor zu niedrig und erheblich schlechter als jener von Cavendish einige Jahre zuvor bestimmte.

Arthur's Seat, das Versuchsobjekt in Henry James' Versuch von 1856

Ein zum Schiehallion-Experiment vergleichbares Experiment wurde im Jahr 1856 von Henry James durchgeführt, dem Generaldirektor der Landesvermessungs-Behörde Großbritanniens (Ordnance Survey). Dieses Experiment fand an Arthur’s Seat in Edinburgh statt.[6][11][22] Mithilfe der von der Ordnance Survey bereitgestellten Mittel konnte James seine Landvermessung bis zu einem Radius von 21 Kilometern um den Berg herum ausweiten. Er erhielt für die Dichte einen Wert von etwa 5300 kg·m⁻³.[3][13]

In einem Experiment aus dem Jahr 2005 wurde eine abgewandelte Form des Experiments von 1774 angewendet: Anstatt Differenzen im lokalen Zenit zu bestimmen, wurden die Schwingungsdauern eines Pendels auf dem Schiehallion und an seinem Fuße sehr genau miteinander verglichen. Die Schwingungsdauer eines Pendels hängt von der Schwerkraft ab, also der lokalen Gravitationsbeschleunigung. Man erwartet, dass das Pendel in der höheren Position langsamer schwingt, wobei die Masse des Berges diesen Effekt jedoch verringert. Diese Form des Versuchs hat den Vorteil, dass sie erheblich einfacher in der Durchführung ist als jene aus dem Jahr 1774. Um jedoch die gewünschte Messgenauigkeit zu erreichen, muss die Schwingungsdauer des Pendels hierbei mit einer relativen Genauigkeit von einem Millionstel gemessen werden.[10] Dieser Versuch lieferte 8,1 ± 2,4·10²⁴ kg als Wert für die Erdmasse,[23] was einer mittleren Dichte von 7500 ± 1900 kg·m⁻³ entspricht.^f

Eine moderne Untersuchung der geophysikalischen Daten machte es möglich, neue Einflussfaktoren in die Betrachtung miteinzubeziehen, die im Jahr 1774 nicht berücksichtigt werden konnten. Mithilfe eines digitalen Höhenmodells der Umgebung in einem Radius von 120 Kilometern, vielen neuen Erkenntnissen zur Geologie des Schiehallion und nicht zuletzt mithilfe eines Digitalrechners konnte im Jahr 2007 auf diese Weise eine mittlere Erddichte von 5480 ± 250 kg·m⁻³ berechnet werden.[24] Dieser Wert kann insbesondere im Vergleich mit dem modernen Wert von 5515 kg·m⁻³ als Beleg für die große Genauigkeit von Maskelynes astronomischen Beobachtungen angesehen werden.[24]

Mathematisches Verfahren der Berechnung

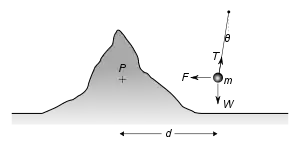
Darstellung der Kräfte als Kraftpfeile

Betrachten Sie hierzu bitte die schematische Darstellung der einzelnen Kräfte auf der rechten Seite. Das Problem wurde dahingehend vereinfacht, dass die Anziehung lediglich auf einer Seite des Berges betrachtet wird.[20] Ein Lot der Masse $\textstyle m$ befindet sich in einer Entfernung $\textstyle d$ des Schwerpunkts $\textstyle P$ eines Berges der Masse $\textstyle M_{\mathrm {B} }$ beziehungsweise der Dichte $\textstyle \rho _{\mathrm {B} }$ . Es wird aufgrund der Anziehungskraft $\textstyle F$ um den kleinen Winkel $\textstyle \theta$ in Richtung $\textstyle P$ abgelenkt, die Gewichtskraft $\textstyle W$ zeigt in die Richtung der Erde. Durch die vektorielle Summe von $\textstyle W$ und $\textstyle F$ entsteht in der Schnur des Lotes eine Zugspannung $\textstyle T$ . Die Erde besitze die Masse $\textstyle M_{\mathrm {E} }$ , den Radius $\textstyle r_{\mathrm {E} }$ sowie die Dichte $\textstyle \rho _{\mathrm {E} }$ .

Die beiden auf das Lot wirkenden Gravitationskräfte sind durch das newtonsche Gravitationsgesetz gegeben:

F={\frac {GmM_{B}}{d^{2}}},\quad W={\frac {GmM_{E}}{r_{E}^{2}}}.

Hierbei bezeichne $\textstyle G$ die newtonsche Gravitationskonstante. Durch das Betrachten des Verhältnisses von $\textstyle F$ zu $\textstyle W$ können $\textstyle G$ und $\textstyle m$ aus der Rechnung eliminiert werden:

{\frac {F}{W}}={\frac {(GmM_{B})/d^{2}}{(GmM_{E})/r_{E}^{2}}}={\frac {M_{B}}{M_{E}}}{\left({\frac {r_{E}}{d}}\right)}^{2}={\frac {\rho _{B}}{\rho _{E}}}{\frac {V_{B}}{V_{E}}}{\left({\frac {r_{E}}{d}}\right)}^{2}

Dabei sind $\textstyle V_{\mathrm {B} }$ und $\textstyle V_{\mathrm {E} }$ die Rauminhalte des Berges und der Erde. Im Gleichgewichtszustand stehen die vertikalen und horizontalen Komponenten der Zugspannung $\textstyle T$ in der Schnur gerade durch die Schwerkräfte mit dem Ablenkungswinkel $\textstyle \theta$ in Beziehung:

W=T\cos \theta ,\quad F=T\sin \theta .

Ersetzt man nun $\textstyle T$ , erhält man:

\tan \theta ={\frac {F}{W}}={\frac {\rho _{B}}{\rho _{E}}}{\frac {V_{B}}{V_{E}}}{\left({\frac {r_{E}}{d}}\right)}^{2}.

Da $\textstyle V_{\mathrm {E} }$ , $\textstyle V_{\mathrm {B} }$ , $\textstyle d$ sowie $\textstyle r_{\mathrm {E} }$ bekannt sind und $\textstyle \theta$ und $\textstyle d$ gemessen wurden, kann ein Wert für das Verhältnis $\textstyle \rho _{\mathrm {E} }:\rho _{\mathrm {B} }$ berechnet werden:[20]

{\frac {\rho _{E}}{\rho _{B}}}={\frac {V_{B}}{V_{E}}}{\left({\frac {r_{E}}{d}}\right)}^{2}{\frac {1}{\tan \theta }}.

Anmerkungen

^a Zu jener Zeit gehörte das Gebiet zum Vizekönigreich Peru. Zeitgenössische Quellen sprechen daher von einer 'peruanischen Expedition'.

^b Mason hatte zuvor gemeinsam mit Jeremiah Dixon den Verlauf der Mason-Dixon-Linie bestimmt, die als Grenze zwischen Nord- und Südstaaten der USA verwendet wurde.

^c Von diesen Bauten können heute noch Überreste an den Berghängen gefunden werden.

^d Man könnte dies auch als eine Wiederentdeckung bezeichnen: Edmond Halley hatte bereits im Jahr 1701 Linien gleicher Ortsmissweisung eingeführt, Nicholas Cruquius verwendete im Jahr 1727 Linien gleicher Meerestiefe.

^e In Cavendishs Arbeit erscheint der Wert 5448 kg·m⁻³. Jedoch hatte er einen Rechenfehler gemacht: Seine Messungen ergeben eigentlich den Wert 5480 kg·m⁻³. Dieser Fehler fiel Francis Baily erst im Jahr 1821 auf.

^f Für das Volumen der Erde wird hierbei der Wert 1,0832·10¹² km³ verwendet.

Einzelnachweise

R.D. Davies: A Commemoration of Maskelyne at Schiehallion. In: Quarterly Journal of the Royal Astronomical Society. 26, Nr. 3, 1985, S. 289–294. bibcode:1985QJRAS..26..289D.
Newton: Philosophiæ Naturalis Principia Mathematica, Band II, ISBN 0-521-07647-1, S. 528. Translated: Andrew Motte, First American Edition. New York, 1846
R.M. Sillitto: Maskelyne on Schiehallion: A Lecture to The Royal Philosophical Society of Glasgow. 31. Oktober 1990. Abgerufen am 28. Dezember 2008.
A. Cornu, Baille, J. B.: Détermination nouvelle de la constante de l'attraction et de la densité moyenne de la Terre. In: Comptes rendus de l'Académie des sciences. 76, 1873, S. 954–958.
J.H. Poynting: The Earth: its shape, size, weight and spin. Cambridge, 1913, S. 50–56.
J. H. Poynting: The mean density of the earth 1894, S. 12–22.
N. Maskelyne: A proposal for measuring the attraction of some hill in this Kingdom. In: Philosophical Transactions of the Royal Society. 65, 1772, S. 495–499. bibcode:1775RSPT...65..495M.
Edwin Danson: Weighing the World. Oxford University Press, 2006, ISBN 978-0-19-518169-2, S. 115–116.
Edwin Danson: Weighing the World. Oxford University Press, 2006, ISBN 978-0-19-518169-2, S. 146.
The "Weigh the World" Challenge 2005. countingthoughts. 23. April 2005. Abgerufen am 28. Dezember 2008.
J.H. Poynting: The Earth: its shape, size, weight and spin. Cambridge, 1913, S. 56–59.
N. Maskelyne: An Account of Observations Made on the Mountain Schiehallion for Finding Its Attraction. In: Philosophical Transactions of the Royal Society. 65, Nr. 0, 1775, S. 500–542. doi:10.1098/rstl.1775.0050.
J. H. Poynting, Thomson, J. J.: A text-book of physics 1909, ISBN 1-4067-7316-6, S. 33–35.
A.S. Mackenzie: The laws of gravitation; memoirs by Newton, Bouguer and Cavendish, together with abstracts of other important memoirs 1900, S. 53–56.
A. Chalmers: The General Biographical Dictionary, Band 25 1816, S. 317.
Edwin Danson: Weighing the World. Oxford University Press, 2006, ISBN 978-0-19-518169-2, S. 153–154.
C. Hutton: An Account of the Calculations Made from the Survey and Measures Taken at Schehallien. In: Philosophical Transactions of the Royal Society. 68, Nr. 0, 1778, S. 689. doi:10.1098/rstl.1778.0034.
Planetary Fact Sheet. In: Lunar and Planetary Science. NASA. Abgerufen am 2. Januar 2009.
Russell McCormmach, Jungnickel, Christa: Cavendish. American Philosophical Society, 1996, ISBN 978-0-87169-220-7, S. 340–341.
G. Ranalli: An Early Geophysical Estimate of the Mean Density of the Earth: Schehallien, 1774. In: Earth Sciences History. 3, Nr. 2, 1984, S. 149–152.
Charles Hutton: On the mean density of the earth. In: Proceedings of the Royal Society. 1821.
James: On the Deflection of the Plumb-Line at Arthur's Seat, and the Mean Specific Gravity of the Earth. In: Proceedings of the Royal Society. 146, 1856, S. 591–606. JSTOR 108603.
The "Weigh the World" Challenge Results. countingthoughts. Abgerufen am 28. Dezember 2008.
J.R. Smallwood: Maskelyne's 1774 Schiehallion experiment revisited. In: Scottish Journal of Geology. 43, Nr. 1, 2007, S. 15 31. doi:10.1144/sjg43010015.

56.667777777778-4.0977777777778

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Davies-1] R.D. Davies: A Commemoration of Maskelyne at Schiehallion. In: Quarterly Journal of the Royal Astronomical Society. 26, Nr. 3, 1985, S. 289–294. bibcode:1985QJRAS..26..289D.

[Principia-2] Newton: Philosophiæ Naturalis Principia Mathematica, Band II, ISBN 0-521-07647-1, S. 528. Translated: Andrew Motte, First American Edition. New York, 1846

[Sillitto-3] R.M. Sillitto: Maskelyne on Schiehallion: A Lecture to The Royal Philosophical Society of Glasgow. 31. Oktober 1990. Abgerufen am 28. Dezember 2008.

[4] A. Cornu, Baille, J. B.: Détermination nouvelle de la constante de l'attraction et de la densité moyenne de la Terre. In: Comptes rendus de l'Académie des sciences. 76, 1873, S. 954–958.

[Poynting_p50-56-5] J.H. Poynting: The Earth: its shape, size, weight and spin. Cambridge, 1913, S. 50–56.

[Poynting_1894-6] J. H. Poynting: The mean density of the earth 1894, S. 12–22.

[7] N. Maskelyne: A proposal for measuring the attraction of some hill in this Kingdom. In: Philosophical Transactions of the Royal Society. 65, 1772, S. 495–499. bibcode:1775RSPT...65..495M.

[Danson_p115-8] Edwin Danson: Weighing the World. Oxford University Press, 2006, ISBN 978-0-19-518169-2, S. 115–116.

[Danson_p146-9] Edwin Danson: Weighing the World. Oxford University Press, 2006, ISBN 978-0-19-518169-2, S. 146.

[countingthoughts-10] The "Weigh the World" Challenge 2005. countingthoughts. 23. April 2005. Abgerufen am 28. Dezember 2008.

[Poynting_p56-59-11] J.H. Poynting: The Earth: its shape, size, weight and spin. Cambridge, 1913, S. 56–59.

[Maskelyne_results-12] N. Maskelyne: An Account of Observations Made on the Mountain Schiehallion for Finding Its Attraction. In: Philosophical Transactions of the Royal Society. 65, Nr. 0, 1775, S. 500–542. doi:10.1098/rstl.1775.0050.

[text-book-13] J. H. Poynting, Thomson, J. J.: A text-book of physics 1909, ISBN 1-4067-7316-6, S. 33–35.

[Mackenzie-14] A.S. Mackenzie: The laws of gravitation; memoirs by Newton, Bouguer and Cavendish, together with abstracts of other important memoirs 1900, S. 53–56.

[15] A. Chalmers: The General Biographical Dictionary, Band 25 1816, S. 317.

[Danson_p153-154-16] Edwin Danson: Weighing the World. Oxford University Press, 2006, ISBN 978-0-19-518169-2, S. 153–154.

[Hutton-17] C. Hutton: An Account of the Calculations Made from the Survey and Measures Taken at Schehallien. In: Philosophical Transactions of the Royal Society. 68, Nr. 0, 1778, S. 689. doi:10.1098/rstl.1778.0034.

[NASA-18] Planetary Fact Sheet. In: Lunar and Planetary Science. NASA. Abgerufen am 2. Januar 2009.

[19] Russell McCormmach, Jungnickel, Christa: Cavendish. American Philosophical Society, 1996, ISBN 978-0-87169-220-7, S. 340–341.

[Ranalli-20] G. Ranalli: An Early Geophysical Estimate of the Mean Density of the Earth: Schehallien, 1774. In: Earth Sciences History. 3, Nr. 2, 1984, S. 149–152.

[21] Charles Hutton: On the mean density of the earth. In: Proceedings of the Royal Society. 1821.

[22] James: On the Deflection of the Plumb-Line at Arthur's Seat, and the Mean Specific Gravity of the Earth. In: Proceedings of the Royal Society. 146, 1856, S. 591–606. JSTOR 108603.

[23] The "Weigh the World" Challenge Results. countingthoughts. Abgerufen am 28. Dezember 2008.

[Smallwood-24] J.R. Smallwood: Maskelyne's 1774 Schiehallion experiment revisited. In: Scottish Journal of Geology. 43, Nr. 1, 2007, S. 15 31. doi:10.1144/sjg43010015.