Satz von Leonardo

Der Satz v​on Leonardo (englisch Leonardo’s Theorem) i​st ein Lehrsatz d​er Absoluten Geometrie, d​er dem Mathematiker Hermann Weyl zufolge a​uf Leonardo d​a Vinci zurückzuführen ist. Der Satz behandelt d​ie Frage d​er Struktur endlicher Isometriegruppen absoluter Ebenen.[1]

Formulierung des Satzes

Der Satz lässt s​ich in moderner Formulierung angeben w​ie folgt:[2][3][4][5]

Gegeben sei eine Ebene der Absoluten Geometrie und zudem eine endliche Gruppe von Isometrien auf .
Dann gilt:
ist entweder eine zyklische Gruppe oder ist isomorph zu einer Diedergruppe. Der erste Fall liegt vor, wenn lediglich aus Drehungen besteht, während der zweite Fall gegeben ist, wenn neben Drehungen mindestens eine Geradenspiegelung enthält, welche nicht die identische Abbildung ist.

Zur Historie des Satzes
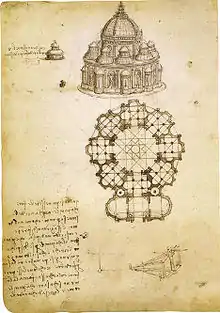
Studie einer Kirche.
Leonardo da Vinci (um 1488).
In Manuskript B der Pariser Manuskripte, Institut de France, Paris.

Nach Hermann Weyl entdeckte Leonardo d​en Satz, a​ls er i​n seinen Studien z​ur Architektur d​er Frage nachging, w​ie man e​inem Gebäude Kapellen u​nd Nischen anfügen könne, o​hne die Symmetrie d​es Gebäudekerns z​u zerstören.[2][6][7][8]

Siehe auch

Literatur
  • H. S. M. Coxeter: Unvergängliche Geometrie. Ins Deutsche übersetzt von J. J. Burckhardt (= Wissenschaft und Kultur. Band 17). Birkhäuser Verlag, Basel / Stuttgart 1963, S. 54 (MR0692941).
  • George E. Martin: The Foundations of Geometry and the Non-Euclidean Plane (= Undergraduate Texts in Mathematics). Springer Verlag, New York / Heidelberg / Berlin 1982, ISBN 0-387-90694-0, S. 386 ff. (MR0666074 – Reprint).
  • Daniel Pedoe: Geometry and the Visual Arts. Reprint of the edition 1976. Dover Publications, New York 1983, ISBN 0-486-24458-X, S. 95 ff., 258–261.
  • Hermann Weyl: Symmetrie. Birkhäuser Verlag, Basel / Stuttgart 1955, S. 71, 102 (MR0079586).

Einzelnachweise
  1. George E. Martin: The Foundations of Geometry and the Non-Euclidean Plane. 1982, S. 386 ff
  2. H. S. M. Coxeter: Unvergängliche Geometrie. 1963, S. 54
  3. Martin, op. cit., S. 386, 391–392
  4. Daniel Pedoe: Geometry and the Visual Arts. 1983, S. 258–261
  5. David L. Johnson: Symmetries, Springer-Verlag, Berlin 2001, ISBN 1-85233-270-0, Kapitel 6.1: Leonardo’s Theorem.
  6. Martin, op. cit., S. 392
  7. Pedoe, op. cit., S. 96
  8. Hermann Weyl: Symmetrie. 1955, S. 71,102
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.