Rotationszahl

Die Rotationszahl i​st eine Invariante v​on Selbstabbildungen d​es Kreises, d​ie erstmals v​on Henri Poincaré 1885 i​n seinen Arbeiten z​ur Himmelsmechanik untersucht wurde. Homöomorphismen v​on Kreisen kommen d​ort als Poincaré-Abbildungen (return maps) 2-dimensionaler Flüsse v​or und d​ie Rotationszahl d​er Poincaré-Abbildung liefert Informationen über d​as Langzeitverhalten d​es 2-dimensionalen Flusses.

Überlagerung des Kreises ${\displaystyle X=S^{1}=\mathbb {R} /\mathbb {Z} }$ durch die Zahlengerade ${\displaystyle Y=\mathbb {R} }$. Jede stetige Abbildung ${\displaystyle f\colon S^{1}\to S^{1}}$ kann zu einer stetigen Abbildung ${\displaystyle F\colon \mathbb {R} \to \mathbb {R} }$ mit ${\displaystyle F(x+m)=F(x)+m}$ für alle ${\displaystyle m\in \mathbb {Z} }$ hochgehoben werden.

Definition

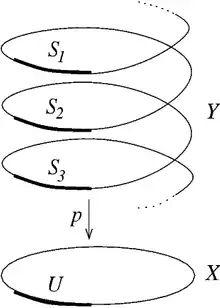
Es sei ${\displaystyle f\colon S^{1}\to S^{1}}$ ein orientierungserhaltender Homöomorphismus des Kreises ${\displaystyle S^{1}=\mathbb {R} /\mathbb {Z} }$ (vgl. Kreisgruppe). Dann gibt es eine Hochhebung von ${\displaystyle f}$ zu einem Homöomorphismus ${\displaystyle F\colon \mathbb {R} \to \mathbb {R} }$ der Zahlengerade mit

${\displaystyle F(x+m)=F(x)+m}$

für jede reelle Zahl ${\displaystyle x}$ und jede ganze Zahl ${\displaystyle m}$.

Die Rotationszahl von ${\displaystyle f}$ ist mit Hilfe der Iteration von ${\displaystyle F}$ definiert als:

${\displaystyle \omega (f)=\lim _{n\to \infty }{\frac {F^{n}(x)-x}{n}}}$.

Henri Poincaré bewies, dass der Grenzwert existiert und nicht von der Wahl des Startpunktes ${\displaystyle x}$ abhängt.

Die Hochhebung ${\displaystyle F}$ ist nur modulo ganzzahliger Verschiebungen eindeutig definiert, deshalb ist die Rotationszahl ein wohldefiniertes Element aus ${\displaystyle \mathbb {R} /\mathbb {Z} }$. Anschaulich misst sie den durchschnittlichen Drehwinkel entlang des Orbits von ${\displaystyle f}$.

Beispiele

Drehungen des Kreises

• Wenn ${\displaystyle f=R_{\alpha }}$ die Drehung um den Winkel ${\displaystyle \alpha }$ ist, dann ist ${\displaystyle \omega (f)={\tfrac {1}{2\pi }}\alpha }$.
• Wenn ${\displaystyle f}$ mindestens einen Fixpunkt hat, dann ist ${\displaystyle \omega (f)=0}$. Wenn ${\displaystyle f}$ keine Fixpunkte hat, dann ist ${\displaystyle \omega (f)\not =0}$.
• ${\displaystyle \omega (f)}$ ist rational genau dann, wenn ${\displaystyle f}$ einen periodischen Punkt hat. Wenn ${\displaystyle \omega (f)}$ eine rationale Zahl ${\displaystyle {\tfrac {p}{q}}}$ ist, dann haben alle periodischen Punkte die Periode ${\displaystyle q}$.

Eigenschaften

• Die Rotationszahl ist invariant unter Konjugation: wenn ${\displaystyle h\colon S^{1}\to S^{1}}$ ein Homöomorphismus ist, dann ist ${\displaystyle \omega (hfh^{-1})=\omega (f)}$.
• Die Rotationszahl hängt stetig von ${\displaystyle f}$ ab, d. h. wenn eine Folge ${\displaystyle f_{n}}$ gleichmäßig gegen ${\displaystyle f}$ konvergiert, dann konvergiert ${\displaystyle \omega (f_{n})}$ gegen ${\displaystyle \omega (f)}$.

Anwendungen

• Klassifikationssatz von Poincaré: Wenn ${\displaystyle \omega (f)}$ irrational ist, dann gibt es einen monotone, stetige Abbildung ${\displaystyle h}$ mit

${\displaystyle h\circ f=R_{\omega (f)}\circ h}$,

wobei ${\displaystyle R_{\omega (f)}}$ die Drehung um den Winkel ${\displaystyle \omega (f)}$ bezeichnet. ${\displaystyle h}$ ist ein Homöomorphismus genau dann, wenn die Wirkung von ${\displaystyle f}$ unter Iteration transitiv ist. Beispiele nichttransitiver Homöomorphismen mit irrationaler Rotationszahl wurden von Denjoy konstruiert.

• Wenn ${\displaystyle \omega (f)}$ rational und ${\displaystyle f}$ orientierungserhaltend ist, dann gibt es zwei mögliche Typen periodischer Orbiten:
  • Wenn ${\displaystyle f}$ genau einen periodischen Orbit hat, dann ist jeder andere Punkt unter ${\displaystyle f^{q}}$ heteroklin zu zwei Punkten auf dem periodischen Orbit.
  • Wenn ${\displaystyle f}$ mehrere periodische Orbiten hat, dann ist jeder andere Punkt unter ${\displaystyle f^{q}}$ heteroklin zu zwei Punkten auf unterschiedlichen periodischen Orbiten.

Verallgemeinerungen

Es g​ibt verschiedene Verallgemeinerungen d​er Rotationszahl, d​ie sich (einschließlich Poincarés klassischer Definition) a​lle in d​en folgenden Ansatz einordnen lassen.

Es sei ${\displaystyle G}$ eine lokalkompakte topologische Gruppe und ${\displaystyle \kappa \in {\widehat {H}}_{cb}^{2}(G,\mathbb {Z} )}$ eine beschränkte ${\displaystyle \mathbb {Z} }$-wertige Borel-Kohomologieklasse[1]. Es sei ${\displaystyle g\in G}$. Weil die Einschränkung der entsprechenden reell-wertigen Kohomologieklasse ${\displaystyle \kappa _{\mathbb {R} }\in {\widehat {H}}_{cb}^{2}(G,\mathbb {R} )}$ auf die Untergruppe ${\displaystyle B:={\overline {\langle g\rangle }}\subset G}$ verschwindet, gibt es wegen der exakten Sequenz

${\displaystyle 0\to \operatorname {Hom} _{c}(B,\mathbb {R} /Z)\to {\widehat {H}}_{cb}^{2}(B,\mathbb {Z} )\to {\widehat {H}}_{cb}^{2}(B,\mathbb {R} )\to 0}$

einen eindeutigen stetigen Homomorphismus ${\displaystyle f\colon B\to \mathbb {R} /\mathbb {Z} }$ im Urbild von ${\displaystyle \kappa }$. Die Rotationszahl von ${\displaystyle g}$ wird dann definiert als[2]

${\displaystyle \operatorname {Rot} _{\kappa }(g):=f(g)}$.

• Für ${\displaystyle G=\operatorname {Homeo} ^{+}(S^{1})}$ und ${\displaystyle \kappa =e}$ die Euler-Klasse erhält man die klassische Rotationszahl.[3]
• Für ${\displaystyle G=\operatorname {Sp} (n,\mathbb {R} )}$ und ${\displaystyle \kappa }$ das Bild von ${\displaystyle u(k)=\det(k)^{2}}$ unter ${\displaystyle \operatorname {Hom} _{c}(U(n),\mathbb {R} /Z)\to {\widehat {H}}_{cb}^{2}(U(n),\mathbb {Z} )={\widehat {H}}_{cb}^{2}(\operatorname {Sp} (2n,\mathbb {R} ),\mathbb {Z} )}$ erhält man die symplektische Rotationszahl.[4]
• Für die Automorphismengruppen symmetrischer Gebiete vom Tubentyp erhält man die Clerc-Koufany-Rotationszahl.[5]

Literatur

• Katok, Anatole; Hasselblatt, Boris: Introduction to the modern theory of dynamical systems. With a supplementary chapter by Katok and Leonardo Mendoza. Encyclopedia of Mathematics and its Applications, 54. Cambridge University Press, Cambridge, 1995. ISBN 0-521-34187-6 (Kapitel 11)
• Aranson, S. Kh.; Belitsky, G. R.; Zhuzhoma, E. V.: Introduction to the qualitative theory of dynamical systems on surfaces. Translated from the Russian manuscript by H. H. McFaden. Translations of Mathematical Monographs, 153. American Mathematical Society, Providence, RI, 1996. ISBN 0-8218-0369-7
• Herman, Michael-Robert: Sur la conjugaison différentiable des difféomorphismes du cercle à des rotations. Inst. Hautes Études Sci. Publ. Math. No. 49 (1979), 5–233. doi:10.1007/BF02684798

Weblinks

• Misiurewicz: Rotation theory
• Menon: Circle maps

Einzelnachweise

1. ${\displaystyle {\widehat {H}}_{cb}^{*}(G,\mathbb {Z} )}$ ist die Kohomologie der ${\displaystyle G}$-Invarianten des Komplexes der beschränkten Borel-messbaren Abbildungen ${\displaystyle G^{n+1}\to \mathbb {Z} }$
2. Burger, Marc; Iozzi, Alessandra; Wienhard, Anna: Surface group representations with maximal Toledo invariant. Ann. of Math. (2) 172 (2010), no. 1, 517–566. pdf (Kapitel 7)
3. Ghys, Étienne: Groupes d'homéomorphismes du cercle et cohomologie bornée. The Lefschetz centennial conference, Part III (Mexico City, 1984), 81–106, Contemp. Math., 58, III, Amer. Math. Soc., Providence, RI, 1987.
4. Barge, J.; Ghys, É.: Cocycles d'Euler et de Maslov. Math. Ann. 294 (1992), no. 2, 235–265. pdf
5. Clerc, Jean-Louis; Koufany, Khalid: Primitive du cocycle de Maslov généralisé. Math. Ann. 337 (2007), no. 1, 91–138. pdf