Griolische Präzession

Die Grioli’sche Präzession (nach Giuseppe Grioli) ist in der Kreiseltheorie die reguläre Präzession eines unsymmetrischen, schweren Kreisels.

Grioli’sche Präzession eines Quaders (gelb) mit Hauptachsen (blau), Schwerpunktsachse und Gangpolkegel (rot), Präzessionsachse und Rastpolkegel (grau) sowie Winkelgeschwindigkeit (grün). Bei einem Klotz mit Abmessungen einer Zigarettenschachtel dauert eine Umdrehung etwa ½ Sekunde

Die Bewegungsgleichungen lassen sich geschlossen integrieren, womit diese Bewegung eine der wenigen bekannten räumlichen Lösungen der Euler-Poisson-Gleichungen ist. Grioli zeigte 1947, dass reguläre Präzessionen des unsymmetrischen Kreisels dynamisch möglich sind[1]. M. P. Guljaev führte die Integration der Gleichungen aus[2] und wies nach, dass die gefundene Präzession die einzig mögliche des unsymmetrischen Kreisels ist.[3]

Bewegung des Kreisels

Beschreibung

Bei der regulären Präzession des schweren symmetrischen Lagrange-Kreisels bleiben der Winkel zwischen der Präzessionsachse und der Schwerpunktsachse, die vom Stützpunkt des Kreisels zum Schwerpunkt führt, gleichwie die Winkelgeschwindigkeit und die Präzessionsgeschwindigkeit zeitlich konstant. Diese Charakteristika werden hier auf den schweren unsymmetrischen Kreisel übertragen.

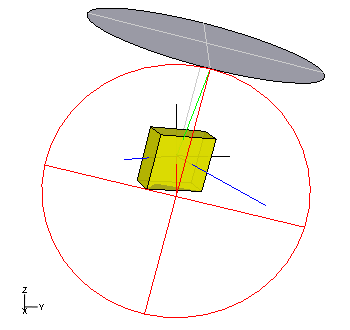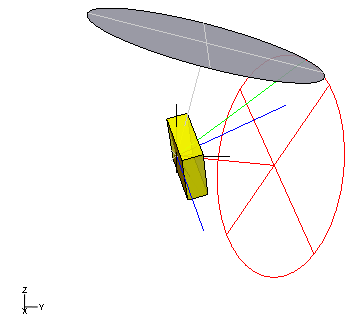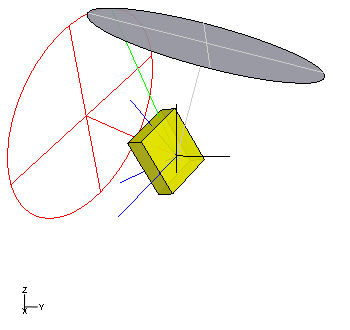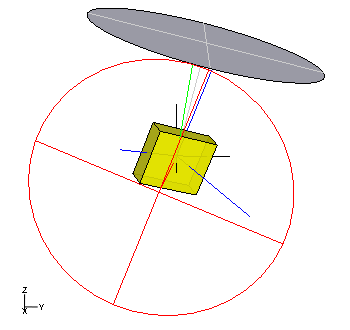
Die Präzessionsachse ist beim unsymmetrischen Kreisel nicht senkrecht. Der Schwerpunkt des Kreisels läuft gleichmäßig in einer raumfesten, zur Präzessionsachse senkrechten Ebene um, die den Stützpunkt enthält und passiert dabei periodisch die Horizontale. Die Hauptachse mit dem mittelgroßen Hauptträgheitsmoment ist senkrecht zur Schwerpunktsachse, umläuft diese mit derselben Drehgeschwindigkeit wie der Schwerpunkt die Präzessionsachse und tritt immer durch diese hindurch, wenn der Schwerpunkt in der Horizontalen ist.

Die Winkelgeschwindigkeit ist die Winkelhalbierende zwischen der Präzessionsachse und der Schwerpunktsachse und besitzt einen konstanten Betrag. Ähnlich wie beim symmetrischen Euler-Kreisel formt die Winkelgeschwindigkeit einen raumfesten Kegel um die Präzessionsachse und im körperfesten System einen Kegel um die Schwerpunktsachse. Die beiden Kegel haben den Öffnungswinkel 45° und rollen gleitungslos aufeinander ab. Die Umsetzung der Lageenergie in Rotationsenergie und umgekehrt geschieht hier ausschließlich durch Rotation um Achsen mit unterschiedlich großen Trägheitsmomenten.

Der Neigungswinkel der Präzessionsachse, die Winkelgeschwindigkeit und die Gesamtenergie des Kreisels sind bei gegebener Massenverteilung im Kreisel festgelegt. Die Ebene senkrecht zur Schwerpunktsachse schneidet das Trägheitsellipsoid des Kreisels in einem Kreis, was Bedingungen an die Massenverteilung im Kreisel stellt.

Die Bewegung kann vollständig mit dem Sinus und Cosinus ausgedrückt werden.

Anfangsbedingungen

Ein Kreisel mit der geforderten Massenverteilung kann wie folgt in reguläre Präzession versetzt werden. Die Schwerpunktsachse muss senkrecht zur Präzessionsachse sein, die den geforderten Winkel mit der Senkrechten einschließt. Die Winkelgeschwindigkeit mit gegebenem Betrag halbiert den Winkel zwischen Präzessions- und Schwerpunktsachse. Die Hauptachsen müssen so ausgerichtet werden, dass sich die geforderte Gesamtenergie des Kreisels ergibt und der Winkel zwischen der Schwerpunktsachse und der Horizontalen, die senkrecht zur Präzessionsachse ist, und der Winkel zwischen der Hauptachse mit dem mittelgroßen Hauptträgheitsmoment und der Präzessionsachse übereinstimmen.

Analytische Formulierung

Im Hauptachsensystem mit 1, 2 bzw. 3-Achsen und zugehörigen Hauptträgheitsmomenten A, B, C, müssen die Schwerpunktskoordinaten s_1,2,3 die Bedingung

s_{2}=0\,\quad {\text{und}}\quad {\frac {s_{3}^{2}}{s_{1}^{2}}}={\frac {B-C}{A-B}}

einhalten. Hier wurde o.B.d.A. A > B > C angenommen. Die raumfeste Standardbasis ê_x,y,z wird so ausgerichtet, dass die Präzessionsachse â keine x-Komponente aufweist:

{\hat {a}}={\begin{pmatrix}0\\\sin(\delta )\\\cos(\delta )\end{pmatrix}}_{{\hat {e}}_{x,y,z}}={\frac {1}{s}}{\begin{pmatrix}s_{3}\sin(\lambda )\\s\cos(\lambda )\\-s_{1}\sin(\lambda )\end{pmatrix}}_{{\hat {e}}_{1,2,3}}

mit dem Neigungswinkel

\tan(\delta )={\frac {\sqrt {(A-B)(B-C)}}{A-B+C}}

der Präzessionsachse gegenüber der Vertikalen ê_z und dem Drehwinkel λ des Kreisels um die Präzessionsachse. Die Schwerpunktsachse mit dem Betrag s läuft gemäß

{\vec {s}}=s{\hat {s}}=s{\begin{pmatrix}\cos(\lambda )\\\cos(\delta )\sin(\lambda )\\-\sin(\delta )\sin(\lambda )\end{pmatrix}}_{{\hat {e}}_{x,y,z}}={\begin{pmatrix}s_{1}\\0\\s_{3}\end{pmatrix}}_{{\hat {e}}_{1,2,3}}

um die Präzessionsachse um. Die Hauptachsen ergeben sich zu

{\begin{array}{lclcl}{\hat {e}}_{1}\!\!\!\!&=&\!\!\!\!{\frac {1}{s}}{\begin{pmatrix}s_{1}\cos(\lambda )-s_{3}\cos(\lambda )\sin(\lambda )\\s_{1}\cos(\delta )\sin(\lambda )+s_{3}[\sin(\delta )\sin(\lambda )+\cos(\delta )\cos ^{2}(\lambda )]\\-s_{1}\sin(\delta )\sin(\lambda )+s_{3}[\cos(\delta )\sin(\lambda )-\sin(\delta )\cos ^{2}(\lambda )]\end{pmatrix}}_{{\hat {e}}_{x,y,z}}\!\!\!\!&=&\!\!\!\!{\begin{pmatrix}1\\0\\0\end{pmatrix}}_{{\hat {e}}_{1,2,3}}\\{\hat {e}}_{2}\!\!\!\!&=&{\begin{pmatrix}\sin ^{2}(\lambda )\\\cos(\lambda )[\sin(\delta )-\cos(\delta )\sin(\lambda )]\\\cos(\lambda )[\cos(\delta )+\sin(\delta )\sin(\lambda )]\end{pmatrix}}_{{\hat {e}}_{x,y,z}}\!\!\!\!&=&\!\!\!\!{\begin{pmatrix}0\\1\\0\end{pmatrix}}_{{\hat {e}}_{1,2,3}}\\{\hat {e}}_{3}\!\!\!\!&=&\!\!\!\!{\frac {1}{s}}{\begin{pmatrix}s_{3}\cos(\lambda )+s_{1}\cos(\lambda )\sin(\lambda )\\s_{3}\cos(\delta )\sin(\lambda )-s_{1}[\sin(\delta )\sin(\lambda )+\cos(\delta )\cos ^{2}(\lambda )]\\-s_{3}\sin(\delta )\sin(\lambda )-s_{1}[\cos(\delta )\sin(\lambda )-\sin(\delta )\cos ^{2}(\lambda )]\end{pmatrix}}_{{\hat {e}}_{x,y,z}}\!\!\!\!&=&\!\!\!\!{\begin{pmatrix}0\\0\\1\end{pmatrix}}_{{\hat {e}}_{1,2,3}}\end{array}}

mit der Winkelgeschwindigkeit

{\vec {\omega }}=\omega _{s}{\begin{pmatrix}\cos(\lambda )\\\sin(\delta )+\cos(\delta )\sin(\lambda )\\\cos(\delta )-\sin(\delta )\sin(\lambda )\end{pmatrix}}_{{\hat {e}}_{x,y,z}}={\frac {\omega _{s}}{s}}{\begin{pmatrix}s_{1}+s_{3}\sin(\lambda )\\s\cos(\lambda )\\s_{3}-s_{1}\sin(\lambda )\end{pmatrix}}_{{\hat {e}}_{1,2,3}}

Der Parameter

\omega _{s}={\frac {\sqrt {2}}{2}}|{\vec {\omega }}|={\sqrt[{4}]{\frac {(mgs)^{2}}{(A-B)(B-C)+(A-B+C)^{2}}}}

ist konstant und gleich der Winkelgeschwindigkeit um die Präzessionsachse und der Schwerpunktsachse.

Es bedeuten

m die Masse,
g die Schwerebeschleunigung,
λ = ω_s t - ε der Drehwinkel,
t die Zeit und
ε ein beliebiger konstanter Phasenwinkel.

Bei λ = nπ, n = 0,1,2,… liegt wegen ê₂ = (−1)ⁿ â die 2-Achse auf der Präzessionsachse. Gleichzeitig passiert wegen ŝ = (−1)ⁿ ê_x die Schwerpunktsachse die x-Achse.

Herleitung

Die Berechnungen benutzen das Hauptachsensystem mit 1-, 2- und 3-Achsen mit Basiseinheitsvektoren ê_1,2,3.

Voraussetzungen

Die Schwerpunktsachse vom Stützpunkt zum Schwerpunkt ist senkrecht auf einem kreisförmigen Schnitt des Trägheitsellipsoids[2][3]:

s_{1}^{2}(B-C)=s_{3}^{2}(A-B),\quad s_{2}=0

vgl. das Hess’sche Pendel, wo die Schnittfigur mit dem MacCullagh-Ellipsoid kreisförmig ist. Von den Identitäten

{\frac {A-B}{s_{1}^{2}}}={\frac {B-C}{s_{3}^{2}}}={\frac {A-C}{s^{2}}}=:k

wird häufig Gebrauch gemacht.

Winkelgeschwindigkeiten

Wie bei der regulären Präzession ist der Betrag der Winkelgeschwindigkeit ${\vec {\omega }}=p{\hat {e}}_{1}+q{\hat {e}}_{2}+r{\hat {e}}_{3}$ und deren Projektion auf die Schwerpunktsachse konstant:

{\begin{array}{lcccccl}\omega ^{2}&=&{\vec {\omega }}\cdot {\vec {\omega }}&=&p^{2}+q^{2}+r^{2}&=&{\text{const.}}\\\omega _{s}&:=&{\dfrac {{\vec {\omega }}\cdot {\vec {s}}}{s}}&=&{\dfrac {s_{1}}{s}}p+{\dfrac {s_{3}}{s}}r&=&{\text{const.}}\end{array}}

Aus den beiden Gleichungen kann r eliminiert und ein funktionaler Zusammenhang

q(p)={\frac {1}{s_{3}}}{\sqrt {-s^{2}p^{2}+2ss_{1}\omega _{s}p+s_{3}^{2}\omega ^{2}-s^{2}\omega _{s}^{2}}}

abgeleitet werden. Die Eulerʹschen Kreiselgleichungen lauten:

{\begin{aligned}A{\dot {p}}&=(B-C)qr-G_{2}s_{3}\\B{\dot {q}}&=(C-A)rp-G_{3}s_{1}+G_{1}s_{3}\\C{\dot {r}}&=(A-B)pq+G_{2}s_{1}\end{aligned}}

Darin sind G_1,2,3 die Komponenten der Gewichtskraft. Multiplikation der ersten Kreiselgleichung mit s₁, der dritten mit s₃ und Addition der resultierenden Gleichungen liefert die Bedingung

s_{1}A{\dot {p}}+s_{3}C{\dot {r}}=(s_{1}p+s_{3}r)ks_{1}s_{3}q=s\omega _{s}ks_{1}s_{3}q

Zeitableitung der Konstanten ω_s ergibt eine weitere Gleichung $s_{1}{\dot {p}}+s_{3}{\dot {r}}=0$ zur Berechnung der Winkelbeschleunigungen mit dem Resultat:

{\dot {p}}={\frac {s_{3}}{s}}\omega _{s}q\quad {\text{und}}\quad {\dot {r}}=-{\frac {s_{1}}{s}}\omega _{s}q

Einsetzen von obigem q(p) ergibt eine autonome Differentialgleichung

{\dot {p}}={\frac {\omega _{s}}{s}}{\sqrt {-s^{2}p^{2}+2ss_{1}\omega _{s}p+s_{3}^{2}\omega ^{2}-s^{2}\omega _{s}^{2}}}

die gelöst werden kann und mit q(p) die gesuchten Winkelgeschwindigkeiten liefern:

{\begin{aligned}p&={\frac {s_{1}}{s}}\omega _{s}+{\frac {s_{3}}{s}}\omega _{\bot }\sin(\omega _{s}t-\varepsilon )\\q&=\omega _{\bot }\cos(\omega _{s}t-\varepsilon )\\r&={\frac {s_{3}}{s}}\omega _{s}-{\frac {s_{1}}{s}}\omega _{\bot }\sin(\omega _{s}t-\varepsilon )\end{aligned}}

Darin ist $\textstyle \omega _{\bot }={\sqrt {\omega ^{2}-\omega _{s}^{2}}}$ , t die Zeit und ε eine Integrationskonstante. Der Übersichtlichkeit halber wird im Folgenden die Abkürzung λ = ω_s t - ε benutzt.

Gewichtskraft

Mit der ersten Kreiselgleichung

{\dot {p}}={\frac {B-C}{A}}qr-{\frac {s_{3}}{A}}G_{2}={\frac {s_{3}}{s}}\omega _{s}q

kann nun die zweite Komponente der Gewichtskraft ausgerechnet werden:

G_{2}={\frac {\omega _{\bot }}{s^{3}}}[\omega _{\bot }(C-A)s_{1}s_{3}\sin(\lambda )\cos(\lambda )-\omega _{s}(As_{1}^{2}+Cs_{3}^{2})\cos(\lambda )]

Sie erfüllt auch die dritte Kreiselgleichung. Die zweite Kreiselgleichung und die konstante Gesamtenergie E liefern zwei Bedingungen

{\begin{aligned}B{\dot {q}}&=(C-A)rp-s_{1}G_{3}+s_{3}G_{1}\\E&={\frac {1}{2}}(Ap^{2}+Bq^{2}+Cr^{2})-s1G_{1}-s_{3}G_{3}\end{aligned}}

für die Ermittlung der Gewichtskräfte in 1- und 3-Richtung:

{\begin{aligned}G_{1}&={\frac {1}{s^{2}}}\left\{s_{1}(E_{\text{rot}}-E)-s_{3}\left[B{\frac {\omega _{s}}{s}}(s_{3}p-s_{1}r)-(A-C)pr\right]\right\}\\G_{3}&={\frac {1}{s^{2}}}\left\{s_{3}(E_{\text{rot}}-E)+s_{1}\left[B{\frac {\omega _{s}}{s}}(s_{3}p-s_{1}r)-(A-C)pr\right]\right\}\end{aligned}}

Darin ist $E_{\text{rot}}={\tfrac {1}{2}}(Ap^{2}+Bq^{2}+Cr^{2})$ die Rotationsenergie. Die Gewichtskraft $\textstyle {\vec {G}}=\sum _{i=1}^{3}G_{i}{\hat {e}}_{i}$ ist konstant, womit ihre Zeitableitung verschwindet:

{\displaystyle {\dot {\vec {G}}}=\sum _{i=1}^{3}{\dot {G}}_{i}{\hat {e}}_{i}+\sum _{i=1}^{3}G_{i}{\dot {\hat {e}}}_{i}{\stackrel {\displaystyle

Die Zeitableitungen der Basisvektoren berechnen sich mit der Winkelgeschwindigkeit gemäß ${\dot {\hat {e}}}_{i}={\vec {\omega }}\times {\hat {e}}_{i}$ , was die Konsequenz

\sum _{i=1}^{3}{\dot {G}}_{i}{\hat {e}}_{i}+\sum _{i=1}^{3}G_{i}{\vec {\omega }}\times {\hat {e}}_{i}={\vec {0}}\quad {\text{oder}}\quad {\begin{pmatrix}{\dot {G}}_{1}\\{\dot {G}}_{2}\\{\dot {G}}_{3}\end{pmatrix}}_{{\hat {e}}_{1,2,3}}={\begin{pmatrix}rG_{2}-qG_{3}\\pG_{3}-rG_{1}\\qG_{1}-pG_{2}\end{pmatrix}}_{{\hat {e}}_{1,2,3}}

hat. Einsetzen obiger Komponenten G_1,2,3 zeigt, dass ω_⊥ = ω_s und somit ω = √2 ω_s ist. Außerdem gibt es für die Gesamtenergie nur einen möglichen Wert.

Energien

Die Energien des Kreisels ergeben sich zu

{\begin{aligned}E&={\frac {A+C}{2}}\omega _{s}^{2}=E_{\text{rot}}+E_{\text{pot}}\\E_{\text{rot}}&=\omega _{s}^{2}\left[{\frac {A+C}{2}}+(A-C){\frac {s_{1}s_{3}}{s^{2}}}\sin(\lambda )\right]\\E_{\text{pot}}&=-\omega _{s}^{2}(A-C){\frac {s_{1}s_{3}}{s^{2}}}\sin(\lambda )\end{aligned}}

Die Lageenergie schwingt um den Nullpunkt auf Höhe des Stützpunkts und die Rotationsenergie gegenläufig um den konstanten Mittelwert E.

Präzessionsgeschwindigkeit

Die Gleichungen haben noch zwei freie Parameter ω_s und ε, von denen letzterer beliebig ist. Sei λ = 0. Dann lautet die Gewichtskraft im Hauptachsensystem

{\vec {G}}(\lambda =0)={\frac {\omega _{s}^{2}}{s^{3}}}[(B-C)s_{1}s{\hat {e}}_{1}-(As_{1}^{2}+Cs_{3}^{2}){\hat {e}}_{2}-(A-B)s_{3}s{\hat {e}}_{3}]

Sie hat den Betrag m g mit der Masse m und der Schwerebeschleunigung g, was die Winkelgeschwindigkeit

\omega _{s}={\sqrt[{4}]{\frac {(mgs)^{2}}{(A-B)(B-C)+(A-B+C)^{2}}}}

um die Schwerpunktsachse und die Präzessionsachse festlegt.

Präzessionsachse

Bei einer regulären Präzession rotiert die Drehachse um eine raumfeste Achse, die Präzessionsachse â. Deren Zeitableitung muss verschwinden, so dass analog zur Gewichtskraft oben für die Komponenten a_1,2,3

{\begin{pmatrix}{\dot {a}}_{1}\\{\dot {a}}_{2}\\{\dot {a}}_{3}\end{pmatrix}}_{{\hat {e}}_{1,2,3}}={\begin{pmatrix}ra_{2}-qa_{3}\\pa_{3}-ra_{1}\\qa_{1}-pa_{2}\end{pmatrix}}_{{\hat {e}}_{1,2,3}}

gelten muss. Die Achse

{\hat {a}}={\begin{pmatrix}{\frac {s_{3}}{s}}\sin(\lambda )\\\cos(\lambda )\\-{\frac {s_{1}}{s}}\sin(\lambda )\end{pmatrix}}_{{\hat {e}}_{1,2,3}}

erfüllt mit λ = ω_s t - ε diese Bedingung. Aus dem Skalarprodukt mit der lotrechten Gewichtskraft

{\frac {{\hat {a}}\cdot (-{\vec {G}})}{mg}}=\cos(\delta )={\sqrt {\frac {(A-B+C)^{2}}{(A-B)(B-C)+(A-B+C)^{2}}}}

ermittelt sich der Neigungswinkel δ der Präzessionsachse gegenüber der Vertikalen. Wegen

{\hat {a}}\cdot {\vec {s}}=0\quad {\text{und}}\quad {\frac {{\hat {a}}\cdot {\vec {\omega }}}{\omega }}={\frac {{\vec {s}}\cdot {\vec {\omega }}}{s\omega }}=\cos 45^{\circ }

halbiert die Winkelgeschwindigkeit jederzeit den rechten Winkel zwischen der Präzessions- und der Schwerpunktsachse. Die Skalarprodukte ${\hat {a}}\cdot {\vec {\omega }}={\frac {1}{s}}{\vec {s}}\cdot {\vec {\omega }}=\omega _{s}$ zeigen, dass die Drehgeschwindigkeiten um die Präzessionsachse und um die Schwerpunktsachse beide gleich dem Parameter ω_s sind.

Hauptachsen

Die Schwerpunktsachse führt eine Kreisbewegung um die Präzessionsachse â aus und passiert dabei periodisch die x-Achse. Das raumfeste Basissystem {ê_x, ê_b = â × ê_x, â} wird für die Darstellung

ŝ = cos( λ ) ê_x + sin( λ ) ê_b

der Schwerpunktsachse benutzt, wo ŝ der Einheitsvektor in deren Richtung ist. Um diese kreist der Körper, was mit den Basisvektoren {ŝ, ĥ = â × ŝ, â} beschrieben werden kann. Die Basisvektoren

î = sin( λ ) â + cos( λ ) ĥ

ĵ = cos( λ ) â - sin( λ ) ĥ

rotieren wie gefordert um ŝ. Die zweite Hauptachse ist senkrecht zur Schwerpunktsachse und liegt bei λ = 0 auf der Präzessionsachse, was ê₂ = ĵ impliziert. Die beiden anderen Hauptachsen ergeben sich aus

s ŝ = s₁ ê₁ + s₃ ê₃

s ê₂ × ŝ = s î = s₃ ê₁ - s₁ ê₃

in der im Abschnitt #Analytische Formulierung angegebenen Form.

Symmetrische Kreisel

Die Herleitung und die Formeln sind auch für den schweren symmetrischen Kreisel mit A = B gültig. Dann ist s₁ = s₂ = 0 und s₃ = s, sodass der Schwerpunkt auf der Symmetrie- oder Figurenachse liegt. Die Präzessionsachse â ist wegen tan( δ ) = 0 lotrecht und die dazu senkrechte Schwerpunkts- und Figurenachse ist horizontal. Die Winkelgeschwindigkeit überstreicht wegen

{\vec {\omega }}=\omega _{s}{\begin{pmatrix}\cos(\lambda )\\\sin(\lambda )\\1\end{pmatrix}}_{{\hat {e}}_{x,y,z}}=\omega _{s}{\begin{pmatrix}\sin(\lambda )\\\cos(\lambda )\\1\end{pmatrix}}_{{\hat {e}}_{1,2,3}}\quad {\text{mit}}\quad \omega _{s}={\frac {\sqrt {2}}{2}}|{\vec {\omega }}|={\sqrt {\frac {mgs}{C}}}

sowohl um die z-Achse als auch um die Figurenachse einen Kegel mit dem Öffnungswinkel 45°. Dieser Spezialfall ist demnach die reguläre Präzession eines Lagrange-Kreisels mit horizontaler Figurenachse bei Gleichheit der Präzessionsgeschwindigkeit und der Eigendrehgeschwindigkeit um die 3-Achse. Mit dem Drehimpuls

{\vec {L}}=\omega _{s}{\begin{pmatrix}C\cos(\lambda )\\C\sin(\lambda )\\A\end{pmatrix}}_{{\hat {e}}_{x,y,z}}=\omega _{s}{\begin{pmatrix}A\sin(\lambda )\\A\cos(\lambda )\\C\end{pmatrix}}_{{\hat {e}}_{1,2,3}}

wird die Bedingung

L_z · L₃ = Amgs

für die reguläre Präzession mit horizontaler Figurenachse erfüllt.

Bei B = C ergibt sich eine analoge Bewegung mit der 1-Achse als Figurenachse.

Der Fall von Harlamowa

E. I. Harlamowa konstruierte eine Lösung der Kreiselgleichungen, die die einzige, dynamisch mögliche Präzession eines unsymmetrischen Kreisels um eine vertikale Achse darstellt. Die Präzessionsgeschwindigkeit ist dort nicht konstant und die Hauptträgheitsmomente müssen die Bedingung C > 2A > 2B einhalten. Die Lösung beschreibt deshalb keinen starren Körper, denn bei dem ist A + B > C. M. P. Guljaev bemerkte, dass ein starrer Körper mit Hohlräumen, die mit einer inkompressiblen idealen Flüssigkeit gefüllt sind, die Bedingung einhalten kann.[Anmerkung 1]

Anmerkungen:

Leimanis (1965), S. 116.

Literatur

Giuseppe Grioli: Existenz und Bestimmung von regelmäßigen, dynamisch möglichen Präzessionsbewegungen eines asymmetrischen schweren Körpers. In: Annali di Matematica Pura ed Applicata. Band 26, Nr. 1. Swets & Zeitlinger, 1947, ISSN 0373-3114, S. 271–281, doi:10.1007/BF02415381 (italienisch, Originaltitel: Esistenza e determinazione delle precessioni regolari dinamicamente possibili per un solido pesante asimmetrico.).
Eugene Leimanis: The General Problem of the Motion of Coupled Rigid Bodies about a Fixed Point. Springer Verlag, Berlin, Heidelberg 1965, ISBN 978-3-642-88414-6, S. 109 ff., doi:10.1007/978-3-642-88412-2 (englisch, eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 21. März 2018]).
K. Magnus: Kreisel: Theorie und Anwendungen. Springer, 1971, ISBN 978-3-642-52163-8, S. 143 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 20. Februar 2018]).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[4] Leimanis (1965), S. 116.

[1] Giuseppe Grioli: Existenz und Bestimmung von regelmäßigen, dynamisch möglichen Präzessionsbewegungen eines asymmetrischen schweren Körpers. In: Annali di Matematica Pura ed Applicata. Band 26, Nr. 1. Swets & Zeitlinger, 1947, ISSN 0373-3114, S. 271–281, doi:10.1007/BF02415381 (italienisch, Originaltitel: Esistenza e determinazione delle precessioni regolari dinamicamente possibili per un solido pesante asimmetrico.).

[leimanis-2] Eugene Leimanis: The General Problem of the Motion of Coupled Rigid Bodies about a Fixed Point. Springer Verlag, Berlin, Heidelberg 1965, ISBN 978-3-642-88414-6, S. 109 ff., doi:10.1007/978-3-642-88412-2 (englisch, eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 21. März 2018]).

[magnus-3] K. Magnus: Kreisel: Theorie und Anwendungen. Springer, 1971, ISBN 978-3-642-52163-8, S. 143 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 20. Februar 2018]).