Gorjatschew-Tschaplygin-Kreisel

Der Gorjatschew-Tschaplygin-Kreisel[1] (englisch Goryachev-Chaplygin top) nach Dmitri Nikanorowitsch Gorjatschew und Sergei Alexejewitsch Tschaplygin ist in der Kreiseltheorie einer der wenigen Fälle, bei denen sich die Euler’schen Kreiselgleichungen analytisch lösen lassen. Die drei Hauptträgheitsmomente A, B und C des schweren Kreisels erfüllen die Bedingung A = B = 4C und der Schwerpunkt liegt in der von den zu A und B gehörenden Hauptachsen aufgespannten Ebene. Der Kreisel ist somit eine Abwandlung des Kowalewskaja-Kreisels.

Die Zeitintegration der Kreiselgleichungen ist möglich, weil es neben der Gesamtenergie und dem Drehimpuls L_z in Lotrichtung eine dritte kinetische Erhaltungsgröße f gibt, siehe #Integrale der Bewegung, die jedoch nur dann konstant ist, wenn L_z anfänglich verschwindet. Wie beim Kowalewskaja-Kreisel sind die Lösungen hyper- oder ultraelliptische Funktionen aber die Komplexität des #Bifurkationsdiagramms erreicht nicht diejenige von Kowalewskajas Fall. Charakteristisch für den Gorjatschew-Tschaplygin-Kreisel sind (quasi-)periodische #Pendelbewegungen, bei denen f = 0 ist[2].

Gorjatschew diskutierte 1899 genau diese Bewegungen[3] und Tschaplygin konnte 1901 die allgemeine Lösung der Bewegungsgleichungen angeben[4].

Phänomenologie

Pendelbewegungen

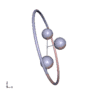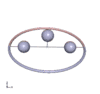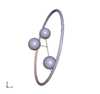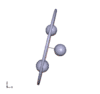Abb. 1
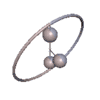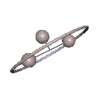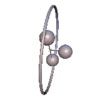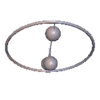Abb. 2

Charakteristisch für den Gorjatschew-Tschaplygin-Kreisel sind Pendelbewegungen, bei denen das Integral f verschwindet. Das ist jedenfalls dann der Fall, wenn der Kreisel um seine 2- oder 3-Achse periodisch pendelt, wobei auch Überschläge stattfinden können, sodass der Kreisel ins Rotieren kommt. Andere Bewegungen mit f = 0 sind räumliche Pendelbewegungen, s. Animationen.

Bifurkationsdiagramm

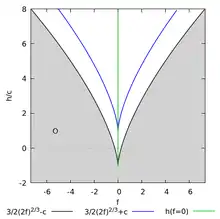
Abb. 3: Bifurkationsdiagramm des Gorjatschew-Tschaplygin-Kreisels

Bifurkation (Verzweigung) ist das Phänomen, das ein System an einem kritischen Punkt in verschiedene Zustände verzweigen kann. So kann ein lotrecht stehender Stab bei kleiner Störung nach links oder rechts umfallen sofern er irgendwie an eine Ebene gebunden ist. Die Trennlinie zwischen den beiden Pfaden ist eine Separatrix, von der auch beim unsymmetrischen Euler-Kreisel eine existiert. Die Bewegungen entlang der Separatrizen sind oft instabil. Das Bifurkationsdiagramm des Gorjatschew-Tschaplygin-Kreisels hat nur eine Separatrix (blau im Bild) und ist damit weniger komplex als das des Kowalewskaja-Kreisels.

Die kritischen Punkte beim Gorjatschew-Tschaplygin-Kreisel stellen sich bei bestimmten Werten der Gesamtenergie h und des Integrals f ein, siehe #Integrale der Bewegung. Das Bifurkationsdiagramm besteht aus zwei Flächen, wobei in der grauen Fläche O Parameterkombinationen auftreten, die dem Kreisel bei L_z = 0 verwehrt sind. Die weißen Bereiche sind dem Kreisel zugänglich. Auf der Ordinate mit f = 0 finden oben beschriebene Pendelbewegungen statt.

Der schwarze Rand des unzugänglichen Gebiets O definiert einen Kreisel, der periodisch durch den unteren Totpunkt schwingt oder rotiert, je nachdem h < c oder h > c, siehe den folgenden Abschnitt.

Bewegungen mit minimaler Energie

Abb. 4: Bewegung bei gegebenem f und minimaler Energie

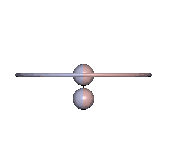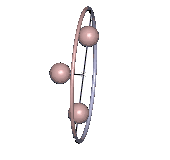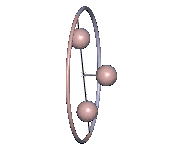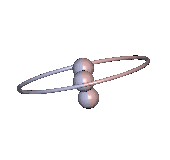
Die Bedingung, dass der Drehimpuls L_z in Lotrichtung verschwinde, schränkt die Bewegungsmöglichkeiten des Kreisels ein. Es können auch Rotationen mit L_z ≠ 0 auftreten, aber die werden hier nicht betrachtet. Gleichmäßige Drehungen um eine vertikale Hauptachse, wie sie beim Lagrange-Kreisel und dem Kowalewskaja-Kreisel vorkommen, sind damit ausgeschlossen. Wenn eine Hauptachse irgendwann senkrecht steht, dann muss hier in dem Moment die Drehachse senkrecht zu ihr sein. Ein Beispiel für eine solche Bewegung mit minimaler Energie ist in Abb. 4 zu sehen.

Bewegungen auf der Separatrix

Abb. 5: Bewegung auf der Separatrix

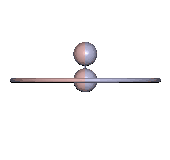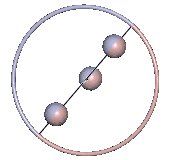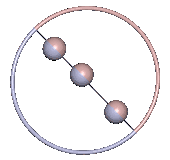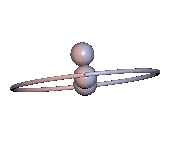
Auf der Separatrix bewegt sich die 1-Achse durch den oberen Totpunkt und wie bei den Bewegungen mit minimaler Energie oben muss zu dem Zeitpunkt die Drehachse senkrecht zur 1-Achse sein, siehe Abb. 5. Die Bewegung auf der Separatrix ist instabil.

Pseudoreguläre Präzession

Wenn die Winkelgeschwindigkeit um die Schwerpunktsachse vom Stützpunkt zum Schwerpunkt sehr groß ist, dann bewegt sich der Kreisel analog zur pseudoregulären Präzession des Lagrange-Kreisels[4].

Lösung der Bewegungsgleichungen

Euler-Poisson-Gleichungen

Aus Symmetriegründen kann die zu A gehörende erste Hauptträgheitsachse so gewählt werden, dass der Schwerpunkt des Kreisels auf ihr liegt. Damit spezialisieren sich die Euler-Poisson-Gleichungen beim Gorjatschew-Tschaplygin-Kreisel zu[5]

{\begin{aligned}4{\dot {p}}=&3qr\\4{\dot {q}}=&-3pr+cn_{3}\\{\dot {r}}=&-cn_{2}\\{\dot {n}}_{1}=&rn_{2}-qn_{3}\\{\dot {n}}_{2}=&pn_{3}-rn_{1}\\{\dot {n}}_{3}=&qn_{1}-pn_{2}\end{aligned}}

Darin sind im Hauptachsensystem

p, q, r = ω_1,2,3 die Komponenten der Winkelgeschwindigkeit,
n_1,2,3 die Komponenten des zur Gewichtskraft antiparallel nach oben weisenden Einheitsvektors,
$c={\tfrac {mgs_{1}}{C}}$ $\text{[math]}$ ein Parameter mit der Dimension T⁻², der die Wirkung der Gewichtskraft zusammenfasst,
- m die Masse des Kreisels,
- g die Schwerebeschleunigung und
- s₁ der Abstand des Schwerpunkts vom Stützpunkt.

Wie beim Kowalewskaja-Kreisel entstehen durch Skalierung der Zeit mit √c und der Winkelgeschwindigkeiten mit √c⁻¹ Bewegungsgleichungen mit c = 1, sodass sie keinen freien Parameter mehr besitzen. Mathematisch reicht es aus, nur diesen Fall c = 1 zu betrachten.

Integrale der Bewegung

Wie bei jedem schweren Kreisel ist die Norm des Richtungsvektors der Gewichtskraft $|{\hat {n}}|$ , der Drehimpuls ${\vec {L}}$ in Lotrichtung und die Gesamtenergie E konstant:[6]

{\begin{aligned}{\hat {n}}\cdot {\hat {n}}=&n_{1}^{2}+n_{2}^{2}+n_{3}^{2}=1={\text{const.}}\\l:=&{\frac {{\vec {L}}\cdot {\hat {n}}}{C}}=4pn_{1}+4qn_{2}+rn_{3}={\text{const.}}\\h:=&{\frac {E}{C}}=2(p^{2}+q^{2})+{\frac {1}{2}}r^{2}+c\,n_{1}={\text{const.}}\end{aligned}}

Diese Konstanten werden in der Kreiseltheorie Integrale genannt, die ersten beiden auch Casimir-Invarianten. Die Gesamtenergie wird in der analytischen Mechanik auch als Hamilton-Funktion bezeichnet, was ihre Benennung mit h begründet. Beim Gorjatschew-Tschaplygin-Kreisel verschwindet l nach Voraussetzung und dann gibt es noch ein viertes rationales Integral[7]

f=(p^{2}+q^{2})r-cpn_{3}

Denn nach den #Euler-Poisson-Gleichungen und der Produktregel erweist sich die Zeitableitung

{\dot {f}}=(2p{\dot {p}}+2q{\dot {q}})r+(p^{2}+q^{2}){\dot {r}}-c{\dot {p}}n_{3}-cp{\dot {n}}_{3}=-{\frac {cq}{4}}l

als proportional zum lotrechten Impuls, der nach Voraussetzung null ist.

Wenn f = 0 ist, dann existiert ein weiteres Integral

a^{n}={\frac {p^{2}+q^{2}}{\sqrt[{3}]{p^{2}}}}

denn die Zeitableitung erweist sich nach der Quotientenregel in Kombination mit den #Euler-Poisson-Gleichungen als proportional zu f:

na^{n-1}{\dot {a}}={\frac {(2p{\dot {p}}+2q{\dot {q}})p^{\frac {2}{3}}-(p^{2}+q^{2}){\frac {2}{3}}p^{-{\frac {1}{3}}}{\dot {p}}}{p^{\frac {4}{3}}}}=-{\frac {q}{2p^{\frac {5}{3}}}}f

Gorjatschew benutzte n = ⁴⁄₃, womit a die Dimension einer Winkelgeschwindigkeit bekommt, es wird aber auch n = 1 benutzt[8].

Gleichgewichtslösungen

Die Bedingung, dass der Drehimpuls l in Lotrichtung verschwinde, schränkt die Bewegungsmöglichkeiten des Kreisels ein. Es können auch Rotationen mit l ≠ 0 auftreten, aber die werden hier nicht betrachtet. Wenn eine Hauptachse irgendwann senkrecht ist, dann muss hier in dem Moment die Drehachse senkrecht zu ihr sein.

Relative Gleichgewichte sind Fixpunkte der #Euler-Poisson-Gleichungen, die bei Konstanz aller Größen auftreten. Wird die Bedingung l = 0 angenommen, gibt es keine vom Stillstand abweichenden Gleichgewichte.

Denn aus der dritten Euler-Poisson-Gleichung folgt n₂ = 0 und aus der sechsten n₁ q = 0, wo zwei Fälle zu unterscheiden sind.

Falls n₁ = 0 ist n₃ = ±1 und aus der vierten und fünften Euler-Poisson-Gleichung ergibt sich p = q = 0. Das ist aber im Widerspruch zur zweiten Gleichung. Also muss n₁ ≠ 0 sein.
Falls q = 0, ist wegen der fünften Gleichung r = n₃ p / n₁ und l = 0 erzwingt p = r = 0.

Ohne die Bedingung l = 0 stellen sich zum Kowalewskaja-Kreisel analoge Gleichgewichte ein. Die Rotation um die vertikale 1-Achse ist stabil, wenn der Schwerpunkt unterhalb des Stützpunkts ist, und instabil, wenn er sich darüber befindet[9].

Bewegungen mit minimaler Energie

Auf dem schwarzen Rand des dem Kreisel zugänglichen Gebiets im #Bifurkationsdiagramm läuft die 1-Achse des Kreisels durch den unteren Totpunkt. Für beliebiges f ∈ ℝ ist die Gesamtenergie

\textstyle h={\tfrac {3}{2}}{\sqrt[{3}]{(2f)^{2}}}-c

und im unteren Totpunkt ergibt sich

{\begin{aligned}h=&2q^{2}+{\frac {1}{2}}r^{2}-c,&f=&q^{2}r\\n_{1}=&-1,&n_{2}&=n_{3}=0\\p=&0,&q=&{\sqrt[{3}]{\frac {2f}{\sqrt {8}}}},&r=&{\sqrt[{3}]{2f}}\end{aligned}}

Auf der Separatrix läuft der Kreisel durch den oberen Totpunkt, sodass dort abweichend

n_{1}=1\quad {\text{und}}\quad h=2q^{2}+{\frac {1}{2}}r^{2}+c={\frac {3}{2}}{\sqrt[{3}]{(2f)^{2}}}+c

vorliegt.

Gorjatschews Ausarbeitung

Gorjatschew ging in seiner Ausarbeitung[3] vom Integral a aus und zeigte in seinen Gleichungen (7) und (8), dass dieses existiert, wenn die #Integrale der Bewegung f und l null sind. Mit Hilfe dieser Konstanten ermittelte er die Fläche, die von der Winkelgeschwindigkeit im körperfesten Bezugssystem erzeugt wird. Dazu eliminierte er mit Hilfe der Integrale h, f und l die Richtungskosinus n_1,2,3, und die Summe deren Quadrate, die gleich eins ist, führt auf seine Gleichung (13):

( a⁴r² + 8a⁴ρ² - 2hρ⁴ )² = λρ⁴( a⁴ - ρ⁴ )

Darin ist ρ² = p² + q² und λ = 4( 16a⁴ + 4c² - h² ) eine Konstante der Bewegung. Diese Gleichung gibt r als Funktion von ρ. Durch das Integral a ist außerdem

p² = ρ⁶/a⁴

q² = ρ²(a⁴-ρ⁴)/a⁴

sodass sich die Winkelgeschwindigkeit vollständig als Funktion von ρ darstellt. Bei der Eliminierung der Richtungskosinus entstanden Identitäten, die auch die n_1,2,3 auf ρ zurück führen. Damit liegt die mit ρ parametrisierte Trajektorie des Kreisels im körperfesten Bezugssystem fest.

Tschaplygins Lösung

Tschaplygin gelang es die Lösungsfunktionen auf ein System von Abel-Jacobi Gleichungen zu reduzieren[10]. Dazu werden Variablen u und v eingeführt:

4( p² + q² ) = uv und r = u - v

Mit den Abkürzungen

{\begin{array}{lcllcl}U&=&u^{3}-2hu-4f,&V&=&v^{3}-2hv+4f\\U_{1}^{2}&=&U-2cu,&V_{1}^{2}&=&V-2cv\\-U_{2}^{2}&=&U+2cu,&-V_{2}^{2}&=&V+2cv\end{array}}

können alle Zustandsgrößen mittels

{\begin{array}{lcllcl}8cp&=&U_{1}V_{2}-U_{2}V_{1},&2cn_{1}&=&-{\frac {U+V}{u+v}}\\8cq&=&U_{1}V_{1}+U_{2}V_{2},&2cn_{2}&=&-{\frac {U_{1}U_{2}-V_{1}V_{2}}{u+v}}\\r&=&u-v,&2cn_{3}&=&-{\frac {U_{1}V_{2}+U_{2}V_{1}}{u+v}}\end{array}}

und die Zeitableitungen

{\frac {\mathrm {d} u}{\mathrm {d} t}}={\frac {U_{1}U_{2}}{2(u+v)}}\quad {\text{und}}\quad {\frac {\mathrm {d} v}{\mathrm {d} t}}={\frac {V_{1}V_{2}}{2(u+v)}}

dargestellt werden. Daher ist

{\frac {\mathrm {d} u}{U_{1}U_{2}}}-{\frac {\mathrm {d} v}{V_{1}V_{2}}}=0\quad {\text{und}}\quad {\frac {2u\,\mathrm {d} u}{U_{1}U_{2}}}+{\frac {2v\,\mathrm {d} v}{V_{1}V_{2}}}=\mathrm {d} t

und das Problem ist auf hyperelliptische Integrale zurückgeführt[6].

Andoyer–Deprit Variablen L und G sind mit u und v über L = u - v und G = u + v verbunden[10].

Fußnoten

Gorjatschew (1899), Magnus (1971), Leimanis (1965), Borisov u. Mamaev (2001), siehe Literatur.
Borisov, Mamaev (2001), S. 271.
Gorjatschew (1899), siehe Literatur.
Leimanis (1965), S. 92.
Magnus (1971), S. 130, und Leimanis (1965), S. 92.
Leimanis (1965), S. 93.
Magnus (1971), S. 130, Leimanis (1965), S. 93, Borisov u. Mamaev (2001), S. 269. Dort ist γ_1,2,3 = -n_1,2,3.
Borisov u. Mamaev, S. 271, Leimanis (1965), S. 94, Gorjatschew (1899), S. 433.
Leimanis (1965), S. 95.
Borisov u. Mamaev (2001), S. 269.

Literatur

D. N. Gorjatschew: Über die Bewegung eines schweren starren Körpers um einen Fixpunkt im Fall A = B = 4C. 1899 (russisch, mathnet.ru – Originaltitel: 0 движеніи тяжелаго твердаго тѣла вокругъ неподвижной точки в ъ случаѣ А = В = 4C.).
K. Magnus: Kreisel: Theorie und Anwendungen. Springer, 1971, ISBN 978-3-642-52163-8, S. 129 ff. (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 20. Februar 2018]).
A. V. Borisov, I. S. Mamaev: Euler-Poisson Equations and Integrable Cases. 2001, S. 269 ff., doi:10.1070/RD2001v006n03ABEH000176, arxiv:nlin/0502030 (englisch, Enthält Lösungen der Kreiselgleichungen, deren ausführliche Beschreibung und weiter führende Literaturangaben.).
Eugene Leimanis: The General Problem of the Motion of Coupled Rigid Bodies about a Fixed Point. Springer Verlag, Berlin, Heidelberg 1965, ISBN 978-3-642-88414-6, S. 92 ff., doi:10.1007/978-3-642-88412-2 (englisch, eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 21. März 2018]).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Gorjatschew (1899), Magnus (1971), Leimanis (1965), Borisov u. Mamaev (2001), siehe Literatur.

[2] Borisov, Mamaev (2001), S. 271.

[gorjatschew-3] Gorjatschew (1899), siehe Literatur.

[leimanis92-4] Leimanis (1965), S. 92.

[5] Magnus (1971), S. 130, und Leimanis (1965), S. 92.

[leimanis93-6] Leimanis (1965), S. 93.

[7] Magnus (1971), S. 130, Leimanis (1965), S. 93, Borisov u. Mamaev (2001), S. 269. Dort ist γ_1,2,3 = -n_1,2,3.

[8] Borisov u. Mamaev, S. 271, Leimanis (1965), S. 94, Gorjatschew (1899), S. 433.

[9] Leimanis (1965), S. 95.

[borisov269-10] Borisov u. Mamaev (2001), S. 269.