Oval
Der Begriff Oval (lateinisch ovum ‚Ei‘) bezeichnet eine ebene rundliche konvexe Figur, die im weitesten Sinne dem Profil eines Vogeleis ähnelt. Sie umfasst Kreise und Ellipsen als Spezialfälle, wobei ein beliebiges Oval im Gegensatz zu diesen keine Symmetrieachse besitzen muss.
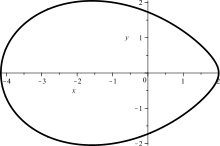
Die Verwendung des Begriffs ist nicht immer ganz einheitlich, gelegentlich wird er auch rein beschreibend verwandt. In der Analysis lässt er sich jedoch formal mit Hilfe ebener Kurven definieren, in diesem Zusammenhang spricht man dann auch von Eikurven oder Eilinien.
Ein dreidimensionaler rundlicher konvexer Körper (allgemeiner auch eine abgeschlossene konvexe Teilmenge des ) wird als Ovoid bezeichnet.[1] In diesem Sinne ist ein Oval mit seinem Inneren dann ein zweidimensionales Ovoid.
In der projektiven Geometrie werden die Begriffe Oval und Ovoid ohne Differenzierbarkeits- und Konvexitätsbedingungen ausschließlich mit Hilfe von Inzidenzbedingungen („Jede Gerade trifft ein Oval bzw. Ovoid in höchstens 2 Punkten“) als quadratische Mengen definiert. Ein Oval, wie es im vorliegenden Artikel erläutert wird, ist im projektiven Abschluss der reellen Ebene stets ein Oval im Sinne der projektiven Definition, falls man zusätzlich verlangt, dass die Krümmung des Ovals auf keinem Abschnitt verschwindet. Ein solches Oval ist dann der Rand einer streng konvexen Menge, d. h., es enthält keine Geradenstücke.
Formale Definition und Eigenschaften
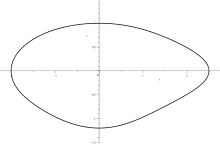
Die rundliche Form eines Ovals erhält man, indem man für eine geschlossene Kurve Glattheit und Konvexität verlangt. Dies führt dann zu der folgenden Definition:
- Eine geschlossene zweimal stetig differenzierbare konvexe Kurve in der Ebene heißt Oval (auch Eikurve oder Eilinie).[2][3][4]
Diese Definition erfasst jedoch nicht alle geometrischen Figuren, die gelegentlich als Ovale bezeichnet werden. So erfüllen zum Beispiel Ovale, die aus unterschiedlichen Kreisbögen zusammengesetzt sind, diese Definition nicht, da ihre zweite Ableitung nicht auf der gesamten Kurve stetig ist. Möchte man auch solche Fälle erfassen, so muss man Abstriche an die Glattheit der Kurve machen (Differentiationsklasse oder statt ). Gelegentlich wird daher auch nur die Konvexität gefordert.[5][6] Dies hat jedoch den Nachteil, dass die Definition dann auch Figuren umfasst, die man normalerweise kaum als "eiförmig" empfindet wie zum Beispiel konvexe Polygone.
Ein Oval im Sinne der obigen Definition besitzt die folgenden Eigenschaften:
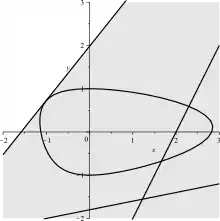
- Ein Oval ist eine Jordan-Kurve, d. h., es besitzt keine Schlingen oder Schlaufen.
- Die orientierte Krümmung eines Ovals besitzt keinen Vorzeichenwechsel, d. h., je nach Durchlaufsinn ist die orientierte Krümmung für jeden Punkt des Ovals entweder nichtnegativ oder nichtpositiv. Anschaulich bedeutet dies, dass es keine Wendungen oder Einbuchtungen besitzt. Man kann es nur in einer reinen Linkskurve bzw. Rechtskurve durchlaufen.
- Das Innere eines Ovals ist eine konvexe Menge, und das Oval bildet deren Rand.
- Für Ovale gilt der Vierscheitelsatz, das heißt, die Krümmung eines Ovals besitzt mindestens vier Extremstellen.[7]
- Besitzt ein Punkt des Ovals eine Tangente, so befindet sich das gesamte Oval auf einer Seite der Tangente.
- Verlangt man zusätzlich, dass die Krümmung des Ovals auf keinem Abschnitt verschwindet, das heißt, die Krümmung nimmt höchstens in isolierten Punkten den Wert Null an, dann existiert in jedem Punkt des Ovals die obige Tangente. Allgemeiner gilt dann für eine beliebige Gerade, dass sie mit dem Oval entweder keinen Punkt (Passante), genau einen Punkt (Tangente) oder genau zwei Punkte (Sekante) gemeinsam hat.
Beispiele und Konstruktionen
Ovale können mit völlig unterschiedlichen Verfahren konstruiert werden. Eine Reihe von Konstruktionsverfahren erhält man aus den verschiedenen Konstruktionsverfahren für Ellipsen, die man jeweils an einer geeigneten Stelle leicht modifiziert.
Man kann eine Ellipse erzeugen, indem man einen Kegel mit einer Ebene schneidet (siehe Kegelschnitte). Verwendet man nun statt des Kegels bestimmte andere Rotationskörper, beispielsweise eine rotierte Hyperbel, so erhält man bei einem Schnitt mit einer Ebene auch von Ellipsen verschiedene Ovale. Eine weitere Möglichkeit besteht darin, die konstanten Parameter und (Längen der Halbachsen) einer Ellipse in ihrer Parameterdarstellung oder in ihrer algebraischen Gleichung durch Funktionen zu ersetzen.
Man kann eine Ellipse als die Menge der Punkte definieren, für die die Summe der Abstände zu den beiden Brennpunkten und konstant ist . Ersetzt man nun diese Summe der Abstände durch eine gewichtete Summe , so bildet die Punktmenge ein Oval, das nur noch eine Symmetrieachse besitzt, auf der ein spitzes und ein stumpfes Ende liegen. Ein solches Oval wird auch als Kartesisches Oval bezeichnet.
Das Konstruktionsverfahren von de La Hire erzeugt eine Ellipse mit Hilfe zweier konzentrischer Kreise. Verschiebt man nun den Mittelpunkt des äußeren Kreises ein wenig und behält sonst aber die restlichen Schritte des Konstruktionsverfahrens bei, dann erhält man ein (neues) Oval. Dieses besitzt eine Symmetrieachse, wenn man den Mittelpunkt des äußeren Kreises entlang der Ellipsenachsen verschiebt. Verschiebt man den Mittelpunkt außerhalb der Achsen, dann entsteht ein Oval ohne Symmetrieachsen.
 Ellipse:
Ellipse: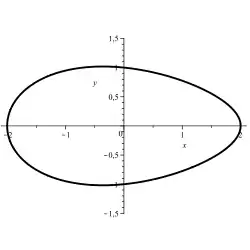
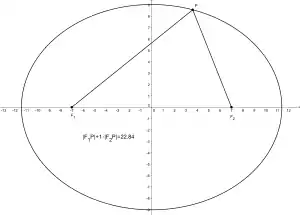 Ellipse:
Ellipse: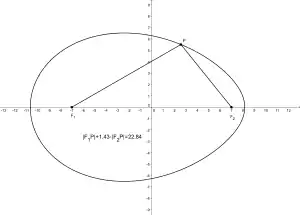
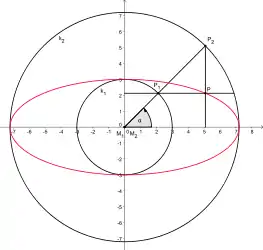 Konstruktion mit konzentrischen Kreisen
Konstruktion mit konzentrischen Kreisen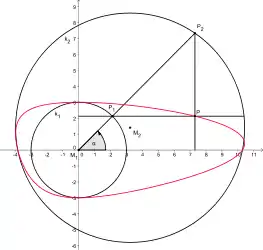 Konstruktion mit exzentrischen Kreisen
Konstruktion mit exzentrischen Kreisen
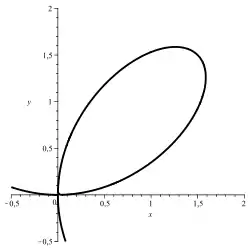
Die Lösungsmenge einer Gleichung mit zwei Unbekannten beziehungsweise bestimmte Teilmengen von ihr lassen sich oft als Kurven in der Ebene auffassen. Bei einer geeigneten Gleichung erhält man dabei ein Oval. Wenn eine solche Lösungskurve kein Oval ist, dafür aber eine konvexe Schlaufe besitzt, so kann durch Hinzufügen eines Korrekturterms aus der Schlaufe ein Oval erzeugt werden.
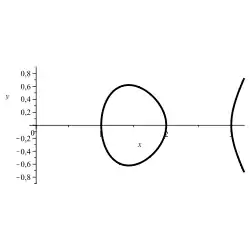
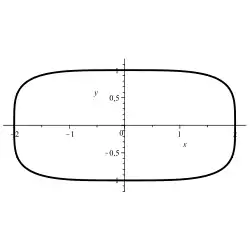
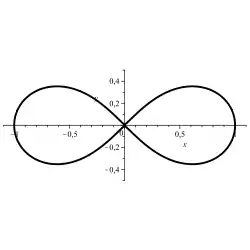
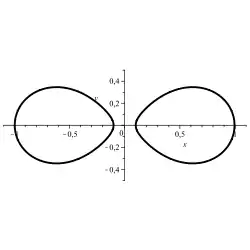
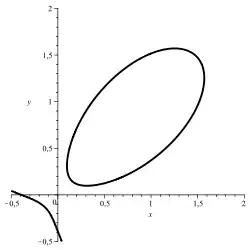
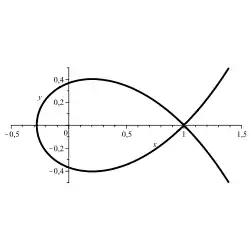 Szegö-Kurve:
Szegö-Kurve: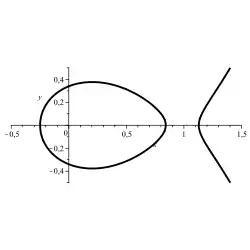
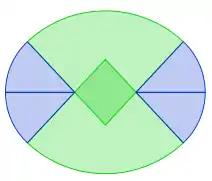
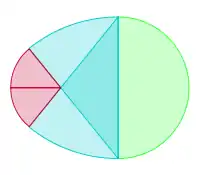
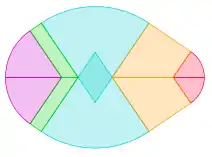
Aus Kreisbögen und Geraden
Ovale lassen sich auch aus Kreisbögen und Geradenstücken zusammensetzen. Allerdings besitzen solche Ovale eine geringere Glattheit als in der obigen Definition gefordert, da sie lediglich in und nicht in liegen. Sie sind damit zwar noch glatt im Sinne einer stetigen Ableitung, besitzen jedoch keine stetige Krümmung mehr. Die Krümmung ist stattdessen auf den Teilabschnitten konstant und besitzt an den Nahtstellen der Kreisbögen bzw. Geradenstücke eine Unstetigkeitsstelle.
 |
 |
 |
 |
| Ovale zusammengesetzt aus Kreisbögen und Geradenstücken | |||
Literatur
- A.B. Ivanov: Oval. In: Michiel Hazewinkel (Hrsg.): Encyclopedia of Mathematics. Springer-Verlag und EMS Press, Berlin 2002, ISBN 978-1-55608-010-4 (englisch, online).
- Helmut Reckziegel, Markus Kriener, Knut Pawel: Elementare Differentialgeometrie mit Maple. Vieweg+Teubner-Verlag 1998, ISBN 978-3-528-06991-9, S. 43ff (Auszug in der Google-Buchsuche)
- Volkmar Wünsch: Differentialgeometrie: Kurven und Flächen. Vieweg+Teubner-Verlag 1997, ISBN 978-3-8154-2095-9, S. 92ff (Auszug in der Google-Buchsuche)
- John A. Adam: A Mathematical Nature Walk. Princeton University Press 2009, ISBN 978-0-691-12895-5, S. 124–136
- Charles Hutton: A Philosophical and Mathematical Dictionary. Band 2, 1815, S. 141 (vollständige Online-Version in der Google-Buchsuche-USA)
- Arnold Emch: Some Properties of Closed Convex Curves in a Plane. American Journal of Mathematics, Band 35, Nr. 4 (Okt., 1913), S. 407–41 (JSTOR 2370404)
- N. Hansen Ball: On Ovals. The American Mathematical Monthly, Band 37, Nr. 7 (Aug. – Sep., 1930), S. 348–353 (JSTOR 2299271)
Weblinks
- Eric W. Weisstein: Oval. In: MathWorld (englisch).
- Norbert Harthun, Iris Rennert: Die Ei-Kurve als Schnitt des Hyperbolischen Kegels (PDF; 158 kB)
- Egg curves auf mathematische-basteleien.de (englisch)
- Paul L. Rosin: On the Construction of Ovals (englisch; PDF; 395 kB)
- André Heck: Mathematical Brooding over an Egg. In Loci, August 2008 – Online-Journal der MAA
- Egg Math – Sammlung von webbasierten Unterrichtseinheiten zur Mathematik rundum das Ei (englisch)
Einzelnachweise
- Heinrich Behnke: Fundamentals of Mathematics. MIT Press 1974, ISBN 978-0-262-02069-5, S. 572 (Auszug in der Google-Buchsuche)
- Oval in der Encyclopaedia of Mathematics (englisch)
- Helmut Reckziegel, Markus Kriener, Knut Pawel: Elementare Differentialgeometrie mit Maple. Vieweg+Teubner Verlag 1998, ISBN 978-3-528-06991-9, S. 43ff (Auszug in der Google-Buchsuche)
- Volkmar Wünsch: Differentialgeometrie: Kurven und Flächen. Vieweg+Teubner Verlag 1997, ISBN 978-3-8154-2095-9, S. 92ff (Auszug in der Google-Buchsuche)
- Catherine Cavagnaro, William T. Haight: Dictionary of Classical and Theoretical Mathematics. CRC Press 2001, ISBN 978-1-58488-050-9, S. 88 (Auszug in der Google-Buchsuche)
- Robert Clarke James, Glenn James: Math Dictionary. Springer 1992, ISBN 978-0-412-99041-0, S. 300 (Auszug in der Google-Buchsuche)
- Ian R. Porteous: Geometric Differentiation. Cambridge University Press 2001, ISBN 978-0-521-00264-6, S. 36 (Auszug in der Google-Buchsuche)