Vierscheitelsatz

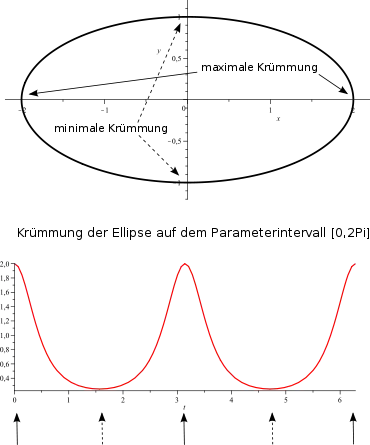
Der Vierscheitelsatz ist ein Satz der Differentialgeometrie über Kurven in der Ebene. Er besagt, dass bei jeder einfach geschlossenen, glatten ebenen Kurve die Krümmungsfunktion mindestens vier Extremstellen besitzt. Punkte einer Kurve, an denen die Krümmung ein lokales Extremum besitzt (also ein lokales Maximum oder Minimum), heißen Scheitel (vgl. Scheitelpunkt).

Vierscheitelsatz bei der Ellipse

Der Satz wurde 1909 für konvexe Kurven vom indischen Mathematiker Syamadas Mukhopadhyaya (1866–1937)[1][2] bewiesen und im allgemeinen Fall von Adolf Kneser 1912[3][2].

Es gibt auch einen Umkehrsatz: jede stetige reelle Funktion auf dem Kreis mit mindestens zwei lokalen Maxima und zwei lokalen Minima ist die Krümmungsfunktion einer ebenen einfachen geschlossenen Kurve. Der Satz wurde für positiv definite Funktionen 1971 von Herman Gluck[4][2] bewiesen und im allgemeinen Fall von Björn Dahlberg (1998).[5][2]

Literatur

Christian Bär: Elementare Differentialgeometrie. Walter de Gruyter, Berlin u. a. 2001, ISBN 3-11-015519-2, S. 57 (Auszug (Google)).
Dennis DeTurck, Herman Gluck, Daniel Pomerleano, David Shea Vick: The Four Vertex Theorem and Its Converse (PDF-Datei; 1,47 MB). In: Notices of the American Mathematical Society. Bd. 54, No. 2, Februar 2007, ISSN 0002-9920, S. 192–207.
W. C. Graustein: Extensions of the Four-Vertex Theorem. Transactions of the American Mathematical Society, Band 41, Nr. 1 (Jan., 1937), S. 9–23 (JSTOR 1989876)

Weblinks

Britta Meixner, Ana-Catalina Plesa: Differentialgeometrie (PDF-Datei; 1,91 MB). Vorlesungsmitschrift Uni Passau, Juli 2006, S. 31–46
Sebastian Klein: Kurven und Flächen. Vorlesungsskript Uni Mannheim, Wintersemester 2008, S. 35

Einzelnachweise

Mukhopadhyaya: New methods in the geometry of a plane arc, Bull. Calcutta Math. Soc. 1, 1909, 21–27
Dennis DeTurck, Herman Gluck, Daniel Pomerleano, David Shea Vick: The Four Vertex Theorem and Its Converse (PDF-Datei; 1,47 MB). In: Notices of the American Mathematical Society. Bd. 54, No. 2, Februar 2007, ISSN 0002-9920, S. 192–207.
Kneser: Bemerkungen über die Anzahl der Extrema der Krümmung auf geschlossenen Kurven und über verwandte Fragen in einer nicht euklidischen Geometrie, Festschrift Heinrich Weber. Teubner. 1912, S. 170–180
Gluck, The converse to the four-vertex theorem, L'Enseignement Math. 17, 1971, 295–309
Dahlberg, The converse of the four vertex theorem, Proc. Amer. Math. Soc. 133, 2005, S. 2131–2135

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Mukhopadhyaya: New methods in the geometry of a plane arc, Bull. Calcutta Math. Soc. 1, 1909, 21–27

[AMS-2] Dennis DeTurck, Herman Gluck, Daniel Pomerleano, David Shea Vick: The Four Vertex Theorem and Its Converse (PDF-Datei; 1,47 MB). In: Notices of the American Mathematical Society. Bd. 54, No. 2, Februar 2007, ISSN 0002-9920, S. 192–207.

[3] Kneser: Bemerkungen über die Anzahl der Extrema der Krümmung auf geschlossenen Kurven und über verwandte Fragen in einer nicht euklidischen Geometrie, Festschrift Heinrich Weber. Teubner. 1912, S. 170–180

[4] Gluck, The converse to the four-vertex theorem, L'Enseignement Math. 17, 1971, 295–309

[5] Dahlberg, The converse of the four vertex theorem, Proc. Amer. Math. Soc. 133, 2005, S. 2131–2135