Orbitalordnung
Als Orbitalordnung bezeichnet man eine räumlich periodische Modulation der Besetzung von Atomorbitalen durch Valenzelektronen in Festkörpern (Abbildung 1).
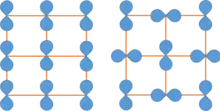
Ein solches Ordnungsmuster ist häufig verbunden mit richtungsabhängigen (anisotropen) magnetischen, optischen und Transport-Eigenschaften. Es kann verursacht werden durch
- Wechselwirkungen zwischen den Valenzelektronen und dem Kristallgitter
- magnetische Korrelationen,
die in den beiden folgenden Kapiteln näher beschrieben werden.
Kooperativer Jahn-Teller-Effekt
In Molekülen mit entarteten Valenzorbitalen kann eine strukturelle Verzerrung die Energie des Grundzustands senken, was als „Jahn-Teller-Effekt“ bezeichnet wird.
Der Effekt wirkt auch in Festkörpern mit entarteten Valenzorbitalen, welche ihre Grundzustandsenergie durch eine Verzerrung der Elementarzelle senken können; hier wird er als „kooperativer“ Jahn-Teller-Effekt bezeichnet, da die Verzerrungen benachbarter Elementarzellen gekoppelt sind. Dies führt dieser zu einer Erniedrigung der Kristallsymmetrie und zu einer regelmäßig alternierenden Orbitalbesetzung.
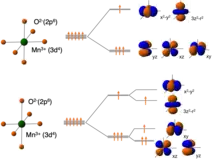
Ein bekanntes Beispiel ist Lanthan-Manganat (LaMnO3) mit Mn3+-Ionen in der Valenzelektronen-Konfiguration 3d4. Die Kristallstruktur von LaMnO3 ist die Perowskit-Struktur, in der diese Ionen von einem kubischen Oktaeder aus sechs negativ geladenen Sauerstoff-Ionen (O2-) umgeben sind (Abbildung 2, oben).
Durch die elektrische Abstoßung zwischen den Valenzelektronen und den O2--Liganden spalten sich die Energieniveaus der d-Orbitale in zwei Gruppen auf:
- Die x2-y2- und 3z2-r2-Orbitale in der eg-Gruppe sind direkt auf die benachbarten O2--Ionen ausgerichtet und haben daher eine höhere Energie.
- Die xy-, xz- und yz-Orbitale in der t2g-Gruppe sind hingegen auf die Zwischenräume ausgerichtet, so dass die Distanz der Elektronen zu den O2--Ionen größer und die Energie entsprechend niedriger ist.
Die Besetzung dieser Orbitale ergibt sich aus den Hund’schen Regeln: In der t2g-Gruppe sind alle drei Orbitale durch jeweils ein Elektron besetzt, so dass keine Entartung vorliegt. Das vierte Elektron besetzt dann eines der zwei entarteten eg-Orbitale.
Beim Abkühlen verzerren sich die MnO6-Oktaeder, so dass vier O2--Ionen näher an das Mn3+-Ion heranrücken, während sich die übrigen zwei weiter davon entfernen (Abbildung 2, unten). Diese tetragonale Verzerrung des Oktaeders hebt die Entartung der eg-Orbitale auf. Die Energie des x2-y2-Orbitals, welches auf die näher benachbarten O2--Ionen ausgerichtet ist, erhöht sich. Entsprechend erniedrigt sich die Energie des Orbitals mit 3z2-r2 Symmetrie, welches auf die weiter entfernten Sauerstoff-Ionen ausgerichtet ist. Letzteres Orbital wird durch das Elektron besetzt, während ersteres unbesetzt bleibt. Da sich so also die Energie des Grundzustands erniedrigt, erfolgt die Verzerrung des Oktaeders spontan bei genügend tiefen Temperaturen. Die Verzerrungen benachbarter Oktaeder in Kristallgitter sind durch die gemeinsamen O2--Ionen gekoppelt, so dass sich die Elementarzelle des Gitters durch die Verzerrung verdoppelt und eine regelmäßige Orbitalordnung entsteht (Abbildung 3). Ein struktureller Phasenübergang in die orbital geordnete Phase findet in LaMnO3 bei 780 K statt.[1] Orbitalordnung wird auch in dotierten Manganaten und anderen Metalloxiden beobachtet, z. B. bei Kobaltaten.
Orbitalordnung und Magnetismus
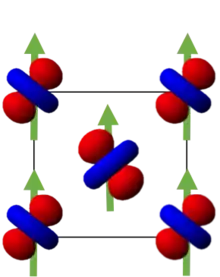
Die relative Ausrichtung der Valenzorbitale auf benachbarten Gitterplätzen bestimmt das Vorzeichen und die Größe der Superaustausch-Wechselwirkungen, welche für den Magnetismus in magnetischen Isolatoren verantwortlich sind (z. B. in Metalloxiden).
Dieses Wechselspiel zwischen Orbitalordnung und Magnetismus wurde in den 1960er Jahren u. a. von John Goodenough, Junjiro Kanamori und Philip W. Anderson systematisch untersucht und in den „Goodenough-Kanamori-Anderson“-Regeln zusammengefasst. Die wichtigsten Regeln besagen:
- Ist die Orbitalbesetzung in den beiden Metallionen identisch, so ist die Superaustausch-Wechselwirkung in einer M-O-M-Bindung (M = Metallion) stark und antiferromagnetisch.
- Sind in benachbarten Metallionen orthogonale Orbitale besetzt, so ist die Superaustausch-Wechselwirkung schwach und ferromagnetisch.
Zum Beispiel findet in LaMnO3 bei 140 K ein magnetischer Phasenübergang statt:[2] Unterhalb dieser kritischen Temperatur sind Kristallebenen mit alternierender Orbitalbesetzung ferromagnetisch geordnet (Abbildung 3); dagegen ist die Orbitalbesetzung in der Richtung senkrecht zu diesen Ebenen gleichförmig, und die Richtung der Magnetmomente alterniert.
Die Goodenough-Kanamori-Anderson-Regeln gelten für Verbindungen, in denen die Elektron-Gitter-Wechselwirkung deutlich stärker ist als die Superaustausch-Wechselwirkung, so dass die Orbitalordnung bei sehr viel höheren Temperaturen stattfindet als die magnetische Ordnung. Das ist insbesondere für Metalloxide mit entarteten eg-Orbitalen der Fall, z. B. bei LaMnO3. In anderen Verbindungen (z. B. bei Metalloxiden mit entarteten t2g-Orbitalen) ist die Energieskala beider Wechselwirkungen vergleichbar, so dass magnetische Korrelationen die Orbitalordnung stark beeinflussen können.[3]
Ein von den Physikern Daniel I. Khomskii und Kliment I. Kugel entworfenes Modell[4] vernachlässigt die Elektron-Gitter-Wechselwirkung vollständig, so dass die Orbitalordnung ausschließlich durch magnetische Korrelationen zustande kommt.
Einzelnachweise
- Y. Murakami, J. P. Hill, D. Gibbs, M. Blume, I. Koyama, M. Tanaka, H. Kawata, T. Arima, Y. Tokura, K. Hirota, Y. Endoh: Resonant X-Ray Scattering from Orbital Ordering in LaMnO3. In: Physical Review Letters. Band 81, Nr. 3, 20. Juli 1998, S. 582–585, doi:10.1103/PhysRevLett.81.582 (aps.org [abgerufen am 29. Dezember 2019]).
- Kazuma Hirota, Nobuhisa Kaneko, Akinori Nishizawa, Yasuo Endoh: Two-Dimensional Planar Ferromagnetic Coupling in LaMnO3. In: Journal of the Physical Society of Japan. Band 65, Nr. 12, 15. Dezember 1996, ISSN 0031-9015, S. 3736–3739, doi:10.1143/JPSJ.65.3736 (jps.jp [abgerufen am 29. Dezember 2019]).
- C. Ulrich, G. Khaliullin, M. Guennou, H. Roth, T. Lorenz, B. Keimer: Spin-Orbital Excitation Continuum and Anomalous Electron-Phonon Interaction in the Mott Insulator LaTiO3. In: Physical Review Letters. Band 115, Nr. 15, 9. Oktober 2015, S. 156403, doi:10.1103/PhysRevLett.115.156403 (aps.org [abgerufen am 29. Dezember 2019]).
- K. I. Kugel, D. I. Khomskii: Crystal structure and magnetic properties of substances with orbital degeneracy. April 1973 (englisch, jetp.ac.ru [PDF; 309 kB; abgerufen am 29. Dezember 2019]).