Olberssches Paradoxon

Das olberssche Paradoxon (alternative Schreibweise Olbers’sches Paradoxon) zeigt den sich ergebenden Widerspruch bei der Vorhersage eines hellen Nachthimmels und seiner tatsächlichen dunklen Erscheinung auf.

Graphische Veranschaulichung zum olbersschen Paradoxon

Begriff

Der Begriff wurde von Hermann Bondi 1952 kreiert.[1] Heinrich Wilhelm Olbers formulierte dieses Problem im Jahre 1823,[2] nachdem es bereits von anderen Wissenschaftlern im Zusammenhang mit konkurrierenden kosmologischen Modellen betrachtet worden war. Es betrifft Weltmodelle, die dem perfekten kosmologischen Prinzip entsprechen, d. h., ein unendlich ausgedehntes und unendlich altes Universum postulieren und in diesem eine über große Distanzen gleichmäßige Sternverteilung annehmen. Unter diesen Voraussetzungen müsste das Licht eines Sterns aus jeder Richtung die Erde erreicht haben und der Himmel mindestens so hell wie die Sternenoberfläche erscheinen. Dies widerspricht der Beobachtung eines dunklen Nachthimmels und war ein historisches Argument gegen solche Modelle.

Siehe auch: Oberbegriff Paradoxon

Historische Entwicklung der Modelle

Thomas Digges homogene Sternverteilung in seiner A Perfit Description of the Caelestiall Orbes.

Infolge der kopernikanischen Wende entwickelten sich verschiedene Kosmologien, die sich darin unterschieden, welche Sternenverteilung sie im Universum annahmen. Kopernikus vertrat 1543 in seinem Werk De revolutionibus orbium coelestium die Auffassung, dass sich die Sterne in der äußersten unbeweglichen Schale des Universums befinden. Sein Modell enthält endlich viele Sterne in endlichem Abstand von der Sonne, es ist also inhomogen und hierarchisch.

Thomas Digges erklärte eine solche Fixsternsphäre für wissenschaftlich unhaltbar und schlug 1576 in A Perfit Description of the Caelestial Orbes eine homogene Sternverteilung in einem unendlichen Universum vor. Die Supernova von 1572 war für ihn ein Stern, der aus einer fernen, unsichtbaren Zone näher gekommen und somit sichtbar geworden war.[3] Für Digges war der „größte Teil der Sterne aufgrund der Entfernung unsichtbar.“[4]

Auch von Giordano Bruno und von Galileo Galilei im Sidereus Nuncius (1610) wurde ein unendliches Universum mit unendlich vielen Sonnen postuliert, in dem die beobachteten Fixsterne ferne Sonnen sind.

Aus diesen Modellvorstellungen folgte das Paradoxon, wie es Johannes Kepler 1610 beschrieb.[5] Er hatte damit ein starkes Argument gegen die Unendlichkeit des Universums (bzw. gegen die unendliche Tiefe des Fixsternhimmels).[6]

Im 18. Jahrhundert beschäftigte man sich ebenfalls mit dem Paradoxon, zum Beispiel wurde es von Edmond Halley 1720[7] und Jean-Philippe de Chéseaux erwähnt, auch Johann Heinrich Lambert kannte es.

Olbers’ Formulierung

„Sind wirklich im ganzen unendlichen Raum Sonnen vorhanden, sie mögen nun in ungefähr gleichen Abständen von einander, oder in Milchstrassen-Systeme vertheilt sein, so wird ihre Menge unendlich, und da müsste der ganze Himmel eben so hell sein wie die Sonne. Denn jede Linie, die ich mir von unserem Auge gezogen denken kann, wird nothwendig auf irgend einen Fixstern treffen, und also müsste uns jeder Punkt am Himmel Fixsternlicht, also Sonnenlicht zusenden.“[8]

Exakte Formulierung

Wenn das dreidimensionale Universum folgende Eigenschaften 1. bis 5. erfüllt, dann ist der Himmel auf der Erde nach unendlicher Zeit unendlich hell:

Es ist in jede Richtung unendlich ausgedehnt.
Alle Sterne haben eine endliche Ausdehnung und Leuchtkraft.
Die Anzahl der Sterne $N(R)$ in einer Kugel mit Radius $R$ um die Erde geht für $R\rightarrow \infty$ gegen unendlich wie $R^{3}$ (homogene Sternenverteilung auf kosmologischer Skala).
Die Anzahl der Sterne $N_{S}(R)$ in jedem Ausschnitt dieser Kugel geht für $R\rightarrow \infty$ gegen unendlich wie $R^{3}$ (Isotropie auf kosmologischer Skala in der homogenen Sternenverteilung).
Die Sterne und das Universum ändern sich in beliebigen Zeiten nicht (statisches Universum).

Die in den Bedingungen 1 und 2 genannten Aussagen waren schon im 16. Jahrhundert allgemein anerkannt, die endliche Lebensdauer von Sternen war noch nicht bekannt. Die von Digges postulierte Sternenverteilung, die auf großen Skalen als homogen und isotrop wie in den Bedingungen 3 und 4 zu bezeichnen ist, war eine direkte Reaktion auf die räumlich inhomogene Sternenverteilung von Kopernikus. Wenn eine ewige Lebenszeit der Sterne angenommen wird, hätte auch jetzt bereits unendlich viel Licht die Erde erreicht.

Veranschaulichung des olbersschen Paradoxons

Wald als Analogie zum olbersschen Paradoxon: In jeder (horizontalen!) Blickrichtung steht ein Baum.

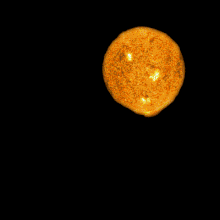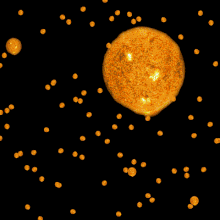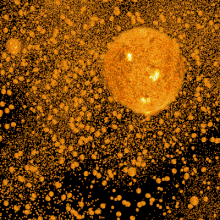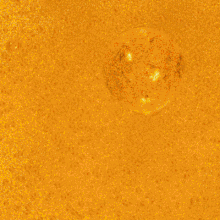
Um das Paradoxon besser zu veranschaulichen, kann man sich die Erde in der Mitte einer Ebene vorstellen. Wäre das Universum überall etwa gleich aufgebaut und unbegrenzt groß, so sähe der Beobachter innerhalb des Abstands r (vergleichbar mit einer Horizontlinie) alle Sterne innerhalb dieses Radius. Dabei nimmt die scheinbare Größe des Himmelskörpers proportional zur Entfernung vom Betrachter ab. Erhöht man diese Sichtlinie um x (r + x), so nimmt die Zahl der Sterne darin quadratisch, also um x² zu, wobei allerdings die sich darin befindlichen Sterne um die Wurzel von x kleiner wirken. Vergleicht man die „Gesamthelligkeit“ der beiden Radien, stellt man fest, dass beide einander entsprechen. Dies bedeutet, dass unabhängig davon, wie weit ein Beobachter auch blicken mag, die kollektive Anzahl an sichtbaren Sternen am Horizont direkt proportional zum Abstand zunehmen würde. Geht man nun auch davon aus, dass das Universum unbegrenzt groß ist und das Licht unbegrenzt Zeit hätte, uns zu erreichen, so würde dies bedeuten, dass es auf der Erde niemals dunkel werden könnte. Damit müsste auch auf der Erde wie an jedem anderen Punkt des Universums die gleiche Temperatur wie auf der Sonne von ca. 6000 K herrschen.

Historische Erklärungen

In der Geschichte des Paradoxons sind viele Vorschläge diskutiert worden, wie es aufzulösen sei. Die nächstliegende Lösung ist die Annahme, dass das Licht ferner Sterne in seiner Ausbreitung behindert wird und dass Staub- und Gaswolken das Sternenlicht absorbieren. Das war die von Olbers vorgeschlagene Lösung. Wie schon John Herschel erkannte, liefert das keine Erklärung, da sich die Wolken so lange aufheizen würden, bis ihre Emission gleich ihrer Absorption ist.

Benoît Mandelbrot diskutiert das olberssche Paradoxon in seinem Buch Fractal Geometry of Nature von 1977. Bei einer hierarchischen (fraktalen) Anordnung von Massen im Universum lässt sich das Paradoxon vermeiden, wie zuerst der Schriftsteller Edmund Edward Fournier d’Albe (1868–1933) in seinem Buch Two New Worlds von 1907 zeigte[9], wobei es Fournier nur auf die Demonstration des Prinzips ankam und nicht um ein realistisches Modell. Von Carl Charlier wurde das 1908 in realistischeren Modellen aufgegriffen, bei denen die fraktale Dimension mit der Größenskala variierte[10], und der überdies solche Cluster-Strukturen in seinen Karten der Galaxienverteilung erkennen wollte. Fournier gab auch ein physikalisches Argument (eine obere Grenze für die beobachtete Sterngeschwindigkeit) für eine fraktale Dimension der Massenverteilung nahe 1 an. Auch Mandelbrot selbst sieht in diesen Versuchen weniger ein Modell für eine Lösung des Paradoxons, das er durch die kosmologischen Standardmodelle als gelöst betrachtet, sondern erste Sichtweisen einer möglichen fraktalen Anordnung der Galaxien im Universum. Untersuchungen der Galaxienverteilung auf verschiedenen Skalen widerlegen aber ein einfaches hierarchisches Modell mit gemeinsamer fraktaler Dimension.[11]

Auflösung des Paradoxons

Die Bedingung eines unendlich großen beobachtbaren Kosmos mit unendlich vielen Sternen, die in der Formulierung des Paradoxons angenommen wurde, ist widerlegt. Beobachtungsdaten von Projekten bzw. Sonden wie COBE und WMAP zeigen, dass das sichtbare Universum in räumlicher und zeitlicher Hinsicht endlich ist. Zwar spricht nichts gegen die Annahme eines unendlich ausgedehnten Universums, da das Universum jedoch ein endliches Alter besitzt und sich Licht nur mit einer endlichen Geschwindigkeit ausbreitet, kann uns seit dem Urknall nur Licht aus einem endlich großen Bereich erreichen. Außerdem besitzen Sterne nur eine endliche Lebensdauer, was die Anzahl der Sterne, deren Licht uns erreichen kann, weiter einschränkt.

Die heute verbreitete Vorstellung zur Erklärung des dunklen Nachthimmels basiert auf der allgemeinen Relativitätstheorie und dem daraus entwickelten aktuellen Lambda-CDM-Modell der Kosmologie.

Heutige Erklärung des dunklen Nachthimmels

Für die Erklärung der genauen Erscheinung unseres Nachthimmels sind noch weitere Effekte zu beachten. Das Paradoxon beschränkte sich auf das Licht von Sternen, wohingegen die meisten Strahlungsquanten im intergalaktischen Medium noch aus der Ära der Entkoppelung der Hintergrundstrahlung stammen. Dieses Licht wurde mit dem Spektrum eines näherungsweise schwarzen Körpers der Temperatur 3000 K ausgesandt und würde bei ungehinderter Ausbreitung den Himmel gleichmäßig gelb/orange erleuchten. Dass dies nicht der Fall ist, liegt an der Expansion des Universums. Der sich ausdehnende Raum verringert die Energie des sich durch ihn bewegenden Lichts, welches dadurch langwelliger wird. Diesen Effekt bezeichnet man als kosmologische Rotverschiebung. Infolge dieser Rotverschiebung ist die Hintergrundstrahlung vom Urknall so energiearm geworden, dass sie heute dem Wärmestrahlungsspektrum eines sehr kalten (2,7 K) schwarzen Körpers entspricht. Dieser sehr langwellige Bereich gehört zur Mikrowellenstrahlung. Er ist für das menschliche Auge unsichtbar und trägt somit nicht zur Himmelshelligkeit bei. Auch das Licht weit entfernter Galaxien wird durch die Expansion des Universums ins für Menschen unsichtbare Infrarot verschoben, wodurch der Infrarothintergrund entsteht.

Selbst bei Annahme der mittlerweile aus anderen Gründen bei der Mehrzahl der Astrophysiker als widerlegt geltenden Steady-State-Theorie genügt die unstreitige Rotverschiebung durch die Expansion unabhängig von der Annahme eines Urknalls prinzipiell zur Lösung des olbersschen Paradoxons.

Literatur

chronologisch

Gerhard Vollmer: Warum wird es nachts dunkel? Das Olberssche Paradoxon als wissenschaftstheoretische Fallstudie. In: Heinz-Dieter Ebbinghaus und Gerhard Vollmer (Hrsg.): Denken Unterwegs. Wissenschaftliche Verlagsgesellschaft, Stuttgart 1992, S. 183–199.
Paul Wesson: Olbers’ paradox and the spectral intensity of the extragalactic background light. In: The Astrophysical Journal. Band 367, 1991, S. 399–406 (englisch).
Edward Harrison: The dark night sky riddle. in: The Galactic and Extragalactic Background Radiation. Proceedings of the 139th. Symposium of the International Astronomical Union, held in Heidelberg. Dordrecht, Boston, 1990, S. 3–17.
Edward Harrison: Darkness at Night: A Riddle of the Universe. Harvard University Press 1987.
Stanley L. Jaki: The Paradox of Olbers’ Paradox. A Case History of Scientific Thought. Herder & Herder, 1969. (Real View Books, Pinckney, Missouri 2000. ISBN 1-892548-10-0).
Wilhelm Olbers: Ueber die Durchsichtigkeit des Weltraums. In: Astronomisches Jahrbuch für 1826. S. 110–121. (Nachdruck in: Wilhelm Olbers, sein Leben und seine Werke. Im Auftrage der Nachkommen herausgegeben von C. Schilling. Berlin 1894.) online.

Weblinks

Commons: Olbers' paradox – Sammlung von Bildern, Videos und Audiodateien

α-Centauri-Videos:

Wieso ist das Universum so dunkel? aus der Fernseh-Sendereihe alpha-Centauri (ca. 15 Minuten). Erstmals ausgestrahlt am 22. Dez. 2004.
Wird sich das Universum wieder zusammenziehen? aus der Fernseh-Sendereihe alpha-Centauri (ca. 15 Minuten). Erstmals ausgestrahlt am 30. Jan. 2000.

deutsch:

Endliche Unendlichkeit des Weltraums – Warum es nachts nicht hell wird – Anmerkungen zum "Olbers’schen Paradoxon" Telepolis
Warum wird es nachts dunkel? (Memento vom 8. August 2007 im Internet Archive) Wissenschaftstheoretische Lehren aus dem olbersschen Paradoxon. (Tobias Riek)
Goehring, Olbers’sches Paradoxon, PDF-Datei (Memento vom 22. Mai 2012 im Internet Archive)

englisch:

P. Lutus: Why is the Sky Dark at Night?
On Olber’s Paradox@mathpages.com
Olbers’ Paradox - by Eduardo Manuel Alvarez@astronomyonline.org
Relativity FAQ about Olbers’ paradox
Astronomy FAQ about Olbers’ paradox
Cosmology FAQ about Olbers’ paradox
Scott, Douglas, and Martin White, The Cosmic Microwave Background

Fußnoten und Einzelnachweise

Edward Harrison: Olbers’ Paradox in recent times. (S. 33–46) in: Bruno Bertotti u. a. (Hrsg.): Modern Cosmology in Retrospect. Cambridge 1990, S. 38 (engl.); Gerhard Günther: Anmerkungen zur Philosophie des Himmels. in: Rolf Fechner, Carsten Schlüter-Knauer (Hrsg.): Existenz und Kooperation. S. 133
Schilling: Wilhelm Olbers, sein Leben und seine Werke, 1894, S. 133 (online)
„It was his belief that the distances to the stars varied that at first seemed to be consistent with the new star being a faint one close to the Earth.“ J. J. O’Connor, E. F. Robertson: Thomas Digges.@University of St Andrews, Scotland (abgerufen 23. März 2014); s. a. Michael Weichenhan: «Ergo perit coelum …» Die Supernova des Jahres 1572 und die Überwindung der aristotelischen Kosmologie. Stuttgart 2004, S. 588
"the greatest part rest by reason of their wonderful distance invisible to us", zitiert nach Michael Weichenhan: «Ergo perit coelum …» Stuttgart 2004, S. 587/588 (online nur S. 587, abgerufen 23. März 2014); s. a. Harry Nussbaumer: Revolution am Himmel: wie die kopernikanische Wende die Astronomie veränderte. Zürich 2011, S. 91
Kepler Dissertatio cum nuncio sidereo galilei, 1610, deutsch Diederichs 1918 (Otto Bryk), englisch von Edward Rosen: Keplers conversation with Galileos Sidereal Messenger, New York, Johnson Reprint, 1965, S. 34.
Paolo Rossi: Die Geburt der modernen Wissenschaft in Europa. übersetzt München 1997, S. 175
Halley wird zitiert in Benoît Mandelbrot The fractal geometry of nature, Freeman 1983, S. 92 Das Kapitel 9 ist der Diskussion des Paradoxons gewidmet, dort Blazing Sky Effect genannt.
Schilling: Wilhelm Olbers, sein Leben und seine Werke, 1894, S. 135 (online)
zu Fournier d’Albe: Mandelbrot, Fractal Geometry of Nature, loc.cit., S. 396
Charlier Wie eine unendliche Welt aufgebaut sein kann, Arkiv för matematik, Astronomi och Fysik, Bd. 4, 1908, S. 1–15 (englisch in Bd. 16, 1922, S. 1–34)
Peebles Principles of Physical Cosmology, Princeton University Press 1993, S. 209–224

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Edward Harrison: Olbers’ Paradox in recent times. (S. 33–46) in: Bruno Bertotti u. a. (Hrsg.): Modern Cosmology in Retrospect. Cambridge 1990, S. 38 (engl.); Gerhard Günther: Anmerkungen zur Philosophie des Himmels. in: Rolf Fechner, Carsten Schlüter-Knauer (Hrsg.): Existenz und Kooperation. S. 133

[2] Schilling: Wilhelm Olbers, sein Leben und seine Werke, 1894, S. 133 (online)

[3] „It was his belief that the distances to the stars varied that at first seemed to be consistent with the new star being a faint one close to the Earth.“ J. J. O’Connor, E. F. Robertson: Thomas Digges.@University of St Andrews, Scotland (abgerufen 23. März 2014); s. a. Michael Weichenhan: «Ergo perit coelum …» Die Supernova des Jahres 1572 und die Überwindung der aristotelischen Kosmologie. Stuttgart 2004, S. 588

[4] "the greatest part rest by reason of their wonderful distance invisible to us", zitiert nach Michael Weichenhan: «Ergo perit coelum …» Stuttgart 2004, S. 587/588 (online nur S. 587, abgerufen 23. März 2014); s. a. Harry Nussbaumer: Revolution am Himmel: wie die kopernikanische Wende die Astronomie veränderte. Zürich 2011, S. 91

[5] Kepler Dissertatio cum nuncio sidereo galilei, 1610, deutsch Diederichs 1918 (Otto Bryk), englisch von Edward Rosen: Keplers conversation with Galileos Sidereal Messenger, New York, Johnson Reprint, 1965, S. 34.

[6] Paolo Rossi: Die Geburt der modernen Wissenschaft in Europa. übersetzt München 1997, S. 175

[7] Halley wird zitiert in Benoît Mandelbrot The fractal geometry of nature, Freeman 1983, S. 92 Das Kapitel 9 ist der Diskussion des Paradoxons gewidmet, dort Blazing Sky Effect genannt.

[8] Schilling: Wilhelm Olbers, sein Leben und seine Werke, 1894, S. 135 (online)

[9] zu Fournier d’Albe: Mandelbrot, Fractal Geometry of Nature, loc.cit., S. 396

[10] Charlier Wie eine unendliche Welt aufgebaut sein kann, Arkiv för matematik, Astronomi och Fysik, Bd. 4, 1908, S. 1–15 (englisch in Bd. 16, 1922, S. 1–34)

[11] Peebles Principles of Physical Cosmology, Princeton University Press 1993, S. 209–224