Johann Heinrich Lambert
Johann Heinrich Lambert (* 26. August 1728 in Mülhausen (Elsass); † 25. September 1777 in Berlin) war ein schweizerisch-elsässischer Mathematiker, Logiker, Physiker und Philosoph der Aufklärung, der u. a. die Irrationalität der Zahl Pi bewies.

(Lithographie von Godefroy Engelmann, 1829)
Leben
Lambert entstammte einer verarmten hugenottischen Flüchtlingsfamilie, die sich im damals zur schweizerischen Eidgenossenschaft gehörigen Mülhausen im Elsass niedergelassen hatte. Sein Vater war Schneider. Trotz auffallend guter Leistungen musste der Sohn bereits als Zwölfjähriger die Stadtschule verlassen und als Gehilfe des Vaters tätig werden. Er bildete sich aber selbst weiter mit Hilfe aller für ihn erreichbaren Bücher. Später arbeitete er als Buchhalter, danach ab 1746 als Privatsekretär bei Isaak Iselin in Basel und zwei Jahre später als Hauslehrer beim Reichsgrafen Peter von Salis in Chur. Mit dessen Kindern unternahm er zwischen 1756 und 1758 mehrere Bildungsreisen, und er wurde Mitglied der schweizerischen Société scientifique in Basel. 1755 erfolgten seine ersten Veröffentlichungen (über Wärmelehre). Im Rahmen der Grand Tour mit seinen Schülern besuchte er Göttingen (Abraham Kästner, Tobias Mayer), wo er Mitglied der Göttinger Gesellschaft der Wissenschaften[1] wurde, wich vor dem Siebenjährigen Krieg nach Utrecht und den Niederlanden aus, wo er mit seinen Schülern zwei Jahre blieb und er sein erstes Buch (über Optik) 1758 in Den Haag drucken ließ, und Paris, wo er Jean-Baptiste le Rond d’Alembert traf.
1758 war Lambert wohnhaft in Augsburg und trat dem Kreis der Gründungsmitglieder der „Churfürstlichen Akademie der Wissenschaften“, der späteren Bayerischen Akademie der Wissenschaften hinzu, in deren Philosophischer Klasse er 1759 auswärtiges Mitglied wurde. Er unternahm optische Experimente und ließ in Augsburg zwei Bücher drucken (über Photometrie und Kosmologie). Pläne auf eine Professur in Göttingen zerschlugen sich. 1764 wurde er auf Vorschlag von Leonhard Euler (der ihn schon 1760 für eine Astronomie-Professur in Sankt Petersburg vorgeschlagen hatte) zum Mitglied der Akademie der Wissenschaften in Berlin ernannt und erhielt 1770 eine gut dotierte Stelle als Oberbaurat und „Membrum honorarium“ beim neugeschaffenen Oberbaudepartement.[2] Anfangs gab es Schwierigkeiten mit Friedrich dem Großen wegen des exzentrischen Auftretens von Lambert, die sich aber legten, als Friedrich dessen wissenschaftliche Bedeutung erkannte. In Berlin kam es zur Eintrübung des Verhältnisses zu Euler über Fragen der Finanzierung der Akademie – Euler ging 1766 nach Sankt Petersburg. Lambert veröffentlichte bis zu seinem frühen Tod mit nur 49 Jahren 150 Abhandlungen in den Mitteilungen der Preußischen Akademie.
Leistungen
Lambert gehörte zu den hervorragendsten Mathematikern und Logikern seiner Zeit. Die Lehre von der Intensitätsmessung des Lichts begründete er als Wissenschaft in seinem Werk Photometria sive de mensura et gradibus luminis, colorum et umbrae (Augsburg 1760). Weiter erforschte er – selbst seit seiner Geburt schwerhörig – die Theorie des Sprachrohrs.
Vor allem in der Photometria, aber auch in seinem Buch Beyträge zum Gebrauche der Mathematik und deren Anwendung (Vol. 1, 1765), verknüpfte er Ideen von Thomas Simpson, Rugjer Josip Bošković und Mayer. Seine Arbeit in der Photometrie und Geodäsie führte ihn zu einer allgemeinen Theorie der Fehler. Er diskutierte das Problem der Anwendung von Wahrscheinlichkeitsverteilungen auf Fehlerterme und verwendete bereits eine Maximum-Likelihood-Methode für die Bestimmung von Mittelwerten.
Außerdem erwarb sich der aufgeklärte Gelehrte Verdienste um die Erkenntnistheorie, der er sein Werk Neues Organon, oder Gedanken über die Erforschung und Bezeichnung des Wahren (2 Bde., Leipzig 1764) widmete. Das Werk gliederte er in vier Teile: Im ersten Band finden sich Dianoiologie (oder die Lehre von den Gesetzen des Denkens) und Alethiologie (oder die Lehre von der Wahrheit). Im zweiten Band werden die Semantik bzw. Semiotik (Zeichenlehre) und abschließend die Phänomenologie behandelt (worunter Lambert die Lehre des Scheins versteht).
Nach seinen eigenen Worten aus der Einleitung ist das Werk insbesondere von Christian Wolff und John Locke inspiriert, wobei er sich im ersten Teil, der Dianoiologie, besonders an Wolff orientiert habe. Tatsächlich bestehen viele Ähnlichkeiten zu Wolffs Werk Vernünftige Gedanken von den Kräften des menschlichen Verstandes. Jedoch stellt Lambert auch klar, er habe nicht nur Wolffs Ideen übernommen, sondern sie auch um eigene Einsichten erweitert. Anliegen seiner Arbeit war es, mit Hilfe der Mathematik eine bessere Methodik für die Philosophie zu schaffen. Er gilt als ein Wegbereiter des modernen Rationalismus und bedeutender Vorgänger von Immanuel Kant, mit dem er von 1765 bis 1770 korrespondierte.
1759 erschien die erste Auflage seiner Schrift Freye Perspective, die ihn weithin bekannt machte, 1774 die zweite Auflage. Die Schriften zur Perspektive sind 1943 von Max Steck herausgegeben und mit einer ausführlichen Bibliografie aller Werke Lamberts versehen worden.
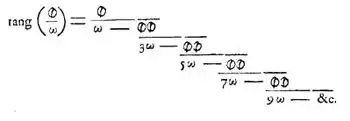
1761 (im Druck 1768) wies Lambert die Irrationalität der Kreiszahl mit Hilfe der Theorie der Kettenbrüche nach.[3] Er bewies darüber hinaus, dass und für rationale Argumente ungleich Null irrational sind. Lambert vermutete ferner, dass e und transzendente Zahlen sind.
Er unternahm die erste systematische Studie der Hyperbelfunktionen, lieferte wichtige Beiträge zur sphärischen Trigonometrie und war ein Pionier der Nichteuklidischen Geometrie: in seiner Theorie der Parallellinien von 1766 bewies er viele Sätze der nichteuklidischen Geometrie, indem er von der Nicht-Gültigkeit des Parallelenaxioms ausging.
1772 entwickelte er mehrere Kartenprojektionen, darunter die häufig verwendete winkeltreue Kegelprojektion. Im selben Jahr veröffentlichte er auch die Lambertsche Farbenpyramide.
1774 begründete er mit Johann Elert Bode das Tafelwerk Berliner Astronomisches Jahrbuch. Seine Methode der Bahnbestimmung von Kometen fand die Bewunderung von Joseph-Louis Lagrange. Sein Buch über Kosmologie (Kosmologische Briefe 1761) stellte das Universum als Ansammlung von Galaxien von Sternen dar.
Nach ihm wurde die angloamerikanische Maßeinheit der Leuchtdichte Lambert benannt. Weiter nach ihm benannt wurden der 1878 entdeckte Asteroid (187) Lamberta sowie jeweils ein Krater (Lambert)[4][5] auf dem Erdmond und dem Planeten Mars.
Der Mathematiker Georg Faber (1877–1966) schrieb 1959 über Lambert:
„Lambert war in Licht und Schatten das rechte Bild eines Gelehrten des 18. Jahrhunderts, der über Gott und die Welt alles mögliche schreibt, aber nicht von einem Katheder aus doziert. Unter den rund 2500 Mitgliedern, welche die (Münchner) Akademie in den zweihundert Jahren ihres Bestehens hatte, findet sich kein zweiter seinesgleichen.“
Schriften
- Les propriétés remarquables de la route de la lumière par les airs et en général par plusieurs milieux réfringens, sphériques et concentriques. (La Haye 1758)
- Die freie Perspektive oder Anweisung jeden perspektivischen Aufriß von freyen Stücken und ohne Grundriß zu verfertigen. (Zürich 1759)
- Photometria sive de mensura et gradibus luminis, colorum et umbrae. (Basel 1760)
- Insigniores orbitae cometarum proprietates. (Basel 1761)
- Cosmologische Briefe über die Einrichtung des Weltbaues. (Augsburg 1761) Digitalisat und Volltext im Deutschen Textarchiv, Digitalisat
- Neues Organon oder Gedanken über die Erforschung und Bezeichnung des Wahren und dessen Unterscheidung vom Irrthum und Schein. (Leipzig 1764) Digitalisat und Volltext im Deutschen Textarchiv Bd. 1, Digitalisat und Volltext im Deutschen Textarchiv Bd. 2
- Beyträge zum Gebrauche der Mathematik und deren Anwendung. 3 Bände (Berlin 1765, 1770, 1772)
- Anmerkungen über die Gewalt des Schiesspulvers und den Widerstand der Luft. (Dresden 1766) Digitalisat
- Zusätze zu den logarithmischen und trigonometrischen Tabellen, zur Erleichterung und Abkürzung der bey Anwendung der Mathematik vorfallenden Berechnungen. (Berlin 1770)
- Anlage zur Architektonik oder Theorie des Einfachen und Ersten in der philosophischen und mathematischen Erkenntniß. 2 Bände. (Hartknoch, Riga 1771) Digitalisat und Volltext im Deutschen Textarchiv Bd. 1, Digitalisat und Volltext im Deutschen Textarchiv Bd. 2
- Beschreibung einer mit dem Calauschen Wachse ausgemalten Farbenpyramide, wo die Mischung jeder Farben aus Weiß und drey Grundfarben angeordnet, dargelegt und derselben Berechnung und vielfacher Gebrauch gewiesen wird. (Berlin 1772) Digitalisat
- Pyrometrie oder vom Maaße des Feuers und der Wärme. (Berlin 1779)
- Deutscher gelehrter Briefwechsel. Hrsg. von Johann III Bernoulli. 5 Bände (Berlin 1782–1785)
- Logische und Philosophische Abhandlungen. Hrsg. von Joh. III Bernoulli. 2 Bände. (Dessau 1782 und 1784)
- Philosophische Schriften. 10 Bde. in 13 Bdn. Begonnen von Hans Werner Arndt, Fortgeführt von Lothar Kreimendahl. Hildesheim: Georg Olms, 1965–2008
- Johann Heinrich Lamberts Monatsbuch. Neu hrsg., eingel., komm. u. mit Verzeichnissen zu Lamberts Schriften, Briefen u. nachgelassenen Manuskripten vers. von Niels W. Bokhove u. Armin Emmel. 2 Bde. (= Philosophische Schriften, Supplement). Hildesheim: Georg Olms, 2020.
Primärtexte
- Texte zur Systematologie und zur Theorie der wissenschaftlichen Erkenntnis. Hrsg. v. Geo Siegwart. Meiner, Hamburg 1988, ISBN 978-3-7873-0723-4
Literatur
- Friedrich L. Bauer: Johann Heinrich Lambert (1728–1777). In: Akademie aktuell – Zeitschrift der Bayerischen Akademie der Wissenschaften. 1/2006, S. 12–15 (PDF; 260 kB)
- Andreas Kraus: Lambert, Johann Heinrich. In: Neue Deutsche Biographie (NDB). Band 13, Duncker & Humblot, Berlin 1982, ISBN 3-428-00194-X, S. 437–439 (Digitalisat).
- Ernst Laas: Lambert, Johann Heinrich. In: Allgemeine Deutsche Biographie (ADB). Band 17, Duncker & Humblot, Leipzig 1883, S. 552–556.
- A. Fuchs: Lambert logicien: notes de lecture du 'Neues Organon' (Leipzig 1764). Strasbourg, 1977.
- Daniel Huber (Hrsg.): Johann Heinrich Lambert: nach seinem Leben und Wirken, aus Anlaß der zu seinem Andenken begangenen Secularfeier in drei Abhandlungen dargestellt. Basel 1829. – Enthält: Matthias Graf, "Johann Heinrich Lambert's Leben"; Simon Erhardt, "Lambert's Verdienste um die theoretische Philosophie"; Daniel Huber, "Versuch über die Verdienste Lambert's in den mathematischen und physischen Wisschenschaften".
- J. Lepsius: J.H. Lambert. Eine Darstellung seiner kosmologischen und philosophischen Leistungen. München, 1881.
- J. Lepsius: Das neue Organon und die Architektonik Lamberts. München, 1881.
- O. Baensch: J.H. Lamberts Philosophie und seine Stellung zu Kant. Tübingen/Leipzig, 1902; Hildesheim, 1972.
- Roger Jaquel: Le savant et philosophe mulhousien Jean-Henri Lambert (1728-1777). Études critiques et documentaires. Paris, 1977.
- "La théorie des parallèles de Johann Heinrich Lambert : Présentation, traduction et commentaires", A. Papadopoulos and G. Théret, Collection Sciences dans l'histoire, Librairie Albert Blanchard, Paris, 2014. ISBN 978-2-85367-266-5.
- Max E. Eisenring: Johann Heinrich Lambert und die wissenschaftliche Philosophie der Gegenwart. November 1941 (online [PDF] Dissertation, ETH Zürich).
- Colloque international et interdisciplinaire Jean-Henri Lambert. Mulhouse, 26-30 septembre 1977, Univ. de Haute-Alsace. Publ. avec le concours du Centre National de la Recherche Scientifique. Paris 1979.
- Felix Humm: J.H. Lambert in Chur 1748-1763 (Reihe Historia raetica, 2). Chur 1972.
- Fabio Todesco: Riforma della metafisica e sapere scientifico. Saggio su J.H. Lambert (1728-1777). Milano 1987.
- Robert Zimmermann: "Lambert, der Vorgänger Kant's. Ein Beitrag zur Vorgeschichte der Kritik der reinen Vernunft", in: Denkschriften der Kaiserlichen Akademie der Wissenschaften, Wien, philosophisch-historische Classe, XXIX. Bd. Wien 1879.
- Friedrich Löwenhaupt (Hrsg.): Johann Heinrich Lambert: Leistung und Leben. Mulhouse 1943.
- Gerhard Jackisch: Johann Heinrich Lamberts “Cosmologische Briefe.” Berlin 1979.
Weblinks
- Nachlass Johann Heinrich Lambert in der Universitätsbibliothek Basel
- Johann Heinrich Lambert (1728-1777): Collected Works – Sämtliche Werke Online (mit Biografie und Briefwechsel (engl.))
- Arbeitsstelle Lambert-Edition, Universität Mannheim
- Literatur von und über Johann Heinrich Lambert im Katalog der Deutschen Nationalbibliothek
- Werke von und über Johann Heinrich Lambert in der Deutschen Digitalen Bibliothek
- Publikationen von und über Johann Heinrich Lambert im Katalog Helveticat der Schweizerischen Nationalbibliothek
- John J. O’Connor, Edmund F. Robertson: Johann Heinrich Lambert. In: MacTutor History of Mathematics archive.
- Spektrum.de: Johann Heinrich Lambert (1728–1777) 1. September 2017
- Einige Bücher Lamberts bei Google Books
- Werkübersicht von Lambert Digitalisate (Memento vom 21. Juli 2011 im Internet Archive) – Service Commun de Documentation (SCD) der Universitäten von Strasbourg
Einzelnachweise
- uni-mannheim.de: Daten zur Biografie Johann Heinrich Lamberts (Memento des Originals vom 31. August 2017 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.
- GStA PK I. HA GD, Abt. 30, I, Nr. 22
- Miklós Laczkovich: On Lambert’s Proof of the Irrationality of π. In: The American Mathematical Monthly. Band 104, Nr. 5, Mai 1997, S. 439–443, doi:10.2307/2974737.
- Johann Heinrich Lambert im Gazetteer of Planetary Nomenclature der IAU (WGPSN) / USGS
- Johann Heinrich Lambert im Gazetteer of Planetary Nomenclature der IAU (WGPSN) / USGS