Oberflächenrekonstruktion
Bei einer Grenzfläche oder Oberfläche eines Kristalls liegt Oberflächenrekonstruktion vor, wenn die Atome nahe bei der Oberfläche gegenüber ihren Positionen im räumlichen Kristallgitter verschoben sind. In einem idealen Kristall sind die Atome in einem regelmäßigen Gitter angeordnet; hüpft man gedanklich von einem zu einem anderen gleichartigen Atom, sieht das Kristallgitter völlig identisch aus. An der Oberfläche des realen Kristalls fehlen auf der Außenseite alle Atome an den Gitterplätzen. Da die Atome im Inneren des Kristalls regelmäßig angeordnet sind, trifft das auch für jede ebene Oberfläche zu, die Grundstruktur ist durch die des Volumenkristalls gegeben. Sind die Atome in der Nähe der Oberfläche, also in den obersten 1 bis 2 Lagen, gegenüber ihren Gitterplätzen im Inneren des Kristalls verschoben, spricht man von Oberflächenrekonstruktion. Sind die Atome nur senkrecht zur Oberfläche verschoben, spricht man von Oberflächenrelaxation.
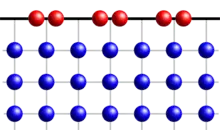
Eigenschaften der Oberflächenrekonstruktion
Analog zur Struktur von dreidimensionalen Kristallen bilden Oberflächen zweidimensionale Kristallstrukturen aus. Aus der Volumen-Kristallstruktur und der Kristallebene der Oberfläche ergibt sich gedanklich die Struktur der nicht rekonstruierten Oberfläche. In dieser Oberfläche entspricht die Anordnung der Atome derjenigen in der entsprechenden Kristallfläche des Volumenkristalls, sie hat beispielsweise in einer (001)-Ebene eines Kristalls im kubischen Kristallsystem also eine quadratische Struktur. Ebenso wie im Volumenkristall bekommt man mit Bravais-Gittern eine Systematik für die verschiedenen möglichen Strukturen. Es gibt insgesamt fünf zweidimensionale Bravais-Gitter.
Eine Rekonstruktion hat dann eine Überstruktur, wenn die Größe der Elementarzelle (EZ) in einer oder beiden Richtungen vervielfacht ist. Wechseln sich in die eine Oberflächenrichtung zwei verschieden rekonstruierte EZ der unrekonstruierten Oberfläche ab und gleichen sich die EZ in der zweiten Richtung, verdoppelt sich die Größe der rekonstruierten EZ in die eine Richtung, während sie in der zweiten Richtung unverändert bleibt, es handelt sich also um eine (2×1)-Überstruktur der Oberfläche. Auch nicht-ganzzahlige Überstrukturen können sich ergeben, zum Beispiel eine (√2,√2)-Überstruktur, in der die Diagonalen der unrekonstruierten die rekonstruierte Elementarzelle bilden[1].
Grund für die Ausbildung von Oberflächenrekonstruktionen ist die Verringerung der freien Energie. In vielen Fällen hat eine rekonstruierte Oberfläche auch die geringste Gesamtenergie (Oberflächenenergie) und ist auch am absoluten Nullpunkt die günstigste Oberflächenstruktur. Auf vielen Materialien können unter gleichen Bedingungen verschiedene Oberflächenstrukturen hervorgerufen werden, die energetisch verschieden günstig sein können. Man erreicht die verschiedenen Strukturen durch verschiedene Präparationsverfahren.[2]
Adsorbatatome oder -moleküle können die Oberflächenrekonstruktion verändern. Meistens ordnen sich dabei die Oberflächenatome so um, dass eine energetisch günstige Bindungsgeometrie für das Adsorbat geschaffen wird. Verschiedene Adsorbatatome führen zu verschiedenen Oberflächenstrukturen, so führt die Adsorption von Wasserstoff oder Sauerstoff auf der (001)-Oberfläche von Wolfram, einer Fläche mit quadratisch flächenzentrierter Struktur, zur Erhöhung oder Absenkung der Übergangstemperatur zwischen der nicht rekonstruierten und der (√2,√2)-Wolframoberfläche.[1] Zwischen verschiedenen Rekonstruktionen derselben Oberflächen muss es keine Übergangstemperatur geben, jede Rekonstruktion kann also auch metastabil sein. Bei der gleichen Temperatur können also, abhängig beispielsweise von der Behandlung der Oberfläche, verschiedene Rekonstruktionen derselben Oberfläche vorliegen.
Viele Überstrukturen reiner Oberflächen werden durch Adsorbate aufgehoben. Beispielsweise können die nicht abgesättigten Bindungen von Siliciumoberflächen durch Wasserstoff abgesättigt werden. Die Siliciumatome an der Oberfläche verbinden sich nicht mehr zu Dimeren, dadurch gehen Rekonstruktionen mit Dimerbildungen wieder in Oberflächen ohne dadurch verursachte Überstrukturen über.
Bestimmung der Oberflächenstruktur
Für die Bestimmung der Oberflächenstruktur stehen verschiedene Verfahren zur Verfügung. Direkte Verfahren sind die Vermessung der Oberfläche mit rastermikroskopischen Instrumenten wie dem Rastertunnelmikroskop oder dem Rasterkraftmikroskop in atomarer Auflösung. Diese Verfahren bestimmen die Elektronendichte oder die Höhenlage der Kristallatome direkt. Mit Low-Energy Electron Diffraction (LEED) erhält man Beugungsbilder der Oberfläche, von denen man auf die Struktur der Oberfläche zurückschließen kann. Die Beugungsreflexe einer (2x1)-Überstruktur sind in der einen Richtung halb so weit auseinander, wie man sie von der unrekonstruierten Oberfläche erwarten würde, während sie in der anderen Richtung die erwarteten Abstände haben. Mit LEED kann man also sehr schnell feststellen, dass und in welche Richtungen eine Überstruktur vorliegt.
Typische Rekonstruktionen einiger Oberflächen
Halbleiteroberflächen
Die Oberflächenrekonstruktionen von Halbleiteroberflächen können meistens damit erklärt werden, dass die Anzahl der „abgeschnittenen“ Bindungen (nicht abgesättigte Bindungen, engl. dangling bonds) minimiert werden.
Si(100): Beim (gedanklichen) Durchschneiden eines Siliciumkristalls (Diamantgitter) entlang der (100)-Ebene werden zwei Bindungen je Siliciumatom aufgebrochen. Paare von jeweils benachbarten Siliciumatomen binden mit jeweils einer der abgeschnittenen Bindungen aneinander und bilden sogenannte Dimere.[3] Es bleibt nur mehr eine unabgesättigte Bindung je Siliciumatom. Dabei verzerrt sich das Gitter so, dass jeweils ein Atom im Dimer höher, eines tiefer steht (engl. buckled dimer); unmittelbar benachbarte Dimere sind dabei entgegengesetzt ausgerichtet. Bei Raumtemperatur wechseln die Dimere aber durch thermische Anregungen rasch ihre Ausrichtung und erscheinen im Rastertunnelmikroskop symmetrisch.
Die stabile Oberfläche der Si(111)-Oberfläche hat eine komplexe (7×7)-Rekonstruktion. Die Struktur, das Dimer-Adatom-Stapelfehler-Modell (engl. dimer adatom stacking fault, DAS) wurde 1985 von K. Takayanagi und Mitarbeitern vorgeschlagen,[4] wobei Messungen von Gerd Binnig und Mitarbeitern[5] mit dem Rastertunnelmikroskop eine wichtige Grundlage bildeten.
Metalloberflächen

Bei den Oberflächen reiner Metalle sind Rekonstruktionen weniger häufig als bei Halbleitern; eine Ausnahme bilden die kubisch flächenzentrierten Edelmetalle der 6. Periode, Ir, Pt und Au. Bei diesen drei Metallen rekonstruieren die (100)-Oberflächen und bilden statt des quadratischen Gitters der kubisch flächenzentrierten Struktur eine hexagonal dicht gepackte Atomlage an der Oberfläche aus. Die (110)-Oberflächen dieser Metalle zeigen eine „missing row“-Rekonstruktion; dabei fehlt jede zweite dichtgepackte Atomreihe. Bei Gold rekonstruiert auch die (111)-Oberfläche; die oberste Atomlage ist kontrahiert (Fischgräten-Rekonstruktion, engl. herringbone reconstruction). Diese Rekonstruktionen werden von der besonders niedrigen Oberflächenenergie hexagonal dichter Oberflächen dieser Metalle und einer hohen Zugspannung in der Oberfläche hervorgerufen.
Nichtleiter
Bei Nichtleitern, insbesondere Ionenkristallen und den meisten Oxiden, liegt ein häufiger Grund für die Ausbildung von Oberflächenrekonstruktionen darin, dass Oberflächen makroskopischer Objekte elektrisch weitgehend neutral („ladungskompensiert“) sein müssen.[6] Beispielsweise wäre eine unrekonstruierte (111)-Oberfläche des NaCl-Gitters eine polare Oberfläche, das heißt, dass die oberste Atomlage entweder nur aus positiven oder nur aus negativen Ionen bestünde, was zu einem energetisch ungünstigen, extrem hohen elektrischen Feld führen würde. Dies kann durch eine Rekonstruktion vermieden werden, bei der ein Teil der Ionen in der obersten Atomlage fehlt.
Literatur
- K. Oura, V.G. Lifshits, A.A. Saranin, A.V. Zotov, M. Katayama: Surface Science: An Introduction. Springer-Verlag, Berlin 2003, ISBN 3-540-00545-5.
- Charles Kittel: Einführung in die Festkörperphysik. 14. Auflage. Oldenbourg Wissenschaftsverlag, München 2006, ISBN 3-486-57723-9, S. 532 (eingeschränkte Vorschau in der Google-Buchsuche – Originaltitel: Introduction to Solid State Physics. Übersetzt von Siegfried Hunklinger).
- Andrew Zangwill: Physics at Surfaces. Cambridge University Press, Cambridge 1996, ISBN 0-521-34752-1, S. 207, 258, 259.
Einzelnachweise
- Zangwill: Physics at Surfaces, 1996, S. 259
- Zangwill: Physics at Surfaces, 1996, S. 96
- D. J. Chadi: Atomic and Electronic Structures of Reconstructed Si (100) Surfaces. In: Physical Review Letters. Band 43, Nr. 1, 1979, S. 43–47, doi:10.1103/PhysRevLett.43.43.
- K. Takayanagi, Y. Tanishiro, M. Takahashi, S. Takahashi: Structural-analysis of Si (111)-7×7 by UHV-transmission electron diffraction and microscopy. In: Journal of Vacuum Science & Technology A: Vacuum Surface Films. Band 3, Nr. 3, 1985, S. 1502–1506, doi:10.1116/1.573160.
- G. Binnig, H. Rohrer, Ch. Gerber, E. Weibel: 7 × 7 Reconstruction on Si(111) Resolved in Real Space. In: Physical Review Letters. Band 50, Nr. 2, 1983, S. 120–126, doi:10.1103/PhysRevLett.50.120.
- Jacek Goniakowski, Fabio Finocchi, Claudine Noguera: Polarity of oxide surfaces and nanostructures. In: Reports on Progress in Physics. Band 71, Nr. 1, 2008, S. 016501, doi:10.1088/0034-4885/71/1/016501.