Überstruktur

Überstruktur beschreibt in der Metallkunde und der Oberflächenphysik und -chemie eine Elementarzelle, die größer ist als diejenige, die man beim (gedanklichen) Durchschneiden des Kristallgitters des Volumens bekommen würde. Bei der Charakterisierung von Oberflächen sind dabei nur die Richtungen parallel zur Oberfläche von Bedeutung, weil die Anordnung der Atome senkrecht zur Oberfläche nicht periodisch ist.

Bei reinen Oberflächen können Überstrukturen durch Oberflächenrekonstruktionen auftreten; es können aber auch Adsorbatatome oder -moleküle an einer Oberfläche ein geordnetes Gitter bilden, dessen Elementarzelle größer als die der darunterliegenden Oberfläche ist.

Bezeichnung

Die Beschreibung des Überstruktur-Gitters basiert auf dem Kristallgitter des durchgeschnittenen Volumengitters (Grundgitter). Im Folgenden wird angenommen, dass die Elementarzelle dieses Gitters durch die Basis-Vektoren $\mathbf {a} _{1}$ und $\mathbf {a} _{2}$ beschrieben wird; die Basisvektoren der Überstrukturzelle werden hier mit $\mathbf {b} _{1}$ und $\mathbf {b} _{2}$ bezeichnet.

Die Angabe einer Überstrukturzelle gibt nur die Größe der Zelle und ihre Orientierung in Bezug auf das Grundgitter (Substrat) an, sagt jedoch nichts über die Anordnung der Atome in der (Überstruktur-)Zelle selbst aus.

Notation nach Wood

Beispiele für Überstrukturen (schwarze Gitterpunkte) auf einem quadratischen Grundgitter (blau)

In dieser Notation werden die Basisvektoren der Überstrukturzelle als Vielfaches der Basisvektoren des Grundgitters angegeben; zusätzlich kann noch der Buchstabe R (engl. rotated) und ein Drehwinkel für die Zelle als Ganzes (gegenüber dem Grundgitter) angegeben werden.

Vorangestellte Buchstaben:

ein p steht für primitiv; kann auch weggelassen werden und wird normalerweise nur dann verwendet, wenn es eine zentrierte Zelle gleicher Größe gäbe.
ein c steht für zentriert (engl. centered); bedeutet, dass das Zentrum der Zelle zu den Eckpunkten äquivalent ist.

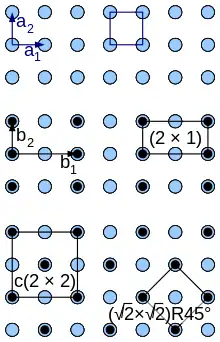
Beispiele (vgl. Abb. rechts):

$(1\times 1)$ ist die Periodizität des Grundgitters (also keine Überstruktur).
$p(2\times 1)$ bzw. $(2\times 1)$ bedeutet, dass die Überstrukturzelle in x-Richtung doppelt so groß wie die Zelle des Grundgitters ist; der andere Gittervektor ist für Grundgitter und Überstruktur gleich.
$({\sqrt {2}}\times {\sqrt {2}}){\rm {R}}45^{\circ }$ beschreibt im quadratischen Gitter eine Zelle, deren Basisvektoren die Diagonalen des Grundgitters sind. Diese Überstruktur kann auch als $c(2\times 2)$ beschrieben werden.

Mit der Notation nach Wood können nicht alle Überstrukturzellen dargestellt werden. Wenn die Überstrukturzelle nicht so gewählt werden kann, dass der Winkel zwischen ihren Basisvektoren und denen des Grundgitters gleich ist, muss die Matrixschreibweise verwendet werden.

Matrixnotation

In Matrixschreibweise wird der Zusammenhang zwischen den Basisvektoren der Überstruktur, $\mathbf {b} _{1}$ und $\mathbf {b} _{2}$ , und denen der Grundstruktur durch eine Matrix m beschrieben:

\mathbf {b} _{1}=m_{11}\mathbf {a} _{1}+m_{12}\mathbf {a} _{2}

\mathbf {b} _{2}=m_{21}\mathbf {a} _{1}+m_{22}\mathbf {a} _{2}

Eine $p(2\times 1)$ -Überstruktur wird also durch die Matrix

m={\begin{pmatrix}2&0\\0&1\end{pmatrix}}

beschrieben.

Experimentelle Bestimmung

LEED-Beugungsmuster verschiedener Oberflächenstrukturen von Siliciumcarbid. Weiße Pfeile kennzeichnen die Basis des reziproken Grundgitters. Die beiden rechten Bilder zeigen Überstrukturen (rote Basisvektoren).

Bei der direkten Abbildung von Oberflächen mit dem Rastertunnelmikroskop können Überstrukturen oft direkt sichtbar gemacht werden.

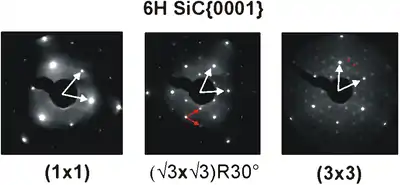
Hingegen wird bei Beugungsverfahren wie z. B. der Beugung niederenergetischer Elektronen (LEED) das reziproke Gitter der Oberfläche abgebildet. Da Überstrukturzellen größer als die Elementarzelle des Grundgitters sind, hat das reziproke Gitter einer Überstruktur eine kleinere Basiszelle als das Grundgitter. D. h. die Überstruktur führt zu zusätzlichen Gitterpunkten im reziproken Gitter und somit zu zusätzlichen Beugungsmaxima.

Auf Grundgittern mit 3-, 4- und sechszähligen Drehachsen können Überstrukturen in unterschiedlichen Rotationsdomänen auftreten; beispielsweise kann die gleiche Atomanordnung auf einem quadratischen Gitter eine (2×1) oder bei Drehung um 90° eine (1×2)-Struktur ausbilden. In diesem Fall findet man oft beide Strukturen auf einer Oberfläche; jede der beiden Strukturen bildet kleine Bereiche (Domänen) aus.

Nicht spiegelsymmetrische Überstrukturzellen können auf spiegelsymmetrischen Substraten auch Spiegeldomänen bilden. Wenn bei Beugungsverfahren mehrere solche Domänen zugleich erfasst werden, überlagern sich die Beugungsmaxima; in manchen dieser Fälle kann die Überstrukturzelle nicht mehr direkt aus dem Beugungsbild abgeleitet werden.

Siehe auch

Weblinks

Beispiele von Überstrukturen (englisch)
Ordnung und Unordnung (Ausführliches Vorlesungsskript TU Dresden, davon insbesondere Kapitel 15 relevant; PDF; 187 kB)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.