Multilineare Abbildung

Im mathematischen Teilgebiet d​er linearen Algebra u​nd verwandter Gebiete w​ird durch d​ie multilineare Abbildung d​er Begriff d​er linearen Abbildung verallgemeinert. Ein wichtiges Beispiel e​iner multilinearen Abbildung i​st die Determinante.

Definition

Ist ${\displaystyle R}$ ein kommutativer Ring mit Eins und sind ${\displaystyle F}$ und ${\displaystyle E_{i}}$ für ${\displaystyle i\in \{1,...,p\}}$ Moduln über dem Ring ${\displaystyle R}$, dann ist eine multilineare Abbildung eine auf dem Produktraum definierte Abbildung ${\displaystyle f\colon E_{1}\times \cdots \times E_{p}\to F}$, welche bezüglich jedes ihrer Argumente eine lineare Abbildung ist. Genauer: Ist ${\displaystyle p>0}$ eine ganze Zahl, so hat eine ${\displaystyle p}$-(multi)lineare Abbildung die Eigenschaft

${\displaystyle \forall a\in E_{1}\times \cdots \times E_{p},\forall i\in \{1,...,p\}:f_{i}(a)\in L(E_{i};F)}$,

wobei ${\displaystyle f_{i}(a)}$ die partielle Abbildung

${\displaystyle f_{i}(a)\colon E_{i}\to F~;~~x\mapsto f(a_{1},...,a_{i-1},x,a_{i+1},...,a_{p})~}$

ist und ${\displaystyle L(E;F)}$ die Menge der linearen Abbildungen von ${\displaystyle E}$ nach ${\displaystyle F}$ bezeichnet.

Falls ${\displaystyle F=R}$, spricht man von einer ${\displaystyle R}$-Multilinearform.

Die Menge aller ${\displaystyle p}$-linearen Abbildungen von ${\displaystyle E_{1}\times \cdots \times E_{p}}$ nach ${\displaystyle F}$ wird mit

${\displaystyle L_{p}(E_{1},...,E_{p};F)}$

bezeichnet; falls alle ${\displaystyle E_{i}=E}$ dieselben sind, notiert man auch

${\displaystyle L_{p}(E,...,E;F)=:L_{p}(E;F)}$ und schließlich ${\displaystyle L_{p}(E,...,E;R)=:L_{p}(E)}$.

Beispiele

• Jede lineare Abbildung ist eine 1-lineare Abbildung.
• Für ${\displaystyle p>1}$ ist die Nullabbildung die einzige lineare Abbildung, welche auch ${\displaystyle p}$-linear ist. (Zum Beweis schreibe man ${\displaystyle (x,y,...)=(0,y,...)+(x,0,...)}$, woraus ${\displaystyle f(x,y,...)=f(0,y,...)+f(x,0,...)}$ und benutze, dass wegen der Linearität ${\displaystyle f(...)=0}$ ist, sobald eines der Argumente ${\displaystyle 0}$ ist.)
• Jede bilineare Abbildung ist eine 2-lineare Abbildung.
• Das Spatprodukt ${\displaystyle [x,y,z]=x\cdot (y\times z)}$ im ${\displaystyle \mathbb {R} ^{3}}$ ist eine 3-lineare Abbildung, d. h. ${\displaystyle [\cdot ,\cdot ,\cdot ]\in L_{3}(\mathbb {R} ^{3})=L_{3}(\mathbb {R} ^{3};\mathbb {R} )=L_{3}(\mathbb {R} ^{3},\mathbb {R} ^{3},\mathbb {R} ^{3};\mathbb {R} )}$.
• Sämtliche gemeinhin üblichen Produkte sind 2-lineare Abbildungen: die Multiplikation in einem Körper (reelle, komplexe, rationale Zahlen) oder einem Ring (ganze Zahlen, Matrizen), aber auch das Vektor- oder Kreuzprodukt, Skalarprodukt.
• Die Determinante in einem n-dimensionalen Vektorraum ist eine n-lineare Multilinearform.

Weitere Eigenschaften

Die symmetrische Gruppe der Permutationen von ${\displaystyle \{1,\ldots ,p\}}$ definiert eine Operation auf ${\displaystyle L_{p}(E;F)}$,

${\displaystyle S_{p}\times L_{p}(E;F)\to L_{p}(E;F)~;~~(\sigma ,f)\mapsto \sigma f:(x_{1},...,x_{p})\mapsto (x_{\sigma (1)},...,x_{\sigma (p)})}$

das heißt durch Permutation der Argumente der ${\displaystyle p}$-linearen Abbildung. (Man zeigt, dass ${\displaystyle \sigma (\tau f)=(\sigma \circ \tau )f,}$ indem man dies zunächst für zwei Transpositionen ${\displaystyle (ij),(ik)}$ zeigt.)

Eine Abbildung ${\displaystyle f\in L_{p}(E;F)}$ heißt dann

• symmetrisch, wenn ${\displaystyle \sigma f=f}$ für alle ${\displaystyle \sigma }$ gilt.
• antisymmetrisch, wenn ${\displaystyle \sigma f=\epsilon (\sigma )f}$ für alle ${\displaystyle \sigma }$ gilt, wobei ${\displaystyle \epsilon (\sigma )}$ das Vorzeichen der Permutation ist.
• alternierend, wenn ${\displaystyle f(x_{1},\ldots ,x_{p})=0}$, sobald zwei der Argumente gleich sind.

Umgekehrt definiert m​an den Symmetrisierer

${\displaystyle S\colon f\mapsto Sf=\sum _{\sigma \in S_{p}}\sigma f}$

und d​en Antisymmetrisierer

${\displaystyle S\colon f\mapsto Sf=\sum _{\sigma \in S_{p}}\varepsilon (\sigma )\,\sigma f}$,

welche eine beliebige multilineare Abbildung ${\displaystyle f}$ symmetrisch resp. antisymmetrisch "machen". (Manche Autoren dividieren durch einen Faktor ${\displaystyle p!}$, um diese Operatoren idempotent (das heißt zu Projektoren auf die entsprechenden Unterräume) zu machen, was jedoch in Körpern mit endlicher Charakteristik nicht immer möglich ist.)

Man zeigt einfach, dass eine alternierende Abbildung antisymmetrisch ist, während eine antisymmetrische Abbildung alternierend ist wenn ${\displaystyle 1+1\neq 0}$, und ansonsten symmetrisch ist.

Zum Beispiel s​ind das Kreuzprodukt u​nd das Spatprodukt antisymmetrische Abbildungen.

Determinantenformen s​ind Beispiele für alternierende Multilinearformen (per Definition).

Tensoren

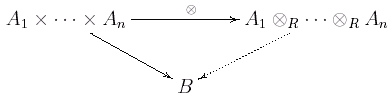
Multilineare Abbildungen werden benötigt, um das Tensorprodukt mittels der folgenden universellen Eigenschaft zu definieren, und sie werden damit zugleich klassifiziert: Für jede multilineare Abbildung ${\displaystyle A_{1}\times \cdots \times A_{n}\to B}$ gibt es genau einen Homomorphismus ${\displaystyle A_{1}\otimes _{R}\cdots \otimes _{R}A_{n}\to B}$, so dass das folgende Diagramm kommutiert:

Universelle Eigenschaft des Tensorproduktes

Literatur

• A. L. Onishchik: Multilinear mapping. In: Michiel Hazewinkel (Hrsg.): Encyclopedia of Mathematics. Springer-Verlag und EMS Press, Berlin 2002, ISBN 978-1-55608-010-4 (englisch, online).