Coandă-Effekt
Mit dem Sammelbegriff Coandă-Effekt werden verschiedene ursächlich nicht zusammenhängende Phänomene bezeichnet, die eine Tendenz eines Gasstrahls oder einer Flüssigkeitsströmung nahelegen, an einer konvexen Oberfläche „entlangzulaufen“, anstatt sich abzulösen und sich in der ursprünglichen Fließrichtung weiterzubewegen.

Eine genaue Definition und die Abgrenzung zum Bernoulli-Effekt sind schwierig. In der wissenschaftlichen Literatur wird der Begriff selten verwendet.
Geschichte
Henri Coandă baute 1910 sein erstes Flugzeug, die Coandă-1910. Es sollte mit einem Thermojet, einer Kombination aus kolbenmotorgetriebenem Verdichter und zwei Brennkammern, angetrieben werden. Der Motor war an der Rumpfspitze angebracht und sollte die beiden Schubstrahlen schräg nach hinten/außen ausstoßen. Bei der ersten Erprobung beobachtete Coandă jedoch, dass die heißen Gase der Rumpfkontur folgten und daran entlangströmten. Das Flugzeug wurde bei diesen Arbeiten zerstört, weitere praktische Versuche mit Strahlantrieben erfolgten erst etwa 30 Jahre später.
Der Coandă-Effekt wurde auch zur Projektierung von „Fliegenden Untertassen“ wie dem Avrocar verwendet. Heute gibt es technische Anwendungen des Effektes in der Luftfahrt, Formel 1 und anderen Bereichen.
Flüssigkeitsströmungen

Das Haften der Flüssigkeit an umströmten Festkörpern ist auf die molekularen Wechselwirkungen wie die Van-der-Waals-Wechselwirkung zurückzuführen. Diese bewirken das Haften von Flüssigkeiten auch an der Unterseite von waagerechten Flächen. Die Umlenkung des Wasserstrahls ist daher hier nicht auf den Coandă-Effekt zurückzuführen, der auf einer Wechselwirkung des Fluidstrahls mit dem umgebenden Fluid im Zusammenhang mit einer benachbarten Oberfläche beruht.
Gasstrahlen
Bei einer „beweglichen“ Oberfläche kann man umgekehrt auch zeigen, wie sie sich an einen Gasstrahl „hängt“. Das folgende einfache Experiment zeigt dies:
- Blase an der (konvexen) Oberseite eines Blattes Papier entlang. Es wird angehoben, „klebt“ am Luftstrahl und wird in der Schwebe gehalten. Da das Papier nur ein geringes Gewicht hat, stellt sich ein Gleichgewicht ein: Die Wand ist beweglich, kann also der Ablenkung der Strömung „nachgeben“, und die Strömung wird nur geringfügig abgelenkt – nur so viel, wie zur Überwindung des Papiergewichtes erforderlich ist.
Das Experiment ist sehr einfach auszuführen und wird fälschlicherweise gern zur Erklärung des Auftriebes an Tragflächen herangezogen. Es erklärt jedoch nicht die Entstehung des Auftriebes an Tragflächen, denn diese werden anders umströmt.
Ein Nebeneffekt ist der Ping-Pong-Ball, der in einem schrägen Luftstrahl „hängt“: Durch den Coandă-Effekt löst sich die Strömung des Luftstrahles nicht vom Ball ab, sondern umrundet ihn (fast) völlig ohne Ablösung. Da der Ball leicht unterhalb des Zentrums des Luftstrahles hängt, erfolgt die Umströmung nicht symmetrisch. Es wird mehr Luft nach unten abgelenkt, da an der Unterseite des Balles die Strömungsgeschwindigkeit und der Strahlquerschnitt gegenüber der Oberseite geringer ist. Als Reaktion erfährt der Ball eine Kraft nach oben. Dies erfolgt in Überlagerung mit dem Magnus-Effekt (der Ball dreht sich). Beide Effekte – jeder für sich – lassen den Ball nicht nach unten fallen, sondern nur an der Unterseite des Luftstrahles entlang„rutschen“. Der Widerstand, den der Ball der Strömung entgegensetzt, hält ihn auf Distanz zur Düse, und die Schwerkraft verhindert, dass er einfach weggeblasen wird. So kann der Ball in einer mehr oder weniger stabilen Position schweben.
Erklärung
Coandă beschrieb Folgendes: Ein Gas-Strahl – also eine räumlich eng begrenzte Strömung, die sich von der (meist ruhenden) Umgebung deutlich unterscheidet – fließt an einer Fläche entlang. Wenn die Fläche gegenüber der ursprünglichen Strömungsrichtung zurückweicht, fließt der Strahl dabei nicht geradeaus weiter, sondern folgt der Fläche. Coandă hatte vor dieser Beobachtung bereits umfangreiche Versuche mit „normalen“ Strömungen (also nicht mit Strahlen) unternommen und war sich sicherlich klar darüber, dass normale Strömungen einer konvexen Rundung nur begrenzt folgen können und sich dann ablösen.
Es soll hier eine Strömung entsprechend dem Coandă-Effekt (im Folgenden nur hier der Kürze halber als „Coandă-Strömung“ bezeichnet) mit einer normalen Strömung beispielsweise an einem Tragflächenprofil kurz verglichen werden. Auffallend ist die deutlich größere Fähigkeit der Coandă-Strömung, einer konvexen Wand zu folgen und sich nicht abzulösen. Daher ist es sinnvoll, neben den Gemeinsamkeiten vor allem die Unterschiede zwischen Coandă- und normaler Strömung herauszuarbeiten.
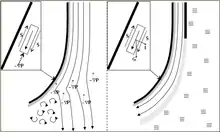
Beide Strömungsarten bestehen in Wandnähe aus einer sehr dünnen Reibungs-Grenzschicht (in der Grafik dunkelgrau) und weiter außerhalb aus einer von der Wandreibung unbeeinflussten Strömung. In der Grenzschicht entscheidet sich, unter welchen Bedingungen die Strömung entlang der Wand in unmittelbarer Wandnähe zum Stillstand kommt und dann folglich die Wand verlassen kann (siehe Strömungsabriss).
In einer normalen Strömung gilt außerhalb der Grenzschicht Bernoullis Gesetz. Es ist hier wie folgt anzuwenden: Konvexe zurückweichende Wand → mehr Platz für die Strömung → Verlangsamung der Strömung aufgrund des Massenerhaltungsgesetzes → Druckanstieg aufgrund Bernoullis Gesetz. In der Grafik ist der Druckgradient in seiner bremsenden Wirkung – also negativ – skizziert (). In der Grenzschicht wird der Druckanstieg von der ungestörten Strömung bis zur Wand unverändert weitergegeben, dort wird also die Strömung nicht nur durch die Reibung, sondern auch noch durch den Druckanstieg abgebremst, was sehr bald zum Stillstand und zur Ablösung führt.
Der wesentliche Unterschied zur Coandă-Strömung liegt in der Tatsache, dass dort ein Strahl die Wand entlang strömt („Wandstrahleffekt“). Die Coandă-Strömung besteht also aus der Grenzschicht, einer relativ dünnen ungestörten Schicht (dem Strahl), dann aber aus einer weiteren Reibungsschicht zu den Luftmassen „außen“ (in der Grafik hellgrau skizziert). Die Luft außen befindet sich in Ruhe, deshalb gibt es auch keinen Druckanstieg entsprechend dem Bernoulli-Gesetz, in der Grenzschicht zur Wand fehlt also eine wesentliche Ursache für die Ablösung. Die Coandă-Strömung haftet also länger als eine normale Strömung. Was letztendlich zur Ablösung einer Coandă-Strömung führt, ist die Reibung ( shear stress), die Zentrifugalkraft (, in der normalen Strömung meistens nicht bedeutend) und in entsprechenden Fällen auch die Schwerkraft .
Da im normalen Flugbetrieb nicht ein Strahl die Tragflächen entlang strömt, sondern eine normale Strömung, in der außerhalb der Grenzschicht überall Bernoullis Gesetz gilt und Druckanstieg produziert wird, kann die Coandă-Strömung nicht zur Erklärung der Auftriebsentstehung herangezogen werden.
Umstände, die dem Verständnis des Coandă-Effektes entgegenstehen:
- Die Coandă-Strömung wird schwerer verständlich im dreidimensionalen Raum, weil die Ablösung nicht nur durch Stillstand („von hinten“) hervorgerufen wird, sondern auch an den Seiten des Strahles durch Querbeschleunigung erfolgt, der Strahl wird schmaler und dicker.
- Schwerst durchschaubar wird der Coandă-Effekt, wenn er in verschiedensten Experimenten gemeinsam mit anderen Effekten wirkt, wie im oben angegebenen Ping-Pong-Ball-Experiment, in dem auch der Magnus-Effekt die Ablösung weiter verzögert.
Anwendungen
Der Coandă-Effekt wird im Flugzeugbau zur Erhöhung des Auftriebes in zwei Varianten eingesetzt:
Das Triebwerk wird knapp über dem Tragflügel angeordnet und dessen Schubstrahl durch ein Klappensystem am Tragflügel „saugend“ nach unten abgelenkt – dies ist naturgemäß nur in einem sehr kleinen Bereich des Tragflügels möglich, der Rest des Flügels arbeitet in einer „normalen“ Strömung. Eine seiner ersten Anwendungen fand der Effekt bei der sowjetischen Antonow An-32, Antonow An-72, Antonow An-74 und bei einem Bewerber des „AMST-Projekts“ der US Air Force (Advanced Medium STOL Transport), der YC-14. Wenn diese Anordnung Nutzen bringen soll, erfordert sie gewaltige Triebwerksleistungen, auch müssen die Tragflügelklappen im Bereich des Schubstrahles besonders kräftig gebaut und geschützt werden. Ebenso gibt es große Probleme bei der Steuerbarkeit und Sicherheit (beispielsweise bei Triebwerksausfall).
Die zweite Anwendung ist eine Mischung aus Coandă- und „normaler“ Strömung: Der Strahl wird in die bereits kräftig ausgebildete Grenzschicht einer „normalen“ Strömung geblasen, um sie weiter um Klappen etc. fließen zu lassen, als es sonst möglich wäre. Dies ist keine „reine Coandă-Strömung“ mehr, denn die Strömung in der Umgebung soll nur „verbessert“ werden: An der äußeren Scherschicht soll die hohe Geschwindigkeit des Strahles an die schon langsame Grenzschicht der äußeren Strömung übertragen werden.
Erfolgreiche Anwendungen dieses Prinzips gibt es an konventionellen Tragflügeln im Bereich von Nasen- und Endklappen (Grenzschicht-Ausblasung), zum Beispiel bei den großen von der japanischen Marine und Küstenwache eingesetzten Flugbooten des Herstellers Shin Meiwa. Auch diese Anwendung erfordert sehr hohe Triebwerksleistungen, denn die kräftigen Strahlen müssen ja erzeugt werden. Die „normale“ Strömung kann mit solchen Maßnahmen in besonderen Flugzuständen (Langsamflug bei Start und Landung) verbessert werden, ein normaler Flugzustand ist damit aber aus Kostengründen nicht beeinflussbar.
Eine spektakuläre Anwendung ist der NOTAR-Hubschrauber, an dem der Heckrotor eingespart werden kann: Am als Rohr ausgeführten runden Ausleger wird im Bereich des Rotor-Abwindes durch Ausblasen von Luft der Abwind so um den Ausleger herumgeleitet, dass er das Rotor-Gegendrehmoment teilweise ausgleicht. Zusätzlich wird aber noch eine variable Steuerdüse am Ende des Auslegers benötigt. Die Vorteile liegen in der Einsparung schwerer und komplexer Mechanik und im erheblichen Sicherheitsgewinn. Der Preis: Ein zusätzliches innenliegendes Gebläse zur Erzeugung des Luftstromes am Heckausleger. Ein ausgeführtes Muster ist der MD Explorer.
Im Jahre 2012 hat dieses Prinzip auch in der Formel 1 Einzug gehalten: Die Auspuffsysteme nutzen diesen Effekt, um mehr Anpressdruck zu erzeugen,[1] indem die Auspuffgase auf die Spalte zwischen Hinterrädern und Bodenplatte geführt werden und damit den Diffusor gegen seitliche Einströmungen abschirmen.
Weitere Anwendungen gibt es im Heizungs- und Lüftungsbau sowie im Küchen- und Laborbereich. Tropffreies Ausgießen von Flüssigkeit – besonders aus einem hoch gefüllten Becherglas (mit Ausguss) – erfolgt entlang eines angelegten Glasstabs. Ausgießer gibt es an Getränkekannen und für Getränkepackungen und (Alkoholika-)Flaschen. Alte Korkstöpselflaschen aus der Drogerie hatten einen ausgießgünstigen Kragen, Medizin- und Laborglasflaschen haben meist Ausgießringe aus Kunststoff oder aber auch aus dem Glasrand selbst gebildete. Die lange Liste von Coandăs US-Patenten enthält unter anderem auch Düsen für Vergaser.
In Wasserfassungen nutzen wartungsfreie Filter den Coandă-Effekt über schräggestellte Einlaufsiebe[2].
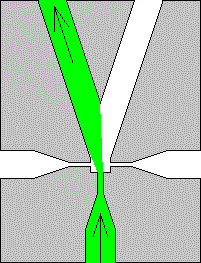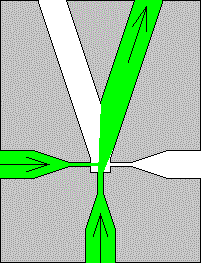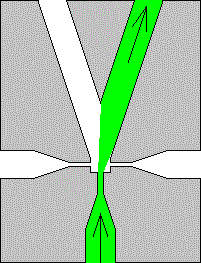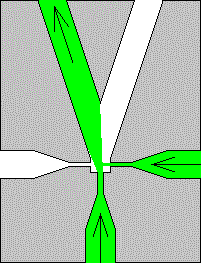
Der Coandă-Effekt wird auch für pneumatische oder hydraulische Steuerungssysteme genutzt. (Fluidik)
Literatur
- Alexander Sauberer: Experimentelle Studien zum Coanda-Effekt. Dipl.-Arb., TU Wien 1998.
- Anton Felder: Untersuchungen zum Coanda-Effekt-mögliche Anwendung im Bauingenieurwesen. Diss., TU München 1993.
- Heribert Martinides: Messungen des turbulenten Freistrahls und des Coanda-Effektes. Dipl.-Arb., TU Wien 1958.
Weblinks
Quellen
- Formel 1 Auspuff-Vergleich: Ein Problem namens Coanda der Zeitschrift AUTO MOTOR UND SPORT
- Wartungsfreie Feinsiebe in Inox – Thaler-System