Kowalewskaja-Kreisel

Der Kowalewskaja-Kreisel ist in der Kreiseltheorie einer der drei Kreiseltypen, deren Bewegungsgleichungen bei beliebigen Anfangsbedingungen analytisch gelöst werden können. Er ist ein schwerer symmetrischer Kreisel, dessen drei Hauptträgheitsmomente A, B und C die Bedingung A = B = 2C erfüllen, und dessen Massenmittelpunkt in der Ebene liegt, die von den zu A und B gehörenden Hauptachsen aufgespannt wird.

Sofja Wassiljewna Kowalewskaja gab die Entdeckung des Kreisels 1888 in einer preisgekrönten Arbeit über die Rotation eines Starrkörpers um einen Fixpunkt[1] und gleich auch die Lösung der Euler-Poisson-Gleichungen bekannt. Für die Darstellung der Lösungsfunktionen benötigte Kowalewskaja etwa 50 Seiten, was die Komplexität der Bewegungsmöglichkeiten des Kreisels unterstreicht. Die Vereinfachung der Lösung und die Klassifizierung der Bewegungsmodi ist so aufwändig, dass sie die Wissenschaft noch bis ins 21. Jahrhundert beschäftigten[2].

Die Kowalewskaja-Konstante K = k² verschwindet für Staude-Drehungen, siehe die Animationen in Abb. 3 und 4. Das Bifurkationsdiagramm des Kowalewskaja-Kreisels ist durchsetzt mit Separatrizen, die Phasen, wo gleichartige, topologisch verwandte Bewegungstypen auftreten, voneinander trennen, siehe Abb. 5. Eine typische Bewegung des Kowalewskaja-Kreisels weist im körperfesten Raum der Drehimpulse Trajektorien auf, die einen ringförmigen Schlauch umlaufen und ihn dabei dicht ausfüllen, siehe Abb. 6a-d. Die Separatrizen sind die Phasengrenzen, in deren Zentren eine instabile periodische Bahn liegt. In fast allen Phasen durchläuft der Kreisel Gebiete stabilen und instabilen Verhaltens. Diese Tatsache kann mit Fomenko-Graphen skizziert werden, siehe Abb. 7. Poincaré-Schnitte sind eine weitere Möglichkeit das Verhalten zu veranschaulichen, indem wie in einer Landkarte die stabilen Bereiche eingefärbt werden, an deren Grenzen die Separatrizen liegen, siehe Abb. 8.

Der Kowalewskaja-Kreisel ist von kreiseltheoretischer Bedeutung und kann zur Modellierung gewisser Phänomene in stationären Strömungen inkompressibler Flüssigkeiten verwendet werden; eine technische Anwendung gibt es jedoch Anfang des 21. Jahrhunderts noch nicht.[3]

Realisierungen

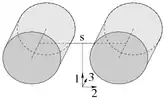Abb. 1: Realisierung nach Schwarz
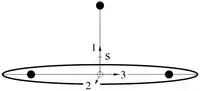Abb. 2: Realisierung nach Richter

Das Trägheitsellipsoid des Kowalewskaja-Kreisels ist rotationssymmetrisch aber der Massenmittelpunkt befindet sich nicht auf der Symmetrieachse. Das ist nur bei inhomogener Massenverteilung möglich[4]. Auf Hermann Schwarz geht eine Konstruktion mit zwei Zylindern zurück[5] und P. H. Richter benutzte die Form mit einem Kreisring und drei Massenpunkten[6], die auch in den Animationen unten verwendet wurde. In den Abbildungen 1 und 2 bezeichnet s den Massenmittelpunkt und das Koordinatenkreuz den Stützpunkt.

Phänomenologie

Karussell-Bewegungen

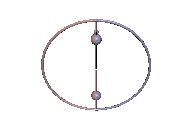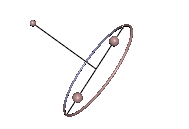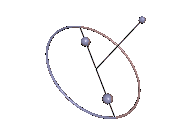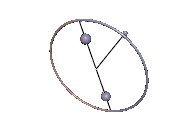Abb. 3: Stabile Karussell-Bewegung
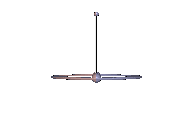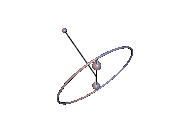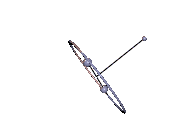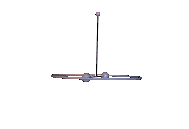Abb. 4: Instabile Karussell-Bewegung

Die Karussell-Bewegungen sind Staude-Drehungen des Kowalewskaja-Kreisels, bei denen der Kreisel um eine lotrechte Achse rotiert, die mit keiner der Hauptträgheitsachsen übereinstimmt. In Abb. 3 tut er das in stabiler Weise und in Abb. 4 ist der Schwerpunkt zu hoch und die Karussell-Bewegung wird instabil. In beiden Animationen wurde der Neigungswinkel zwischen der 1-Achse und der Lotlinie um 0,01 rad gegenüber dem anfänglichen Sollwert erhöht, was in Abb. 3 unbemerkt bleibt, in Abb. 4 jedoch zum periodischen Ausbrechen des Kreisels führt.

Karussell-Bewegungen entstehen unter den Bedingungen

n₂ = q = p² + c n₁ = k = 0.

siehe #Gleichgewichtslösungen.

Bifurkationsdiagramm des Kowalewskaja-Kreisels

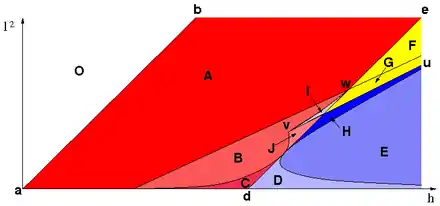
Abb. 5: Bifurkationsdiagramm des Kowalewskaja-Kreisels (schematisch)

Einen Eindruck von der Komplexität des Verhaltens des Kowalewskaja-Kreisels vermittelt das Bifurkationsdiagramm in Abb. 5. Bifurkation (Verzweigung) ist das Phänomen, das ein System an einem kritischen Punkt in verschiedene Zustände verzweigen kann. So kann ein lotrecht stehender Stab bei kleiner Störung nach links oder rechts umfallen sofern er irgendwie an eine Ebene gebunden ist. Die Trennlinie zwischen den beiden Pfaden ist eine Separatrix, von der auch beim unsymmetrischen Euler-Kreisel eine existiert. Die Bewegungen entlang der Separatrizen sind oft instabil.

Die kritischen Punkte beim Kowalewskaja-Kreisel stellen sich bei bestimmten Werten der Gesamtenergie h und des vertikalen Drehimpulses l ein. Das Bifurkationsdiagramm wird durch die #Gleichgewichtslösungen in fünf Flächen geteilt, wobei in der weißen Fläche O unphysikalische Parameterkombinationen auftreten, die dem Kreisel verboten sind. Die eingefärbten Bereiche sind dem Kreisel zugänglich und er zeigt in den roten, gelben, blauen und grauen Gebieten jeweils topologisch ähnliches Verhalten.

Der linke Rand a–b definiert den lotrecht hängenden Kreisel, dessen Bewegung immer stabil ist, und die Linie d–e den lotrecht aufrechten Kreisel, dessen Bewegung immer instabil ist. Charakteristisch für den Kowalewskaja-Kreisel sind die Karussell-Bewegungen, die auf der Linie u-v-w stattfinden und die auf der Linie u–v stabil und im Bereich v–w instabil sind[7], siehe Abb. 3 und 4. Entlang der zusätzlich eingezeichneten Linien verzweigen die periodischen Orbits, die der Kreisel beim minimalen oder maximalen Wert der Kowalewskaja-Konstante verfolgt, siehe Abb. 7.

An den im Bifurkationsdiagramm eingezeichneten Linien finden Bifurkationen statt:

A–F, C–D, G–H: Bifurkation der Energiefläche
A–B, F–G: elliptische Pitchfork-Bifurkation
D–E: hyperbolische Pitchfork-Bifurkation
B–C, B–J: Tangenten Bifurkation
E–H: hyperbolische Periodenverdoppelungsbifurkation

In den Gebieten dazwischen sind die Energieflächen einheitlich geblättert.

Bifurkation	Darstellung	Kowalewskaja- Konstante	Definitionsbereich
Analytische Form des Bifurkationsdiagramms
Die Tabelle gibt die analytischen Darstellungen der Phasengrenzen in Abb. 5 für c = 1.
a–b	l = 2p, h = p² - 1	k² = ( p² + 1 )²	p > 0
d–e	l = -2p, h = p² + 1	k² = ( p² - 1 )²	p > 0
u–v	l = -p³ - p^–1, h = ³⁄₂ p² + ¹⁄₂ p^–2	k² = 0	0 < p < 3^–0,25
v–w	l = -p³ - p^–1, h = ³⁄₂ p² + ¹⁄₂ p^–2	k² = 0	3^–0,25 < p < 1
B–C, B–J	l² = ¹⁶⁄₂₇ h³	k² = 1 - h²/3	0 < h < √3
A–B, F–G	l² = 2h	k² = 0	h > 0
E-D, E–H	l² = h ± √(h² - 2)	k² = l^–4	h > √2

Familien gleicher Tori

Abb. 6a: Trajektorien (Netz bildende Linien) und Torus (bräunlich schattiert) im Drehimpulsraum.
Abb. 6b: Separatrix mit instabilem periodischem Orbit (grau) im Zentrum
Abb. 6c: Andere Seite derselben Separatrix mit zwei zueinander symmetrischen Tori (grün).
Abb. 6d: Tori bei kleinerer Kowalewskaja-Konstante gehen in stabile periodische Bahnen (grau) über.

Bei einer gegebenen Bewegung des Kowalewskaja-Kreisels sind die Gesamtenergie, der Drehimpuls in Lotrichtung und die Kowalewskaja-Konstante unveränderlich. Weil der Kowalewskaja-Kreisel ein integrables System darstellt, bewegt sich der Drehimpuls im körperfesten Hauptachsensystem auf einem ringförmigen Schlauch oder Torus und die Trajektorien füllen diesen dicht aus[8], siehe Abb. 6a. Der Torus kann sich dabei selbst durchdringen, die Außenseite ist heller als die Innenseite getönt. Bei gleicher Gesamtenergie und gleichem Drehimpuls in Lotrichtung verändern sich die Tori stetig mit der Kowalewskaja-Konstante und bilden eine Familie, was die Farbgebung andeuten soll. An einem Verzweigungspunkt, gehen die Tori in andere Familien über. Der Verzweigungspunkt ist eine Separatrix, die diesen angrenzenden Torifamilien gemeinsam ist, Abb. 6b und c. Im gezeigten Fall aus dem Gebiet B treffen in der Separatrix ein roter und zwei zueinander symmetrische grüne Tori zusammen. Im Zentrum der Separatrix liegt ein instabiler periodischer Orbit, den der Kreisel bei geringster Störung entlang der Separatrix verlässt, wobei er in einen der benachbarten Tori verzweigt. Nimmt die Kowalewskaja-Konstante zu oder ab, kann der Kreisel auf einen weiteren Verzweigungspunkt treffen, oder bei einem extremalen Wert der Konstanten in einem stabilen periodischen Orbit enden, wie dem grauen in Abb. 6d. Mit ansteigender Kowalewskaja-Konstante durchläuft der Kreisel in den Gebieten A bis J immer in gleicher Weise stabile Orbits, zwischen denen Separatrizen liegen. Das lässt sich mit Fomenko-Graphen versinnbildlichen.

Fomenko-Graphen

Abb. 7: Fomenko-Graphen

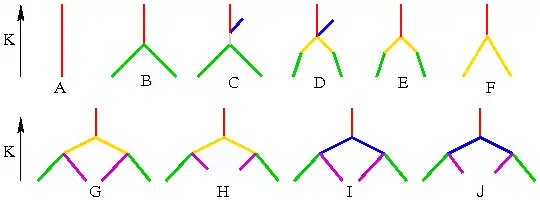
Die Abfolge der Bifurkationen bei zunehmender Kowalewskaja-Konstante lassen sich in Fomenko-Graphen darstellen, die in den Gebieten A bis J jeweils gleich geartet sind. In den freien Enden der Äste der Graphen finden stabile Bewegungen statt. Wo Äste verschiedener Farben aufeinander treffen findet eine Bifurkation entlang von Separatrizen statt. Die verschiedenen Farben gruppieren Bewegungstypen. Entlang der lila Äste beispielsweise finden karussellartige Bewegungen statt[9].

Poincaré-Schnitte

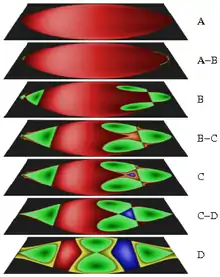
Abb. 8: Poincare-Schnitte entlang eines Pfades D-C-B-A im Bifurkationsdiagramm

Einen anschaulichen Eindruck vermitteln die Poincaré-Schnitte, siehe Abb. 8. Eine Trajektorie füllt im Phasenraum der Drehimpulse einen ringförmigen Schlauch, einen Torus, dicht aus. Die Tori werden durch die Kowalewskaja-Konstante k charakterisiert. Bei einem kritischen Wert von k entarten die Tori zu einer Separatrix, die einer instabilen periodischen Bahn entspricht.

Die Trajektorien des Kreisels werden mit einer Kugel verschnitten, die Oberfläche dieser Kugel gemäß der Familie der geschnittenen Tori eingefärbt und in die Ebene projiziert. Die Farben entsprechen den Familien der Tori und die Helligkeit wächst mit k. Die stabilen Orbits sind die hellen und dunklen Zentren der Flächen. Die Flächen werden durch Separatrizen getrennt, an denen deutliche Farbsprünge auftreten. Die Schnittpunkte von Separatrizen sind instabile periodische Orbits.

Zwischen D und C findet eine Bifurkation der Energiefläche statt und der gelbe Bereich verschwindet. Zwischen C und B verschwindet blau in einer Tangenten-Bifurkation. Zwischen B und A verschwindet grün in einer Pitchfork-Bifurkation[10].

Lösung der Bewegungsgleichungen

Euler-Poisson-Gleichungen

Aus Symmetriegründen kann die zu A gehörende erste Hauptträgheitsachse so gewählt werden, dass der Massenmittelpunkt des Kreisels auf ihr liegt. Damit spezialisieren sich die Euler-Poisson-Gleichungen beim Kowalewskaja-Kreisel zu[11]

{\begin{aligned}2{\dot {p}}=&qr\\2{\dot {q}}=&-rp-c\,n_{3}\\{\dot {r}}=&c\,n_{2}\\{\dot {n}}_{1}=&rn_{2}-qn_{3}\\{\dot {n}}_{2}=&pn_{3}-rn_{1}\\{\dot {n}}_{3}=&qn_{1}-pn_{2}\end{aligned}}

Darin stehen p, q, r = ω_1,2,3 für die Winkelgeschwindigkeiten, der Vektor ${\hat {n}}=-{\hat {e}}_{z}=n_{1}{\hat {e}}_{1}+n_{2}{\hat {e}}_{2}+n_{3}{\hat {e}}_{3}$ für die Richtung der Gewichtskraft des Kreisels, jeweils ausgedrückt im mitrotierenden Hauptachsensystem, auf das sich die Indizes 1,2,3 beziehen. Der Parameter

c={\tfrac {2mgs_{1}}{A}}={\tfrac {2c_{0}}{A}}={\tfrac {c_{0}}{C}}

setzt sich aus der Masse m, der Schwerebeschleunigung g, dem Abstand s₁ des Massenmittelpunkts vom Stützpunkt und dem Hauptträgheitsmoment A um die 1-Achse oder C um die 3-Achse zusammen. Die Konstante c quantifiziert die Wirkung der Gewichtskraft auf den Kreisel und mit c = 0 entsteht ein symmetrischer kräftefreier Euler-Kreisel.

Durch Skalierung der Zeit mit ${\sqrt {c}}$ und der Winkelgeschwindigkeiten mit ${\sqrt {c}}^{\,-1}$ entstehen Bewegungsgleichungen mit c = 1, sodass sie keinen freien Parameter mehr besitzen. Mathematisch reicht es aus, nur diesen einen Fall zu untersuchen[12]. Kowalewskaja skalierte die Längen so, dass A = 2C = 2 wird[13].

Integrale der Bewegung

Abb. 9: Kurven mit k² = 0,36 und n₂ = 0 in Abhängigkeit von c n₁ in der 1-2-Ebene

Wie bei jedem schweren Kreisel ist die Norm des Richtungsvektors der Gewichtskraft, der Drehimpuls in Lotrichtung und die Gesamtenergie E konstant:

{\begin{aligned}{\hat {n}}\cdot {\hat {n}}=&n_{1}^{2}+n_{2}^{2}+n_{3}^{2}=1={\text{const.}}\\l:=&{\frac {{\vec {L}}\cdot {\hat {n}}}{C}}=2pn_{1}+2qn_{2}+rn_{3}={\text{const.}}\\h:=&{\frac {E}{C}}=p^{2}+q^{2}+{\frac {r^{2}}{2}}-{\frac {c}{2}}\,n_{1}={\text{const.}}\end{aligned}}

Diese Konstanten werden in der Kreiseltheorie Integrale genannt, die ersten beiden auch Casimir-Invarianten. Die Gesamtenergie wird in der analytischen Mechanik auch als Hamilton-Funktion bezeichnet, was ihre Benennung mit h begründet. Beim Kowalewskaja-Kreisel gibt es noch ein viertes rationales Integral, die Kowalewskaja-Konstante

K=k^{2}:=(p^{2}-q^{2}+c\,n_{1})^{2}+(2pq+c\,n_{2})^{2}

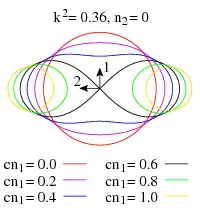
die also nie negativ ist und nur von den Winkelgeschwindigkeiten und Komponenten der Gewichtskraft in der 1-2-Ebene abhängt. Im pqr-Raum der Winkelgeschwindigkeiten um die Hauptachsen definiert diese Konstante momentan also eine zylindrische Fläche mit in r-Richtung konstantem Querschnitt. Wegen K(p,q) = K(-p,-q) ist die Fläche zudem symmetrisch, siehe Abb. 9. Bei negativem c n₁ tauschen p und q die Rollen und es entstehen an einer Diagonalen gespiegelte Figuren. Kowalewskaja benutzte k² als Bezeichnung, es ist aber auch K gebräuchlich[14].

Gleichgewichtslösungen

Relative Gleichgewichte sind Fixpunkte der Kreiselgleichungen, die bei ${\dot {n}}_{1,2,3}={\dot {\omega }}_{1,2,3}={\dot {p}}={\dot {q}}={\dot {r}}=0$ , also bei Konstanz dieser Größen, auftreten[15]:

0 = q r

0 = -r p – c n₃

0 = c n₂

0 = r n₂ – q n₃

0 = p n₃ – r n₁

0 = q n₁ – p n₂

Somit folgt sofort n₂ = 0 und bei q r = 0 sind zwei Fälle zu unterscheiden:

Fall 1, r=0: Aus r = 0 folgt weiter n₃ = n₂ = 0, also n₁ = ±1, und daher schließlich auch q = 0. Dieser Fall entspricht dem lotrecht hängenden oder aufrechten Kreisel, was sich im Bifurkationsdiagramm in Abb. 5 auf den Linien a–b bzw. d–e wieder findet. Erstere Bewegung ist stabil, letztere instabil. Die Kowalewskaja-Konstante lautet hier k² = (p² ± c)², das Drehimpulsquadrat l² = 4p² und je nachdem l² < 4c oder l² > 4c unterscheidet sich der Typ der Instabilität. Die Bereiche werden in Abb. 5 durch den Punkt w getrennt, in dem eine Karussell-Bewegung mit k = 0 stattfindet.

Fall 2, q=0: Im zweiten Fall, q = 0, folgt r p = -c n₃ und aus der vorletzten Euler-Poisson-Gleichung p² + c n₁ = 0. In diesem Fall verschwindet daher die Kowalewskaja-Konstante k und es muss n₁ < 0 sein, sodass der Kreisel ein aufrechter ist mit dem Massenmittelpunkt über dem Stützpunkt. Diese Bewegungen definieren die sogenannten Karussell-Bewegungen des Kreisels und finden sich im Bifurkationsdiagramm in Abb. 5 auf der Strecke u-v-w.

Lagrange- und Hamilton-Funktion des Kowalewskaja-Kreisels

Die theoretische Behandlung des Kowalewskaja-Kreisels geschieht mit der Hamilton-Funktion, die gleich der Gesamtenergie des Kreisels ist. Eine mögliche Formulierung benutzt die lokalen Drehimpulskomponenten L_1,2,3 und den Richtungsvektor der Lotlinie[16]

{\mathcal {H}}({\vec {L}},{\hat {n}})={\frac {E}{C}}={\frac {l_{1}^{2}}{4}}+{\frac {l_{2}^{2}}{4}}+{\frac {l_{3}^{2}}{2}}-cn_{1}

mit

l_{1}={\frac {L_{1}}{C}}=2p,\;l_{2}={\frac {L_{2}}{C}}=2q,\;l_{3}={\frac {L_{3}}{C}}=r

Bei Benutzung der Euler-Winkel ψ, ϑ und φ schreibt sich das

{\mathcal {H}}(\psi ,\vartheta ,\varphi ,p_{\psi },p_{\vartheta },p_{\varphi },)={\frac {E}{C}}={\frac {(p_{\psi }-p_{\varphi }\cos(\vartheta ))^{2}}{4\sin ^{2}(\vartheta )}}+{\frac {p_{\vartheta }^{2}}{4}}+{\frac {p_{\varphi }^{2}}{2}}-c\sin(\vartheta )\sin(\varphi )

siehe Bezugssysteme und Euler-Winkel in der Kreiseltheorie. Darin sind

{\begin{aligned}p_{\psi }=&{\frac {\partial {\mathcal {L}}}{\partial {\dot {\psi }}}}={\dot {\psi }}[1+\sin(\vartheta )^{2}]+{\dot {\varphi }}\cos(\vartheta )={\frac {L_{z}}{C}}={\text{const.}}\\p_{\vartheta }=&{\frac {\partial {\mathcal {L}}}{\partial {\dot {\vartheta }}}}=2{\dot {\vartheta }}\\p_{\varphi }=&{\frac {\partial {\mathcal {L}}}{\partial {\dot {\varphi }}}}={\dot {\psi }}\cos(\vartheta )+{\dot {\varphi }}\end{aligned}}

die konjugierten Impulse zu den Winkeln und

{\mathcal {L}}={\frac {{\dot {\psi }}^{2}}{2}}[1+\sin(\vartheta )^{2}]+{\dot {\psi }}{\dot {\varphi }}\cos(\vartheta )+{\frac {{\dot {\varphi }}^{2}}{2}}+{\dot {\vartheta }}^{2}+c\sin(\vartheta )\sin(\varphi )

die Lagrange-Funktion des Kreisels.

Kowalewskajas Ausarbeitung

Sofia Kowalewskaja[1] gelang die Darstellung aller nötigen Variablen außer dem Präzessionswinkel ψ als hyperelliptische Funktionen der ersten Art, deren beide Argumente linear von der Zeit abhängen. Dazu nutzte sie Variablen s_1,2, die zu einem gewissen Grad die Winkelgeschwindigkeiten p und q ersetzen[17]. Sie ging dabei wie folgt vor.

Die Winkelgeschwindigkeiten p und q sowie die Richtungskomponenten n_1,2 werden mit der imaginären Einheit i jeweils zu einer komplexen Größe zusammen gefasst:

x_{1}:=p+{\text{i}}q,\quad \xi _{1}:=n_{1}+{\text{i}}n_{2}.

Mit den #Euler-Poisson-Gleichungen können die Zeitableitungen

{\begin{aligned}{\dot {x}}_{1}=&{\dot {p}}+{\text{i}}{\dot {q}}=-{\frac {\text{i}}{2}}rx_{1}-{\frac {\text{i}}{2}}c\,n_{3}\\{\dot {\xi }}_{1}=&{\dot {n}}_{1}+{\text{i}}{\dot {n}}_{2}=-{\text{i}}r\xi _{1}+{\text{i}}n_{3}x_{1}\end{aligned}}

gebildet werden, aus denen n₃ elimiert werden kann:

2x_{1}{\dot {x}}_{1}+c{\dot {\xi }}_{1}={\frac {\mathrm {d} }{\mathrm {d} t}}(x_{1}^{2}+c\xi _{1})=-{\text{i}}r(x_{1}^{2}+c\xi _{1})\quad \rightarrow \quad {\frac {\mathrm {d} }{\mathrm {d} t}}\ln(x_{1}^{2}+c\xi _{1})=-{\text{i}}r

Darin steht ln für den natürlichen Logarithmus. Das gleiche Verfahren führt mit den konjugiert komplexen Größen $x_{2}:={\bar {x}}_{1},\xi _{2}:={\bar {\xi }}_{1}$ zu ${\tfrac {\mathrm {d} }{\mathrm {d} t}}\ln(x_{2}^{2}+c\xi _{2})={\text{i}}r$ und die Summe liefert das reelle, nicht negative Integral

{\frac {\mathrm {d} }{\mathrm {d} t}}\ln(x_{1}^{2}+c\xi _{1})+{\frac {\mathrm {d} }{\mathrm {d} t}}\ln(x_{2}^{2}+c\xi _{2})=0\quad \rightarrow \quad k^{2}:=(x_{1}^{2}+c\xi _{1})(x_{2}^{2}+c\xi _{2})={\text{const.}}

Mit den Variablen x_1,2 konnte Kowalewskaja auch r, n₃ sowie ξ_1,2 ausdrücken.

Die Zeitableitungen stellte Kowalewskaja mit neuen Variablen s_1,2 dar, die Nullstellen der Funktion 2. Grades

p(s)=(x_{1}-x_{2})^{2}\left(s-{\frac {1}{2}}l_{1}\right)^{2}-R(x_{1},x_{2})\left(s-{\frac {1}{2}}l_{1}\right)-{\frac {1}{4}}R_{1}(x_{1},x_{2})

in s sind, worin die Koeffizienten

{\begin{aligned}R_{1}(x_{1},x_{2})=&-6l_{1}x_{1}^{2}x_{2}^{2}-(c^{2}-k^{2})(x_{1}+x_{2})^{2}-4lc(x_{1}+x_{2})x_{1}x_{2}+6l_{1}(c^{2}-k^{2})-4l^{2}c^{2}\\R(x_{1},x_{2})=&-x_{1}^{2}x_{2}^{2}+6l_{1}x_{1}x_{2}+2lc(x_{1}+x_{2})+c^{2}-k^{2}\end{aligned}}

Polynome in x_1,2 sind und l₁ = h/3 ist. Für die Nullstellen s_1,2 berechnen sich die Zeitableitungen

{\dot {s}}_{1}={\frac {\sqrt {R_{5}(s_{1})}}{s_{1}-s_{2}}},\quad {\dot {s}}_{2}={\frac {\sqrt {R_{5}(s_{2})}}{s_{2}-s_{1}}}

oder gleichbedeutend[18]

{\begin{aligned}0=&{\frac {\mathrm {d} s_{1}}{\sqrt {R_{5}(s_{1})}}}+{\frac {\mathrm {d} s_{2}}{\sqrt {R_{5}(s_{2})}}}\\\mathrm {d} t=&{\frac {s_{1}\mathrm {d} s_{1}}{\sqrt {R_{5}(s_{1})}}}+{\frac {s_{2}\mathrm {d} s_{2}}{\sqrt {R_{5}(s_{2})}}}\end{aligned}}

Darin ist

R_{5}(s)=-(4s^{3}-g_{2}s-g_{3})\left(s-{\frac {1}{2}}(l_{1}+k)\right)\left(s-{\frac {1}{2}}(l_{1}-k)\right)

ein Polynom 5. Grades in s und

{\begin{aligned}g_{2}=&k^{2}-c^{2}+3l_{1}^{2}\\g_{3}=&l_{1}(k^{2}-c^{2}-l_{1}^{2})+l^{2}c^{2}\end{aligned}}

sind Konstanten der Bewegung. Der erste Faktor im Polynom R₅ hat einen direkten Bezug zur Weierstraß’schen ℘-Funktion. Der Zusammenhang der Differentiale ds_1,2 impliziert, dass sich s_1,2 als Quotienten von Theta-Funktionen, deren Argumente lineare Funktionen der Zeit sind, ausdrücken lassen[19].

Damit ist das Problem im Prinzip gelöst. Kowalewskaja zeigte auf weiteren 50 Seiten, wie alle Variablen mit hyperelliptischen Funktionen dargestellt und mit ihnen beliebige Anfangsbedingungen berücksichtigt werden können. Die Materie ist derart kompliziert, dass es die Wissenschaft noch über ein Jahrhundert beschäftigte, diese Lösungen zu untersuchen und ihre Eigenschaften herauszuarbeiten[20].

Siehe auch

Die anderen beiden, bei beliebigen Anfangsbedingungen immer integrablen Kreiseltypen

der kräftefreie Euler-Kreisel
der schwere symmetrische Lagrange-Kreisel

oder den

Gorjatschew-Tschaplygin-Kreisel, der eine Abwandlung des Kowalewskaja-Kreisels ist.

Fußnoten

Die Artikel
Sophie Kowalevski: Sur le probleme de la rotation d’un corps solide autour d’un point fixe. In: Acta Mathematica. Volume 12, 1889, S. 177–232. (projecteuclid.org [abgerufen am 21. März 2018]).
und
Sophie Kowalevski: Sur une propriété du système d’équations différentielles qui définit la rotation d’un corps solide autour d’un point fixe. In: Acta Mathematica. Volume 14, 1890, S. 81–93 (projecteuclid.org [abgerufen am 21. März 2018]).
enthalten die Ausarbeitungen, die am 25. Dezember 1888 mit dem Bordin-Preis ausgezeichnet wurden.
siehe A. M. Permelov: Kovalevskaya Top: An Elementary Approach. In: Journal of Applied Mathematics and Physics. Vol. 131, Issue 2, 2002, S. 612–620, arxiv:math-ph/0111025v1 (Permelov vereinfacht die Bewegungsfunktionen soweit, dass sie nur wenige Seiten beanspruchen.).
und
Fawzy Mohamed Fahmy El-Sabaa, Alshimaa Abdelbasit Mohamed, Salma Khalel Zakria: The Qualitative and Quantitative Methods of Kovalevskys Case. In: Journal of Applied Mathematics and Physics. Vol. 5, Issue 9, September 2017, ISSN 2327-4379, doi:10.4236/jamp.2017.59155 (scirp.org [abgerufen am 23. März 2018] Studium des Phasen-Portraits, der singulären Punkte und des Bifurkationsdiagramms.).
Tuschmann und Hawig (1993), S. 124.
Magnus (1971), S. 126.
Audin (2008), S. 99.
Richter, Dullin und Wittek (1997), S. 36f.
Richter, Dullin und Wittek (1997), S. 11ff.
Richter, Dullin und Wittek (1997), S. 56f.
Richter, Dullin und Wittek (1997), S. 25f.
Richter, Dullin und Wittek (1997), S. 22f.
Magnus (1971), S. 126, Richter, Dullin und Wittek (1997), S. 12.
Richter, Dullin und Wittek (1997), S. 36.
Kowalewskaja (1888), S. 184.
Richter, Dullin und Wittek (1997), S. 10.
Richter, Dullin und Wittek (1997), S. 11f.
Richter, Dullin und Wittek (1997), S. 36. Dort sind die Bezeichnungen der Winkel ψ und φ jedoch gegenüber der hiesigen vertauscht.
Leimanis (1965), S. 39.
Kowalewskaja benutzte die Bezeichnung R₁(s) statt R₅(s). Für die Wurzeln ist nicht immer das positive Vorzeichen richtig. Wird das Vorzeichen entsprechend angepasst, stimmen die Gleichungen.
Tuschmann und Hawig (1993), S. 129.
siehe beispielsweise Permelov (2002) und Richter, Dullin und Wittek (1997).

Literatur

Wilderich Tuschmann, Peter Hawig: Sofia Kowalewskaja. Ein Leben für Mathematik und Emanzipation. Birkhäuser Verlag, Basel 1993, ISBN 3-0348-5721-7, doi:10.1007/978-3-0348-5720-8 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 25. Mai 2017]).
K. Magnus: Kreisel: Theorie und Anwendungen. Springer, 1971, ISBN 3-642-52163-0, S. 126 ff. (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 20. Februar 2018]).
Peter H. Richter, Holger R. Dullin, Andreas Wittek: Kowalewskaja Kreisel. Institut für den wissenschaftlichen Film (IWF), 1997, abgerufen am 7. April 2018 (Die Dynamik des Kowalewskaja Kreisels wird in einem Film auf mehreren Abstraktionsebenen in erläuterten Animationen und Bildern dargestellt.).
Die schriftliche Ausarbeitung zum Film:
Peter H. Richter, Holger R. Dullin, Andreas Wittek: Kovalevskaya Top. Hrsg.: Institut für den wissenschaftlichen Film (IWF). 1997, ISSN 0073-8433 (englisch, researchgate.net [abgerufen am 28. März 2018]).
Michèle Audin: Remembering Sofya Kovalevskaya. Springer Verlag, London u. a. 2008, ISBN 978-0-85729-928-4, S. 89 ff., doi:10.1007/978-0-85729-929-1 (englisch, eingeschränkte Vorschau in der Google-Buchsuche).
Eugene Leimanis: The General Problem of the Motion of Coupled Rigid Bodies about a Fixed Point. Springer Verlag, Berlin, Heidelberg 1965, ISBN 3-642-88414-8, doi:10.1007/978-3-642-88412-2 (englisch, eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 21. März 2018]).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Kowalewskaja1888-1] Die Artikel
Sophie Kowalevski: Sur le probleme de la rotation d’un corps solide autour d’un point fixe. In: Acta Mathematica. Volume 12, 1889, S. 177–232. (projecteuclid.org [abgerufen am 21. März 2018]).
und
Sophie Kowalevski: Sur une propriété du système d’équations différentielles qui définit la rotation d’un corps solide autour d’un point fixe. In: Acta Mathematica. Volume 14, 1890, S. 81–93 (projecteuclid.org [abgerufen am 21. März 2018]).
enthalten die Ausarbeitungen, die am 25. Dezember 1888 mit dem Bordin-Preis ausgezeichnet wurden.

[2] siehe A. M. Permelov: Kovalevskaya Top: An Elementary Approach. In: Journal of Applied Mathematics and Physics. Vol. 131, Issue 2, 2002, S. 612–620, arxiv:math-ph/0111025v1 (Permelov vereinfacht die Bewegungsfunktionen soweit, dass sie nur wenige Seiten beanspruchen.).
und
Fawzy Mohamed Fahmy El-Sabaa, Alshimaa Abdelbasit Mohamed, Salma Khalel Zakria: The Qualitative and Quantitative Methods of Kovalevskys Case. In: Journal of Applied Mathematics and Physics. Vol. 5, Issue 9, September 2017, ISSN 2327-4379, doi:10.4236/jamp.2017.59155 (scirp.org [abgerufen am 23. März 2018] Studium des Phasen-Portraits, der singulären Punkte und des Bifurkationsdiagramms.).

[3] Tuschmann und Hawig (1993), S. 124.

[4] Magnus (1971), S. 126.

[5] Audin (2008), S. 99.

[6] Richter, Dullin und Wittek (1997), S. 36f.

[7] Richter, Dullin und Wittek (1997), S. 11ff.

[8] Richter, Dullin und Wittek (1997), S. 56f.

[9] Richter, Dullin und Wittek (1997), S. 25f.

[10] Richter, Dullin und Wittek (1997), S. 22f.

[11] Magnus (1971), S. 126, Richter, Dullin und Wittek (1997), S. 12.

[12] Richter, Dullin und Wittek (1997), S. 36.

[13] Kowalewskaja (1888), S. 184.

[14] Richter, Dullin und Wittek (1997), S. 10.

[15] Richter, Dullin und Wittek (1997), S. 11f.

[16] Richter, Dullin und Wittek (1997), S. 36. Dort sind die Bezeichnungen der Winkel ψ und φ jedoch gegenüber der hiesigen vertauscht.

[17] Leimanis (1965), S. 39.

[18] Kowalewskaja benutzte die Bezeichnung R₁(s) statt R₅(s). Für die Wurzeln ist nicht immer das positive Vorzeichen richtig. Wird das Vorzeichen entsprechend angepasst, stimmen die Gleichungen.

[19] Tuschmann und Hawig (1993), S. 129.

[20] siehe beispielsweise Permelov (2002) und Richter, Dullin und Wittek (1997).