Fokaloid

Ein Fokaloid ist eine geometrische Figur, die durch konfokale Ellipsen (2D) oder durch konfokale Ellipsoide (3D) berandet ist.

Fokaloid in 3D

Fokaloid in 2D

Mathematische Definition (3D)

Wird eine Berandung durch ein implizit gegebenes Ellipsoid

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}+{\frac {z^{2}}{c^{2}}}=1$

mit den Halbachsen $a,b,c$ beschrieben, so ist die zweite Berandung durch

${\frac {x^{2}}{a^{2}+\lambda }}+{\frac {y^{2}}{b^{2}+\lambda }}+{\frac {z^{2}}{c^{2}+\lambda }}=1$ gegeben.

Im Grenzfall $\lambda \to 0$ spricht man von dünnen, andernfalls von dicken Fokaloiden.

Konfokalität

Die obigen konfokalen Ellipsoide haben die gleichen Brennpunkte. Mit $a\geq b\geq c$ gilt für deren Abstände $f_{1},\;f_{2},\;f_{3}$ zum Mittelpunkt O:

f_{1}^{2}=a^{2}-b^{2}=(a^{2}+\lambda )-(b^{2}+\lambda )

f_{2}^{2}=a^{2}-c^{2}=(a^{2}+\lambda )-(c^{2}+\lambda )

f_{3}^{2}=b^{2}-c^{2}=(b^{2}+\lambda )-(c^{2}+\lambda )

Definition fokaloide Verteilung

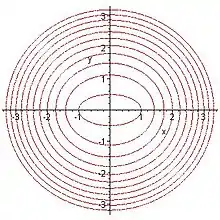
Eine konfokale oder fokaloide Verteilung liegt z. B. vor, wenn die Schichten konstanter Dichte einer Massenverteilung oder die Schichten gleicher Ladungsdichte durch konfokale Ellipsoide bzw. Ellipsen (siehe Bild) gegeben sind.

Linien konstanter Dichte einer konfokalen Verteilung

Physikalische Bedeutung

Fokaloide haben auch Bedeutung in der physikalischen Potentialtheorie. Sie liegt darin, dass zwei konfokale, homogen mit Masse oder Ladung gefüllte Ellipsoide in einem außerhalb befindlichen Probekörper Kräfte bewirken, die in die gleiche Richtung weisen und proportional zu den jeweiligen Massen bzw. Ladungen der jeweils einzelnen Ellipsoide sind.

Hieraus kann man schließen, dass auch verschiedene konfokale, homogen mit Masse oder Ladung gefüllte Fokaloide gleicher Masse bzw. Ladung außerhalb ihrer Ausdehnung unabhängig von ihrer Geometrie die gleiche Wirkung hervorrufen.

Dies bedeutet auch, dass die äußere Wirkung einer fokaloiden Verteilung durch die äußere Wirkung eines dazu konfokalen, homogen mit gleicher Masse gefüllten Ellipsoids beschrieben werden kann.

Weiterhin lässt sich das äußere Feld einer Strecke (dünner Stab) mit homogen darauf verteilter Masse oder konstantem Potential entlang des Stabes als fokaloide Verteilung beschreiben, wobei die Enden der Strecke (des Stabes) die Brennpunkte (Fokusse) des fokaloiden Feldes sind. Die Feldvektoren stehen dabei senkrecht auf den Ellipsoiden gleichen Feldbetrages.

Siehe auch

Literatur

S. Chandrasekhar: Ellipsoidal Figures of Equilibrium. Yale Univ. Press, London 1969.
E. J. Routh: A Treatise on Analytical Statics. Band II. Cambridge University Press, Cambridge 1882.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.