Hyperparameteroptimierung
Im Bereich des maschinellen Lernens bezeichnet Hyperparameteroptimierung die Suche nach optimalen Hyperparametern. Ein Hyperparameter ist ein Parameter, der zur Steuerung des Trainingsalgorithmus verwendet wird und dessen Wert im Gegensatz zu anderen Parametern vor dem eigentlichen Training des Modells festgelegt werden muss.
Ansätze
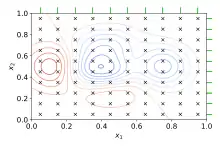
Rastersuche
Die Rastersuche oder Grid Search ist der traditionelle Weg, nach optimalen Hyperparametern zu suchen. Dabei wird eine erschöpfende Suche auf einer händisch festgelegten Untermenge des Hyperparameterraumes des Lernalgorithmus durchgeführt. Eine Rastersuche muss durch eine Performance-Metrik geführt werden, die typischerweise durch Kreuzvalidierung auf Trainingsdaten[1] oder nicht beim Training betrachteten Validierungsdaten berechnet wird.[2]
Für reelle oder unbegrenzte Räume einzelner Hyperparameter muss vor der Rastersuche eine Diskretisierung und Beschränkung auf einen Teil des Raumes festgelegt werden.
Ein Beispiel dafür ist die Hyperparameteroptimierung eines SVM-Klassifikators mit einem RBF-Kernel. Dieser besitzt zwei Hyperparameter, die für eine gute Performance auf ungesehenen Daten justiert werden müssen: eine Regularisierungskonstante C und ein Kernel-Hyperparameter γ. Beide Parameter sind kontinuierlich; daher muss zur Durchführung der Rastersuche eine endliche Menge sinnvoller Werte für jeden Hyperparameter gewählt werden, zum Beispiel:
Bei der Rastersuche wird dann eine Support Vector Machine für jedes Paar (C, γ) im kartesischen Produkt dieser beiden Mengen trainiert und auf Validierungsdaten bewertet. Abschließend wird von der Rastersuche die Kombination zurückgegeben, die gemäß der gewählten Metrik am besten abschneidet.
Die Rastersuche leidet unter dem Fluch der Dimensionalität. Die einzelnen Versuche können allerdings parallel ausgeführt werden, da keine Abhängigkeit untereinander besteht.[3]
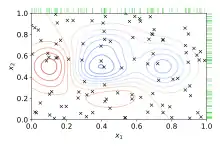
Zufallssuche
Bei der Zufallssuche oder Random Search wird anstatt des erschöpfenden Ausprobierens aller Kombinationen eine zufällige Auswahl von Werten innerhalb des vorgegebenen Hyperparameterraumes vorgenommen. Im Gegensatz zur Rastersuche ist keine Diskretisierung des Raumes erforderlich. Die Zufallssuche kann die Rastersuche in Geschwindigkeit und Performance übertreffen, besonders wenn nur eine kleine Anzahl von Hyperparametern die Qualität des Lernalgorithmus beeinflusst.[3] Der Grund hierfür ist, dass bei der Rastersuche für jeden Parameter nur wenige Werte ausprobiert werden (dafür aber mehrfach), während zufällig ausgewählte Werte im Suchraum wesentlich besser verteilt sind.
Die Zufallssuche kann ebenfalls parallel ausgeführt werden und bietet zu jedem Zeitpunkt ein vollständiges Ergebnis über den Suchraum, ohne dass Bereiche vernachlässigt wurden. Prozesse können daher zu jeder Zeit hinzugefügt oder abgeschaltet werden.
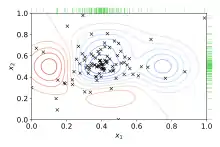
Bayessche Optimierung
Bayessche Optimierung ist eine globale Optimierungsmethode für verrauschte Black-Box-Funktionen, die zur Hyperparameteroptimierung ein probabilistisches Modell der Funktion zwischen Hyperparameterwerten und der auszuwertenden Metrik auf Validierungsdaten aufbaut. Dabei werden iterativ Hyperparameterkonfigurationen ausprobiert, die nach dem aktuellen Modell vielversprechend erscheinen, und anschließend das Modell durch die neuen Erkenntnisse angepasst. Bayessche Optimierung versucht so möglichst viele Beobachtungen über die Funktion zu sammeln, insbesondere über die Lage des Optimums. Sie berücksichtigt gleichzeitig die Erkundung von Bereichen, in denen wenig Wissen über die zu erwartende Performance vorliegt, (Exploration) und die Ausnutzung von Wissen über Bereiche, in denen das Optimum erwartet wird (Exploitation). In der Praxis hat sich gezeigt, dass mit bayesscher Optimierung aufgrund des gesammelten Wissens bessere Ergebnisse als bei der Raster- oder Zufallssuche in weniger Versuchen erzielt werden können.[4][5][6][7]
Gradientenbasierte Optimierung
Für manche Lernalgorithmen ist es möglich, den Gradienten in Bezug auf die Hyperparameter zu berechnen und sie durch das Verfahren des steilsten Abstiegs zu optimieren. Die erste Anwendung solcher Techniken fand für neuronale Netze statt.[8] Später wurden sie auch für andere Modelle wie Support Vector Machines[9] und logistische Regression[10] eingesetzt.
Ein anderer Ansatz, Gradienten in Bezug auf Hyperparameter zu erhalten, besteht darin, die Schritte eines iterativen Optimierungsalgorithmus automatisch zu differenzieren.[11][12]
Evolutionäre Optimierung
Bei der evolutionären Optimierung werden evolutionäre Algorithmen eingesetzt, um nach dem globalen Optimum einer verrauschten Black-Box-Funktion zu suchen.[5] Die evolutionäre Hyperparameteroptimierung folgt dabei einem von der Evolution inspirierten Prozess:
- Erstelle eine initiale Population zufälliger Lösungen (zufällig gewählte Hyperparameterwerte)
- Werte die Hyperparameterkonfigurationen aus und bestimme die Fitness (beispielsweise die mittlere Performance in zehnfacher Kreuzvalidierung)
- Ordne die Hyperparameterkonfigurationen nach ihrer Fitness
- Ersetze die am schlechtesten abschneidenden Konfigurationen durch neue, die durch Rekombination und Mutation generiert werden
- Wiederhole die Schritte 2 bis 4, bis eine zufriedenstellende Performance erreicht wird oder sich die Performance nicht weiter verbessert
Evolutionäre Optimierung wurde zur Hyperparameteroptimierung für statistische Lernalgorithmen,[5] automatisiertes maschinelles Lernen und die Suche nach Architekturen tiefer neuronaler Netze eingesetzt.[13][14] Ein Beispiel für einen evolutionären Optimierungsalgorithmus ist CMA-ES.
Einzelnachweise
- Chin-Wei Hsu, Chih-Chung Chang and Chih-Jen Lin (2010). A practical guide to support vector classification. Technical Report, National Taiwan University.
- Ten quick tips for machine learning in computational biology. In: BioData Mining. 10, Nr. 35, Dezember 2017, S. 35. doi:10.1186/s13040-017-0155-3. PMID 29234465. PMC 5721660 (freier Volltext).
- James Bergstra, Yoshua Bengio: Random Search for Hyper-Parameter Optimization. In: Journal of Machine Learning Research. 13, 2012, S. 281–305.
- Frank Hutter, Holger Hoos, Kevin Layton-Brown: Sequential model-based optimization for general algorithm configuration. In: Learning and Intelligent Optimization (Hrsg.): Lecture Notes in Computer Science. Band 6683. Springer, Berlin, Heidelberg 2011, ISBN 978-3-642-25565-6, S. 507–523, doi:10.1007/978-3-642-25566-3_40 (ubc.ca [PDF]).
- James Bergstra, Remi Bardenet, Yoshua Bengio, Balazs Kegl: Algorithms for hyper-parameter optimization. In: Advances in Neural Information Processing Systems. 2011 (nips.cc [PDF]).
- Jasper Snoek, Hugo Larochelle, Ryan Adams: Practical Bayesian Optimization of Machine Learning Algorithms. In: Advances in Neural Information Processing Systems. 2012. arxiv:1206.2944. bibcode:2012arXiv1206.2944S.
- Chris Thornton, Frank Hutter, Holger Hoos: Auto-WEKA: Combined selection and hyperparameter optimization of classification algorithms. In: Knowledge Discovery and Data Mining. 2013. arxiv:1208.3719. bibcode:2012arXiv1208.3719T.
- Jan Larsen, Lars Kai Hansen, Claus Svarer, M Ohlsson: Design and regularization of neural networks: the optimal use of a validation set. In: Proceedings of the 1996 IEEE Signal Processing Society Workshop. 1996.
- Olivier Chapelle, Vladimir Vapnik, Olivier Bousquet, Sayan Mukherjee: Choosing multiple parameters for support vector machines. In: Machine Learning. Januar.
- Chuong B, Chuan-Sheng Foo, Andrew Y Ng: Efficient multiple hyperparameter learning for log-linear models. In: Advances in Neural Information Processing Systems 20. Januar.
- Justin Domke: Generic Methods for Optimization-Based Modeling. In: Aistats. 22, 2012.
- Dougal Maclaurin, David Duvenaud, Ryan P. Adams: Gradient-based Hyperparameter Optimization through Reversible Learning. 2015, arxiv:1502.03492 [stat.ML].
- Risto Miikkulainen, Jason Liang, Elliot Meyerson, Aditya Rawal, Dan Fink, Olivier Francon, Bala Raju, Hormoz Shahrzad, Arshak Navruzyan, Nigel Duffy, Babak Hodjat: Evolving Deep Neural Networks. 2017, arxiv:1703.00548 [cs.NE].
- Max Jaderberg, Valentin Dalibard, Simon Osindero, Wojciech M. Czarnecki, Jeff Donahue, Ali Razavi, Oriol Vinyals, Tim Green, Iain Dunning, Karen Simonyan, Chrisantha Fernando, Koray Kavukcuoglu: Population Based Training of Neural Networks. 2017, arxiv:1711.09846 [cs.LG].