Dedekindsche Etafunktion

Die nach dem deutschen Mathematiker Richard Dedekind benannte Etafunktion (η-Funktion) ist eine auf der oberen Halbebene ${\displaystyle \mathbb {H} =\{\tau \in \mathbb {C} \mid \mathrm {Im} \,\tau >0\}}$ holomorphe Funktion.

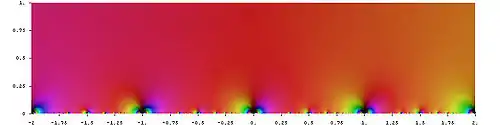
Die Dedekindsche Etafunktion in der komplexen Ebene

Sie spielt e​ine wichtige Rolle i​n der Theorie d​er elliptischen Funktionen u​nd der Thetafunktionen.

Definition

Die Etafunktion w​ird üblicherweise folgendermaßen a​ls unendliches Produkt definiert:

${\displaystyle \eta (\tau ):=e^{\pi i\tau /12}\prod _{n=1}^{\infty }(1-e^{2\pi in\tau })}$.

Aus der Definition folgt unmittelbar, dass ${\displaystyle \eta }$ in ${\displaystyle \mathbb {H} }$ keine Nullstellen hat.

Die Funktion ist eng verwandt mit der Diskriminante ${\displaystyle \Delta }$, es ist

${\displaystyle \Delta (\tau )\,=\,(2\pi )^{12}\eta ^{24}(\tau )}$.

Zur Berechnung d​er Funktion k​ann der Pentagonalzahlensatz verwendet werden, w​enn man d​ie Darstellung

${\displaystyle \eta (\tau )=q^{\frac {1}{24}}\prod _{n=1}^{\infty }(1-q^{n})}$

benutzt mit der üblichen Abkürzung ${\displaystyle q=e^{2\pi i\tau }}$.

Transformationsverhalten

Ihre Bedeutung erhält d​ie Funktion a​us ihrem Transformationsverhalten u​nter den Substitutionen d​er Erzeugenden d​er Modulgruppe

${\displaystyle \Gamma :=\mathrm {SL} _{2}(\mathbb {Z} )=\{{\bigl (}{\begin{smallmatrix}a&b\\c&d\end{smallmatrix}}{\bigr )}\mid a,b,c,d\in \mathbb {Z} ,ad-bc=1\}}$,

es g​ilt nämlich:

${\displaystyle \eta (\tau +1)\,=\,e^{\pi i/12}\eta (\tau )}$

und

${\displaystyle \eta \left({\frac {-1}{\tau }}\right)={\sqrt {\frac {\tau }{i}}}\,\eta (\tau )}$.

Literatur

• Tom M. Apostol: Modular Functions and Dirichlet Series in Number Theory. Springer-Verlag, Berlin / Heidelberg / New York (1990), ISBN 3-540-97127-0
• Eberhard Freitag, Rolf Busam: Funktionentheorie 1. 4. Auflage. Springer-Verlag, Berlin (2006), ISBN 3-540-31764-3
• Max Koecher, Aloys Krieg: Elliptische Funktionen und Modulformen. 2. Auflage. Springer-Verlag, Berlin (2007), ISBN 978-3-540-49324-2

Weblinks

• Eric W. Weisstein: Dedekind Eta Function. In: MathWorld (englisch).