Unsymmetrischer Kreisel
Der unsymmetrische oder asymmetrische Kreisel ist in der Kreiseltheorie ein Kreisel mit drei verschiedenen Hauptträgheitsmomenten[1].
Für den allgemeinen Fall des unsymmetrischen schweren Kreisels ist Anfang des 21. Jahrhunderts noch keine Lösung der Eulerʹschen Kreiselgleichungen gefunden worden. Da nur wenige Lösungen und auch nur für spezielle Fälle vorliegen, fehlt die analytische Beschreibung für die große Mehrheit der Kreisel. Die aktuelle Forschung beschäftigt sich unter anderem mit der Herausarbeitung invarianter Eigenschaften des dynamischen Systems.[2]
Bezeichnungen
Ein Symmetrischer Kreisel wird abgeplattet genannt, wenn sein axiales Drehmoment größer ist als seine äquatorialen, und im umgekehrten Fall wird er gestreckt genannt. Beim unsymmetrischen Kreisel werden ähnliche Bezeichnungen verwendet[1]. Sind A, B und C die Hauptträgheitsmomente um die erste, zweite bzw. dritte Hauptträgheitsachse und gilt A > B > C, dann ist der Kreisel
- bezüglich der 1-Achse kurzachsig (entsprechend einem abgeplatteten symmetrischen Kreisel),
- bezüglich der 2-Achse mittelachsig und
- bezüglich der 3-Achse langachsig (entsprechend einem gestreckten symmetrischen Kreisel).
Hauptträgheitsmomente
Der unsymmetrische Kreisel hat drei verschiedene Hauptträgheitsmomente A, B und C. Bei einem Starrkörper erfüllen sie die Dreiecksungleichungen
- A + B > C, B + C > A und A + C > B
siehe Trägheitsmoment. Dann kann es einen unsymmetrischen Kreisel mit den Hauptträgheitsmomenten A, B und C geben.
Eines dieser Trägheitsmomente kann dazu benutzt werden, die Energie oder die Zeit so zu skalieren, dass in den betrachteten physikalischen Gesetzen, insbesondere den Eulerʹschen Kreiselgleichungen, das betreffende Trägheitsmoment gleich eins wird[3]. Daher besitzen zwei Kreisel, bei denen das Verhältnis zweier ihrer Hauptträgheitsmomente zum dritten gleich ist, vergleichbare Drehträgheitseigenschaften. Das gestattet die möglichen Parameterkombinationen {A, B, C} um eine Dimension auf {α, β}={B/A, C/A} zu reduzieren. Für diese dimensionslosen Parameter gelten die Einschränkungen
- α + 1 > β, α + β > 1 und 1 + β > α.
Darstellung der Kreiseltypen
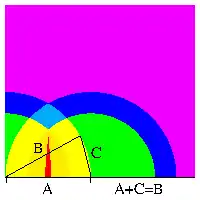a) Darstellung als Dreieck
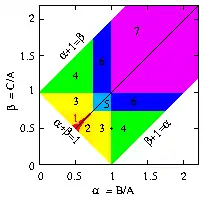b) Darstellung als Punkt in der α-β-Ebene
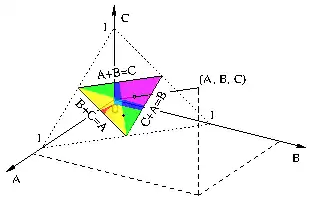c) Darstellung als Punkt im Formdreieck
Die Bilder zeigen Darstellungsmöglichkeiten für Kreiseltypen[4]. Der Parameterraum ist nach den sieben von Katok und Richter gefundenen Bereichen eingefärbt, in denen die Energiefläche des Kreisels vergleichbare topologische Eigenschaften besitzt[5]. Der Kowalewskaja-Kreisel, bei dem α = 1 und β = 1/2 ist, ist als Dreieck (a) oder als Punkt (b,c) eingetragen. Die Kreiseltypen sind in den Bildern wie folgt veranschaulicht:
- a) Als Dreieck
- Weil die Hauptträgheitsmomente die Dreiecksungleichungen erfüllen, kann ein Kreisel mit Haupträgheitsmomenten A, B und C durch ein Dreieck mit entsprechenden Seitenlängen repräsentiert werden. Bei festgehaltener Seite A liegt die gegenüber liegende Ecke in der oberen Halbebene. Ein unsymmetrischer Kreisel entspricht dann einem unregelmäßigen Dreieck und der eingezeichnete symmetrische Kowalewskaja-Kreisel einem gleichschenkligen Dreieck. Ein Kugelkreisel mit drei gleichen Hauptträgheitsmomenten entspricht einem gleichseitigen Dreieck.
- b) Als Punkt in der α-β-Ebene
- Ein Kreisel mit den dimensionslosen Verhältnissen α = B/A und β = C/A entspricht einem Punkt in der α-β-Ebene. Der Streifen zwischen α + 1 = β und β + 1 = α dehnt sich nach oben rechts bis ins Unendliche aus. Die symmetrischen Kreisel liegen auf den Geraden α = β, α = 1 oder β = 1 und der Kugelkreisel liegt im Punkt (1, 1).
- c) Als Punkt im Formdreieck
- Das Formdreieck hat im Raum, in dem die Hauptträgheitsmomente auf den Koordinatenachsen aufgetragen werden, die Ecken in den Punkten (½, ½, 0), (½, 0, ½) und (0, ½, ½) und ist im Bild farbig dargestellt. In diesem Koordinatensystem entspricht ein gegebener Kreisel einem Punkt P = (A, B, C) und zu ihm verwandte Kreisel mit ähnlichen Drehträgheitseigenschaften liegen auf der Geraden durch den Ursprung 0 und P. Der Durchstoßpunkt dieser Geraden durch die Ebene A + B + C = 1 liegt im sogenannten Formdreick. Es ist die einzige der gezeigten Repräsentationen, die alle Kreisel umfasst und trotzdem nur eine endliche Ausdehnung besitzt. Die symmetrischen Kreisel liegen auf einer Seitenhalbierenden und der Kugelkreisel liegt im Schwerpunkt (1/3, 1/3, 1/3).
Pseudoreguläre Präzession
Der allgemeine unsymmetrische Kreisel kann nur die Staude-Drehung gleichmäßig ausführen. Eine pseudo-reguläre Präzession, d. h. eine mit dem Auge von einer regulären Präzession nicht unterscheidbare Bewegung, kann der unsymmetrische Kreisel dann ausführen, wenn er sich rasch um eine Hauptträgheitsachse dreht, deren Hauptträgheitsmoment A das größte oder das kleinste Hauptträgheitsmoment ist. Die sich ergebende Präzession gleicht im Mittel der pseudoregulären Präzession eines Lagrange-Kreisels mit gleichem axialen Trägheitsmoment A und gleichem Stützpunktsmoment, siehe Hauptartikel. Begleitet wird diese Präzession von vier Nutationen in Form von Epizykeln, die bis ins 17. Jahrhundert hinein für die Erklärung der Planetenbahnen benutzt wurden.
Siehe auch
- Schwerer Kreisel: Kreisel im Schwerefeld der Erde.
- Symmetrischer Kreisel: Kreisel mit zwei gleichen Hauptträgheitsmomenten.
- Dschanibekow-Effekt: Spezielle Bewegung eines kräftefreien unsymmetrischen Kreisels.
Bewegungsformen unsymmetrischer schwerer Kreisel:
Weblinks
Einzelnachweise
- Magnus (1971), S. 20.
- Gashenenko und Richter (2004), S. 2527.
- Gashenenko und Richter (2004), S. 2526.
- Magnus (1971), S. 21 f.
- Gashenenko und Richter (2004), S. 2542.
Literatur
- K. Magnus: Kreisel: Theorie und Anwendungen. Springer, 1971, ISBN 978-3-642-52163-8, S. 20 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 20. Februar 2018]).
- R. Grammel: Der Kreisel. Seine Theorie und seine Anwendungen. Vieweg Verlag, Braunschweig 1920, DNB 451641280, S. 39 (archive.org – "Schwung" bedeutet Drehimpuls, "Drehstoß" Drehmoment und "Drehwucht" Rotationsenergie).
oder
R. Grammel: Der Kreisel. Theorie des Kreisels. 2. überarb. Auflage. Band 1.. Springer, Berlin, Göttingen, Heidelberg 1950, DNB 451641299, S. 121 ff. - F. Klein, A. Sommerfeld: Theorie des Kreisels. Die technischen Anwendungen der Kreiseltheorie. Heft IV. Teubner, Leipzig 1910, S. 767 (archive.org [abgerufen am 21. Oktober 2017]).
- I. G. Gashenenko, P. H. Richter: Enveloping Surfaces And Admissible Velocities Of Heavy Rigid Bodies. In: World Scientific Publishing Company (Hrsg.): International Journal of Bifurcation and Chaos. Band 14, Nr. 8, 2004, ISSN 0218-1274, S. 2525–2553, doi:10.1142/S021812740401103X (iamm.su [PDF; abgerufen am 2. Juni 2019]).