Richtungskosinus

In der Vektorrechnung sind die Richtungskosinus eines Vektors des euklidischen Raums ${\displaystyle \mathbb {R} ^{3}}$ die Kosinuswerte seiner Richtungswinkel, also der Winkel zwischen dem Vektor und den drei Standardbasisvektoren ${\displaystyle {\vec {e}}_{1}}$, ${\displaystyle {\vec {e}}_{2}}$, ${\displaystyle {\vec {e}}_{3}}$.[1][2]

Vektor ${\displaystyle {\vec {v}}}$ mit den Richtungswinkeln ${\displaystyle \alpha _{1}}$, ${\displaystyle \alpha _{2}}$, ${\displaystyle \alpha _{3}}$.

Eigenschaften

Für den Vektor ${\displaystyle {\vec {v}}={\begin{pmatrix}v_{1}\\v_{2}\\v_{3}\end{pmatrix}}}$ sind die Richtungskosinus

${\displaystyle \cos \alpha _{1}={\frac {{\vec {v}}\cdot {\vec {e}}_{1}}{|{\vec {v}}|\,|{\vec {e}}_{1}|}}={\frac {v_{1}}{|{\vec {v}}|}}={\frac {v_{1}}{\sqrt {v_{1}^{2}+v_{2}^{2}+v_{3}^{2}}}}}$,

${\displaystyle \cos \alpha _{2}={\frac {{\vec {v}}\cdot {\vec {e}}_{2}}{|{\vec {v}}|\,|{\vec {e}}_{2}|}}={\frac {v_{2}}{|{\vec {v}}|}}={\frac {v_{2}}{\sqrt {v_{1}^{2}+v_{2}^{2}+v_{3}^{2}}}}}$,

${\displaystyle \cos \alpha _{3}={\frac {{\vec {v}}\cdot {\vec {e}}_{3}}{|{\vec {v}}|\,|{\vec {e}}_{3}|}}={\frac {v_{3}}{|{\vec {v}}|}}={\frac {v_{3}}{\sqrt {v_{1}^{2}+v_{2}^{2}+v_{3}^{2}}}}}$,

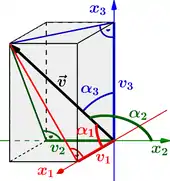
wie auch aus den farbigen Dreiecken in der nebenstehenden Abbildung abgelesen werden kann. Umgekehrt kann ${\displaystyle {\vec {v}}}$ durch seinen Betrag und die Richtungskosinus ausgedrückt werden,

${\displaystyle {\vec {v}}=|{\vec {v}}|{\begin{pmatrix}\cos \alpha _{1}\\\cos \alpha _{2}\\\cos \alpha _{3}\end{pmatrix}}}$.

Wenn dies durch ${\displaystyle |{\vec {v}}|}$ dividiert wird, zeigt sich, dass die Richtungskosinus gerade die Komponenten des Einheitsvektors ${\displaystyle {\vec {e}}_{v}}$ in Richtung von ${\displaystyle {\vec {v}}}$ sind,

${\displaystyle {\vec {e}}_{v}={\frac {\vec {v}}{|{\vec {v}}|}}={\begin{pmatrix}\cos \alpha _{1}\\\cos \alpha _{2}\\\cos \alpha _{3}\end{pmatrix}}}$.

Wegen ${\displaystyle |{\vec {e}}_{v}|=1}$ ist

${\displaystyle \cos ^{2}\alpha _{1}+\cos ^{2}\alpha _{2}+\cos ^{2}\alpha _{3}=1}$.

Da die Richtungswinkel auf den Bereich zwischen ${\displaystyle 0}$ und ${\displaystyle \pi }$ beschränkt sind und der Kosinus in diesem Intervall umkehrbar ist, sind mit den Richtungskosinus auch die drei Richtungswinkel gegeben.

Einzelnachweise

1. Gert Böhme: Einführung in die höhere Mathematik (= Mathematik – Vorlesungen für Ingenieurschulen. Band 2). Springer, 1964, S. 103–105 (eingeschränkte Vorschau in der Google-Buchsuche).
2. Eric W. Weisstein: Direction Cosine. In: MathWorld (englisch).