Fusion mittels magnetischen Einschlusses
Fusion mittels magnetischen Einschlusses ist der heute meistverfolgte Entwicklungsweg zur angestrebten technischen Gewinnung von elektrischer Energie aus der Kernfusion. Konzepte, kommerziell verwertbare elektrische Leistung mit einem auf magnetischem Einschluss beruhenden Reaktor zu erzeugen, bezeichnet man auch als Magnetische Fusionsenergie, kurz MFE. Allgemein wird der Weg zur Fusionsenergiegewinnung durch magnetischen Einschluss als weiter fortgeschritten und vielversprechender erachtet als die ebenfalls untersuchte Trägheitsfusion.
.png.webp)
Bei den heute konkret verfolgten Projekten der Fusion von leichteren Atomkernen zu schwereren werden die Wasserstoff-Isotope Deuterium und Tritium verwendet, die sich dabei in Helium-4 verwandeln (siehe auch Kernfusionsreaktor). Eine einzelne Fusionsreaktion erfolgt, wenn sich ein Deuterium- und ein Tritiumkern sehr nahe kommen. Das ist wegen der gegenseitigen elektrostatischen Abstoßung der positiv geladenen Kerne nur mit sehr hoher kinetischer Energie der Reaktionspartner im Bereich von 10 bis 20 keV erreichbar, was Temperaturen von etwa 100–250 Millionen Grad Celsius entspricht. Bei diesen Temperaturen sind Atomkerne und Elektronen getrennt voneinander und bilden ein Plasma.
Ein solches Plasma lässt sich nicht in materielle Gefäße einschließen, da es bei Berührung mit den kalten Wänden sofort so stark abkühlen würde, dass der Plasmazustand beendet wird. Eine Möglichkeit, ein so heißes Plasma einzuschließen, sind geeignet geformte Magnetfelder. Ihre Einwirkung (Lorentzkraft) auf die sich bewegenden, geladenen Plasmateilchen kann diese von der Gefäßwand fernhalten. Betrachtet man das Plasma in seinem magnetischen Gefäß als ein Fluid, dann wird sein nach außen gerichteter Druck durch den nach innen gerichteten Magnetfelddruck (eine formale Rechengröße, nicht anschaulich wie mechanischer Druck aufzufassen) kompensiert. Der notwendige Plasmadruck der Größenordnung 1 bar konnte in den bisherigen Experimenten sekunden- bis minutenlang aufrechterhalten werden.
Aus der Vielfalt möglicher Magnetfeldanordnungen haben sich zwei Konzepte mit toroidaler Geometrie als am meisten erfolgversprechend herauskristallisiert: der Tokamak und der Stellarator. Die größten dieser Experimente sind
- der Tokamak JET (in Betrieb seit 1983), mit dem kurzzeitig bereits Fusionsleistung im Megawatt-Maßstab erzeugt wurde,
- das Heliotron LHD (seit 1998 in Betrieb),
- der Stellarator Wendelstein 7-X (in Betrieb seit 2015[2]), der ein stabiles Plasma mit fusionsrelevanten Parametern für 30 Minuten aufrechterhalten soll,
- der Tokamak ITER (Bau begonnen 2006, geplante Fertigstellung 2025), mit dem erstmals Fusionsleistung „netto“ (also den Heizleistungsbedarf übersteigend) erzeugt werden soll.
Alle bisherigen Forschungsbemühungen sind darauf gerichtet, im genannten Temperaturbereich längere Zeit stabile Plasmen zu erzeugen. Dafür wurde – außer in einigen wenigen Versuchen in den Anlagen TFTR (Tokamak Fusion Test Reactor, USA) und JET – noch kein Deuterium-Tritium-Gemisch, sondern gewöhnlicher Wasserstoff oder in einigen Fällen reines Deuterium verwendet.
Plasmaeinschluss durch Magnetfelder
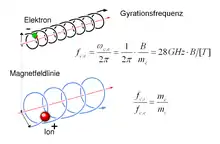
Fusion mit magnetischem Einschluss beruht auf der Lorentzkraft. Diese hält die geladenen Plasmateilchen, Elektronen und Ionen, im Magnetfeld auf schraubenförmigen Bahnen. Eine solche Teilchenbahn kann man sich als Kombination einer Bewegung entlang einer Magnetfeldlinie und – senkrecht dazu – einer kreisförmigen Bewegung um die Feldlinie herum (Gyration) vorstellen.
Der einfachste magnetische Einschluss lässt sich mit einer langen Zylinderspule erreichen. Das Magnetfeld einer solchen Spule ist parallel zur Spulenachse gerichtet; es verhindert den Verlust der Teilchen in radialer Richtung, aber nicht entlang der Achse, also an den Spulenenden. Um diese Endverluste zu vermeiden, gibt es im Wesentlichen zwei Methoden. Bei der einen versucht man magnetische Spiegel an den Spulenenden aufzubauen, bei der anderen biegt man gewissermaßen die Zylinderspule zu einem geschlossenen Ring (Torus) zusammen.
Magnetische Spiegel
Ein aktives Forschungsgebiet in den Anfangsjahren der Fusionsforschung waren magnetische Spiegelanordnungen (Fachjargon: „Spiegelmaschinen“), da diese gegenüber torusförmigen Anordnungen große Vorteile in praktisch-technischer Hinsicht, z. B. hinsichtlich Wartungsarbeiten und Auswechseln von Teilen, haben. Die meisten der konstruierten Spiegelmaschinen versuchten das Plasma an den Enden der Spule durch nichtplanare magnetische Felder einzuschließen. Zwar genügt der einfache Spiegel mit seinem flaschenhalsförmigen Verlauf der Feldlinien nicht zum Festhalten des heißen Fusionsplasmas, aber mit zusätzlichen Magneten von mehr oder weniger komplizierter Form lässt sich erreichen, dass die Feldlinien größtenteils im Inneren des Einschlussvolumens in sich zurückgebogen werden, so dass auch schnelle Teilchen eingeschlossen bleiben. Aus Symmetriegründen gibt es jedoch in jeder Spiegelkonfiguration eine für die Teilchen durchlässige Stelle. Anschaulich bedeutet dies, es gibt eine Feldlinie, die nicht im Inneren des Gefäßes geschlossen ist, sondern aus dem Einschlussgebiet hinaus führt. Auch fortschrittliche Konstruktionen (wie z. B. beim MFTF-Experiment) können dies niemals völlig unterbinden.
Toroidale Anordnungen
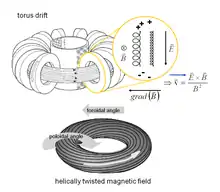
Ein ausschließlich toroidales Magnetfeld kann wegen der Gradienten- und Krümmungsdrift geladene Teilchen nicht einschließen (s. Abbildung): Bei einer toroidalen Anordnung von Spulen ist notwendigerweise auf der Innenseite, wo die Spulen dichter stehen, die Magnetfeldstärke höher als auf der Außenseite. Die Elektronen und Ionen führen daher keine exakt kreisförmigen Schraubenbewegungen um die Feldlinien aus, sondern die Krümmung ihrer Schraubenbahnen ist zur Torus-Innenseite jeweils etwas enger als außen. Die Teilchenbahnen von Elektronen und Ionen driften daher wie in der Abbildung gezeigt nach oben bzw. unten. Wegen der daraus resultierenden Ladungstrennung entsteht ein elektrisches Vertikalfeld. Dieses elektrische Feld führt zusammen mit dem Magnetfeld zu einer weiteren Drift, welche die Teilchen nach außen bringt und somit den Einschluss zerstört.
Ausweg ist, neben der toroidalen eine poloidale Komponente des Magnetfeldes zu verwenden, so dass sich die Magnetfeldlinien schraubenförmig (helikal) um den Torus herumwinden. Die ihrer Feldlinie folgenden Plasmateilchen erfahren damit abwechselnd eine Drift zum Plasmazentrum und von diesem weg, so dass insgesamt keine Ladungstrennung stattfindet.
Wie die poloidale Magnetfeldkomponente erzeugt wird, unterscheidet Tokamak und Stellarator: Beim Tokamak bewirkt dies ein induzierter, im Plasma fließender Strom (mit Nachteilen für die Plasmastabilität), beim Stellarator besonders aufwändig geformte Magnetspulen.
Ein früher Versuch, ein System für magnetischen Einschluss zu bauen, war der 1951 von Lyman Spitzer entwickelte Stellarator (von lat. stella „Stern“, als Anspielung auf die Energieerzeugung durch Kernfusion in Gestirnen). Dieser bestand im Wesentlichen aus einem in zwei Halbringe geteilten Torus, dessen Hälften über zwei gerade, sich kreuzende Rohre zu einer Acht verbunden waren. Dies hat zum Ergebnis, dass Teilchen, die während des Umlaufs durch die halbe Acht von innen nach außen gewandert sind, sich beim Eintritt in die andere Hälfte der Acht wieder innen befinden. Bei neueren Stellarator-Konzepten wird das Ausmitteln dieser Drift dadurch erreicht, dass das Magnetfeld das Plasma ständig auch um die dem Mittekreis folgende eigene Achse umlaufen lässt.
1968 wurden erstmals die russischen Forschungsergebnisse über den Tokamak veröffentlicht, mit Ergebnissen, die alle bis dahin konkurrierenden Fusionsreaktorkonzepte, ob magnetisch oder nicht, bei weitem in den Schatten stellten. Seit dieser Zeit ist das Tokamak-Prinzip das meistverfolgte Konzept für magnetischen Einschluss. In einem Tokamak wird ein poloidales Feld durch einen im Plasma fließenden Strom erzeugt. Dieses poloidale Feld führt, zusammen mit dem von Spulen erzeugten toroidalen Feld, zur Verdrillung der Feldlinien. Im Gegensatz zum Stellarator, wo das Magnetfeld eine dreidimensionale Struktur besitzt, ist es im Tokamak zweidimensional, d. h. es ist rotationssymmetrisch um die Torusachse.
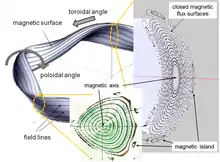
Im toroidalen Einschluss bilden die helikal verdrillten magnetischen Feldlinien zwiebelartig ineinandergeschachtelte magnetische Flussflächen um die zentrale magnetische Achse. Da sich die Feldlinien nicht schneiden können, lässt sich jeder Flussfläche eine feste Verdrillung (Rotationstransformation) zuordnen. Ohne weitere Störungen würde sich ein geladenes Teilchen immer auf derselben Flussfläche bewegen, auf der es toroidal und poloidal umläuft. Damit bildet sich auf einer Flussfläche durch Stöße ein Gleichgewicht zwischen den Plasmateilchen aus, d. h., es können ihnen auf der Flussfläche thermodynamische Größen zugeordnet werden, z. B. eine gemeinsame Temperatur und Dichte und damit ein gemeinsamer Druck. Die Abbildung zeigt im linken Teil eine solche Flussfläche mit einigen markierten Feldlinien. Im gezeigten Fall eines Stellarators hat diese Flussfläche eine dreidimensional geformte Struktur; im Fall eines Tokamaks wäre sie kontinuierlich rotationssymmetrisch um die Achse des Torus. Rechts und unten sind Querschnitte (Poincaré-Plots) gezeigt, die die Durchstoßpunkte von Feldlinien durch einen poloidalen Querschnitt darstellen. Man erkennt die ineinandergeschachtelte Struktur der geschlossenen Flussflächen im Einschlussgebiet. Rechts im Bild ist der berechnete Poincaré-Plot für eine poloidale Ebene mit bananenförmigem Querschnitt in einer magnetischen Konfiguration des Wendelstein 7-X dargestellt. In der Graphik darunter sieht man gemessene Flussflächen des Wendelstein 7-AS: Die Durchstoßpunkte der Feldlinien durch eine Ebene mit – an dieser Stelle – eher dreiecksförmigem Querschnitt werden durch ein fluoreszierendes Medium in der Ebene sichtbar gemacht. In Falschfarben grün und braun dargestellte Punkte wurden vor und nach im Verlauf von 14 Jahren durchgeführten über 50.000 Plasmaexperimenten gemessen und zeigen, dass die modulare Spulenanordnung durch diese Belastungen nicht verändert wurde.[3]
Im Allgemeinen kommt ein Plasmateilchen jedem Punkt der Flussfläche bei seiner Bewegung beliebig nahe. Ausnahmen sind Flussflächen, auf denen die Verdrillung (Rotationstransformation) dazu führt, dass sich Feldlinien nach einigen wenigen Umläufen in sich selbst schließen. Solche „rationale Flussflächen“ sind empfindlich gegen geringfügige Magnetfeldstörungen, die dort zu inselartigen Magnetfeldstrukturen führen können, wie sie in der Abbildung rechts am Rand des Einschlussgebiets markiert sind. Solche festen oder auch dynamisch sich ausbildenden Inseln stellen Schwachpunkte bzw. Löcher in diesem magnetischen Käfig dar und können zu einem Verlust des Plasmas führen.
Die Magnetfelder für den Plasmaeinschluss erfordern starke Ströme (Größenordnung 20 kA) in großen Spulen. Die Stromstärke bestimmt den erreichbaren Plasmadruck. In einer Kraftwerksanlage müsste ein Plasmadruck von mehreren bar erreicht werden; dies ist mit Spulen aus geeigneten Supraleitern erreichbar.[4]
Einige neuere Konfigurationen toroidaler Maschinen sind der „Reversed Field Pinch“ und das „schwebende Dipol-Experiment“.
Kompakte Tori
Kompakte Tori, z. B. der Spheromak und der FRC (Field-Reversed Configuration), versuchen die guten Einschlusseigenschaften geschlossener magnetischer Flächen mit der Einfachheit von Maschinen ohne zentrale Spule zu kombinieren.
Lawson-Kriterium nicht erreicht
Die plasmaphysikalische Entwicklungsarbeit verfolgt grundsätzlich das Ziel, dem Lawson-Kriterium nahezukommen. Stacey[5] nennt dies bildhaft den „heiligen Gral“ der Plasmaforschung; ein Plasma würde in diesem Zustand ohne äußere Energiezufuhr „brennen“.
Bei den Versuchen, Teilchendichte, Temperatur und Energieeinschlusszeit des Plasmas entsprechend hochzutreiben, geraten alle genannten Konzepte in Schwierigkeiten. Manchmal wird der magnetische Einschluss mit dem Versuch verglichen, einen Luftballon gleichmäßig zusammenzuquetschen – immer wieder wird die Luft den Ballon an neuen Stellen ausstülpen. Solche Instabilitäten spielen eine wichtige Rolle, denn sie können dazu führen, dass das Plasma aus dem Einschlussbereich ausbricht und in Kontakt mit der Gefäßwand kommt. Wenn dies geschieht, werden schwere Teilchen (z. B. Kohlenstoff oder Eisen) aus der Wand des Gefäßes (Stahl oder andere Metalle) herausgelöst („Sputtering“ oder Zerstäubung), mischen sich mit dem Plasma und setzen seine Temperatur über Emission von Bremsstrahlung herab. Eine sehr wichtige Rolle spielt die Turbulenz: sie führt zum Transport von Teilchen und Energie aus dem Plasma heraus, was die Energieeinschlusszeit verringert.
Seit den 1990er-Jahren wurden beachtliche Fortschritte erzielt, sowohl bei der Annäherung der drei beteiligten Werte für Teilchendichte, Temperatur und Energieeinschlusszeit an die für „brennende“ Plasmen nötigen Größen als auch beim wissenschaftlichen Verständnis der beteiligten Prozesse. In JET-Experimenten konnten kurzzeitig bis zu 16 Megawatt Fusionsleistung erreicht[6] und das Verhalten der Heliumkerne (Alpha-Teilchen) in schwach brennenden Plasmen untersucht werden.
Elektromagnetische Wellen können in das Plasma injiziert und dazu verwendet werden, die Trajektorien von Plasmateilchen zu beeinflussen und Ströme zu treiben, die das Plasma einschließende Magnetfelder erzeugen. Diese und andere Erkenntnisse und Fortschritte der Plasmaforschung wurden größtenteils durch Experimente an Tokamaks gewonnen.
Fusion mit Netto-Energiegewinn ohne Erreichen des Lawson-Kriteriums
Die Lawson-Bedingung ist notwendig für das Funktionieren von Kernwaffen und Trägheitsfusions-Reaktoren. Beim magnetischen Einschlusskonzept muss sie nicht erfüllt sein, weil es hier möglich ist, das Plasma laufend weiter zu heizen, während es Fusionsenergie liefert. Notwendig für einen Netto-Energiegewinn ist nur, dass die nutzbare Fusionsleistung die zugeführte Heizleistung übersteigt; dies wird in der Literatur – auch für andere Einschlussmethoden – manchmal als Scientific break-even bezeichnet.[7][8] Dieser Fall soll erstmals mit ITER realisiert werden. Man kann die Fusionsleistung mit der Zusatzheizleistung im Sinne eines Verstärkungsfaktors in Beziehung setzen:
- .
Das erfüllte Lawson-Kriterium entspräche . In der Anlage JET wurde 1997 erreicht. ist der genannte scientific break-even. Der nächste „Meilenstein“ an diesem Entwicklungsweg wäre der engineering break-even, also eine Fusionsleistung, die den gesamten Eigenverbrauch des Kraftwerks einschließlich Kühlung usw. übersteigt.[9][10] Das für eine insgesamt wirtschaftliche Energiegewinnung nötige dürfte jenseits von 10 liegen.[5]
Auf den Wert ≈ 10 ist ITER ausgelegt. Viel höhere Werte sind mit der Technologie von ITER nicht kraftwerkstauglich realisierbar, denn die Heizsysteme sind dort auch für die Kontrolle des inhärent instabilen Plasmas notwendig.
Auch spätere Leistungsreaktoren wird man voraussichtlich so auslegen, dass das Lawson-Kriterium nicht erfüllt wird, sondern eine schwache Zusatzheizung von beispielsweise wenigen Prozent der Fusionsleistung nötig bleibt, um eine zusätzliche Möglichkeit zur Steuerung zu behalten.[5]
Literatur
- Friedrich Wagner: Auf den Wegen zum Fusionskraftwerk – Organisierter und selbstorganisierender magnetischer Einschluss. Physik Journal 8 (2009), Nr. 8/9, S. 35–41
- Weston M. Stacey: Fusion. An Introduction to the Physics and Technology of Magnetic Confinement Fusion. Wiley-VCH, 2010, ISBN 978-3-527-40967-9, eingeschränkte Vorschau in der Google-Buchsuche.
- C. M. Braams and P. E. Stott: Nuclear Fusion. Half a Century of Magnetic Confinement Fusion Research. IOP Publishing, Bristol 2002, ISBN 0-7503-0705-6.
Weblinks
Quellen
- Resonator-Podcast der Helmholtz-Gemeinschaft: Tokamak und Stellarator (Folge 30, 25. April 2015)
- http://www.ipp.mpg.de/de/aktuelles/presse/pi/2015/12_15
- M. Otte, R. Jaenicke: Magnetic flux surface measurements at Wendelstein W7-AS. (pdf; 3,2 MB) (Nicht mehr online verfügbar.) In: Stellarator News - Issue 100. James A. Rome at Oak Ridge National Laboratory, September 2005, S. 2–5, archiviert vom Original am 14. Juli 2016; abgerufen am 14. Juli 2016 (englisch). Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.
- Dennis Whyte et al. (MIT): Smaller & Sooner: How a new generation of superconductors can accelerate fusion’s development. Fusion Power Associates 2012, 31st Annual Meeting and Symposium, Washington, DC, Dezember 2012.
- Stacey, Fusion (s. Literaturliste), Seite 9
- M.Keilhacker, JET Deuterium-Tritium Results and their Implications.Webseite von EUROfusion. Abgerufen am 16. August 2016.
- J. S. Brzosko ei al.: Comments on the feasibility of achieving scientific break-even with a plasma focus machine. In: E. Panarella (Hrsg.): Current trends in International Fusion Research, Plenum Press, 1997
- S.A. Slutz et a.: Subignition fusion yields generated by fast heating of compressed deuterium-tritium and break-even scaling. Physics of Plasmas Band 11 (2004) Seite 3483, doi:10.1063/1.1753574
- J. Hiwatari et al.: Plasma performance required for a tokamak reactor to generate net electric power. Journal of Plasma and Fusion Research Band 78, No.10 (2002) Seite 991,
- J. Hiwatari et al.: Forthcoming Break-Even Conditions of Tokamak Plasma Performance for Fusion Energy Development. Journal of Plasma and Fusion Research Band 81, No.11 (2006) Seite 903–916,