Stufentheorie (Harmonik)

Die Stufentheorie, von Jacob Gottfried Weber (1779–1839) entwickelt und später von Ernst Friedrich Richter (1808–1879) ausgebaut, ist ebenso wie die Ende des 19. Jahrhunderts von Hugo Riemann (1849–1919) begründete Funktionstheorie ein Mittel zur beschreibenden Analyse der Harmonik eines Musikstückes. Beide Systeme haben sich bis in die heutige Zeit mit Modifikationen und Erweiterungen erhalten.

Mit Hilfe der Stufentheorie lässt sich der harmonische Bauplan eines Stückes verallgemeinernd veranschaulichen, so dass Vergleiche zu Stücken in anderen Tonarten einfacher werden, da die Symbole tonartunabhängig gelten. Gleichzeitig stellt die Stufentheorie umgekehrt harmonische Phrasen (Wendungen) bereit, die sich auf sämtliche Tonarten übertragen lassen.

Grundlagen

Die Stufentheorie geht von den Stufen derjenigen Tonleiter aus, die das Tonmaterial der Grundtonart des Stückes bereitstellt. Sie wurde ursprünglich entwickelt für diatonische Tonleitern wie Dur, Moll oder Kirchentonarten. Die hier folgenden Beispiele beziehen sich auf solche Tonleitern. Eine Stufentheorie ist aber grundsätzlich auch für jegliche andere (traditionelle oder neu erfundene) Skala wie Pentatonik, Ganztonleitern etc. möglich.

Nummerierung

Die Tonstufen der jeweiligen Tonleiter werden mit römischen Zahlen nummeriert. Die Nummerierung ist somit relativ zum Grundton und vermeidet absolute Tonnamen.

Am Beispiel einer C-Dur-Tonleiter:

Namensgebung

Neben diesen Nummern werden auch die aus der Funktionstheorie bekannten Namen verwendet. Die erste Stufe (Grundton oder Prime) wird Tonika genannt, die fünfte Stufe (Quinte) heißt Dominante, die vierte Stufe (Quarte) heißt Subdominante. Daneben gibt es die parallelen Dreiklänge: auf der dritten Stufe (Terz) die Dominantparallele, die zweite Stufe (Sekunde) heißt Subdominantparallele und die sechste Stufe (Sexte) heißt Tonikaparallele.

Dreiklänge für Dur-Tonleitern

Über jeder dieser Stufen lässt sich nun ein Dreiklang konstruieren, indem zwei Terzen darüber geschichtet werden. Die dazu benötigten Töne entstammen ebenfalls dem Material der Tonleiter, sie sind leitereigen.

Am Beispiel einer C-Dur-Tonleiter:

Aufgrund der verschiedenen Terzabstände innerhalb der Akkorde entstehen hier drei verschiedene Arten von Dreiklängen, wobei bei Dur und Moll das Rahmenintervall unverändert bleibt.

Dur (große Terz – kleine Terz) – Stufen I, IV und V
Moll (kleine Terz – große Terz) – Stufen II, III und VI
vermindert (kleine Terz – kleine Terz) – Stufe VII

Zum Beispiel beschreibt eine II in jeder beliebigen Dur-Tonart immer einen Molldreiklang, nämlich denjenigen Dreiklang, der mit leitereigenen Tönen über der zweiten Stufe der jeweiligen Tonleiter gebildet wird.

Dreiklänge für Moll-Tonleitern

Betrachtet man die Akkordbildung für (natürliches) Moll (hier c-Moll), ergibt sich folgende Verteilung:

Moll - Stufen I, IV und V
Dur - Stufen III, VI und VII
vermindert - Stufe II

Erweiterung der Stufensymbole

Eine Erweiterung der römischen Zahlen wird dann nötig, wenn

den Dreiklängen ein vierter, fünfter,... Ton hinzugefügt wird
ein Ton des Dreiklangs durch einen anderen ersetzt wird
ein anderer als der Grundton tiefster Ton (=Basston) ist
ein Ton des Dreiklangs nicht leitereigen ist (=Fremdton).

Im Folgenden werden diese Fälle erläutert:

Vierklang, Fünfklang etc.

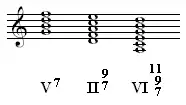
Es ist möglich, den Ausgangsdreiklang durch Aufschichtung weiterer Terzen zu erweitern. Das Ergebnis sind Vierklänge, Fünfklänge etc. Dies wird mit (arabischen) Zahlen angezeigt, die rechts oben (wie ein Exponent) neben die römische Zahl geschrieben werden. Ihr Wert gibt das Intervall des zusätzlichen Tones in Bezug auf den Grundton des Dreiklangs an: eine 7 bezeichnet die Septime, eine 9 die None usw. Da die Intervalle 1 (Grundton), 3 (Terz) und 5 (Quinte) ohnehin im Dreiklang enthalten sind, werden diese Töne nicht bezeichnet, sofern sie leitereigen sind.

In C-Dur:

Umkehrungen

Die klassische Stufentheorie kombiniert bei der Kennzeichnung von Akkordumkehrungen die grundton-orientierte Deutung der Stufe mit dem basston-orientierten Bezifferungssystem des Generalbass. So steht

eine hochgestellte 6 für Sextakkord-Stellung bzw. 1. Dreiklangsumkehrung bzw. Terzbass
eine hochgestellte 4 und 6 für Quartsextakkord bzw. 2. Dreiklangsumkehrung bzw. Quintbass
eine hochgestellte 5 und 6 für Quintsextakkord bzw. 1. Vierklangsumkehrung
eine hochgestellte 3 und 4 für Terzquartakkord bzw. 2. Vierklangsumkehrung
eine hochgestellte 2 für Sekundakkord bzw. 3. Vierklangsumkehrung bzw. Septimbass

Da dieses Bezeichnungssystem „um die Ecke gedacht“ ist und durch die Kombination unterschiedlicher Sichtweisen Schwierigkeiten auftreten bei gleichzeitiger Kennzeichnung von Akkordumkehrungen und Zusatztönen, verwenden einige Stufentheoretiker auch das Bezifferungssystem der Funktionstheorie, das Basstöne durch unterstellte Ziffern kennzeichnet. Diese Ziffern sind wie die Stufendeutung grundton-orientiert und benennen das Intervall des Basstons im Verhältnis zum Akkordgrundton:

Tonersetzung

Gekennzeichnet werden auch Töne, die einen Dreiklangston ersetzen. Das Ergebnis sind Vorhaltakkorde, bei denen konzeptuell ein dreiklangsfremder Ton vorher gehalten wird, bevor er dann in den dreiklangseigenen Ton zurückgeführt wird. Ob diese „Auflösung“ tatsächlich stattfindet, ist vom Stil der Musik und von der konkreten Aufgabe des Akkords abhängig. Bei einer Auflösung werden im Zielakkord die sonst nicht notierten Akkordstufen 3, 5 und 8 notiert, wie in den folgenden Beispielen zu sehen ist.

Bei Bezifferung der dreiklangsfremder Töne gilt: 4 ersetzt 3 (d. h., bei Bezeichnung nur mit der 4 enthält der Akkord keinen Terzton), 6 ersetzt 5, 9 ersetzt 8 (oktavierter Grundton). Wegen dieser Regel müssen gelegentlich die sonst nicht notierten Ziffern 3, 5 und 8 ebenfalls angegeben werden, wie beim hier rot markierten Akkord, wo sowohl die Quint wie die Sext erklingen; IV⁶ würde hingegen den Akkord f-a-d ohne Quint c bezeichnen.

In C-Dur:

Da jeder Akkord aus mehreren Dreiklangstönen besteht, sind auch andere Möglichkeiten der Bezeichnung der obenstehenden Akkorde möglich. So wird der drittletzte, rot markierte Akkord (f-a-c-d) auch als II⁷ gekennzeichnet, da manche Stufentheoretiker ihn je nach Kontext auch als Septakkord der II. Stufe in erster Umkehrung betrachten. Die Auswahl der Bezeichnung kann dann etwa gemäß der zugrundeliegenden Terzschichtung oder auch aufgrund der Harmonieabfolge verschieden gewählt werden, wodurch die Stufenbezeichnung eine zusätzliche Deutung eines Akkordes vornimmt. So kann man die Bezeichnung II⁷ für den f-a-c-d-Akkord als nächstliegende sehen sowohl deswegen, weil sie den Akkord in der als grundlegend angenommenen Terzschichtung bezeichnet, als auch bezüglich der Auflösung zur fünften Stufe hin, die regulär im Sinne eines Quintsextakkords der zweiten Stufe erfolgt. Eine Deutung desselben Akkordes als vierte Stufe mit hinzugefügter Sexte (Sixte ajoutée), wie im Beispiel gezeigt, bietet sich dann an, wenn die Sexte aufwärts geführt wird und die Auflösung im Sinne eines Plagalschlusses direkt zur ersten Stufe hin erfolgt.

Fremdton

Neben der Tonersetzung durch leitereigene Töne kommt es auch vor, dass Töne eines Dreiklangs durch nicht leitereigene Fremdtöne ersetzt werden. Selten ist dabei die Quinte des Dreiklangs betroffen, fast nie der Grundton, dafür die Terz umso häufiger. Dies rührt daher, dass die Terz (groß oder klein) den Dreiklang in Dur oder Moll einordnen lässt. Will man zum Beispiel die V. Stufe einer Molltonleiter (ursprünglich ist dieser Dreiklang ein Moll-Dreiklang, s. o.) mit dem für diese Stufe charakteristischen Leitton versehen, um die dominantische Wirkung zu verstärken, muss die (kleine) Terz um einen Halbton erhöht werden. In der Notation wird hierzu eine 3 mit Kreuz (♯) rechts neben die römische Zahl gestellt. Da die Veränderung der Terz die häufigste dieser Art ist, wird oft die 3 weggelassen und nur ein Kreuz geschrieben. Meint man einen anderen Ton als die Terz, so ist dieser in jedem Fall zu bezeichnen. Eine Erniedrigung des Tones wird analog mit einem ♭ gekennzeichnet.

In c-Moll:

Verwendung

Anders als die Funktionstheorie beschreibt die Stufentheorie keine Spannungsbeziehungen zwischen Akkorden. Da sie aber wesentlich elementarer aufgebaut ist, hat sie einen Vorteil: Mit ihrer Hilfe lassen sich manche Akkorde in Relation zu anderen Akkorden beschreiben, ohne dass wie in der Funktionsharmonik auf jeden Fall eine Funktion zugeordnet werden muss, besonders wenn diese Funktion selbst schon fraglich ist. Für die Stufenlehre ist z. B. im Rahmen von C-Dur der Dreiklang e-g-h als III. Stufe eindeutig und vollständig benannt, wogegen er in der Funktionstheorie je nach Zusammenhang entweder als Tonikagegenklang oder als Dominantparallele zu deuten ist.

Sinnvoll ist der Einsatz der Stufentheorie in vielen Musikgattungen insbesondere, wenn man Sequenzen beschreiben möchte: Die Intervallbeziehungen der Akkorde untereinander lassen sich dann leichter erkennen und zeigen oft musikalische Zusammenhänge über größere Strecken, die bei der Verwendung von Funktionen nicht so offensichtlich zutage treten.

Wenn in der musikalischen Praxis eine musikalische Analyse nicht so wichtig ist wie eine schnell erfassbare, aber dennoch abstrakte Beschreibung einer Akkordfolge, ist die Stufentheorie (oder eher eine Stufennotation) oft besser geeignet als einerseits konkrete Akkordsymbole, andererseits abstrakte Funktionsbezeichnungen. So ist im Jazz und der Unterhaltungsmusik allgemein die Harmoniefolge „II-V-I“ als eine der meistverbreiteten Schlusswendungen bekannt.

Beispiel einer Analyse

Analyse

Ein einfaches Beispiel, um anhand der Stufentheorie eine Sequenz zu zeigen und gleichzeitig die verschiedenen Einsatzmöglichkeiten von Stufen- und Funktionstheorie zu erläutern, sei ein Abschnitt aus Mozarts Zauberflöte aus dem Quintett Nr. 5: Klangbeispiel im MIDI-Format (2 kB)

Zunächst zu den ersten drei Takten, die als Sequenz gekennzeichnet sind:

Die ersten zwei Klänge I-V stehen im Abstand einer Quinte (Differenz vier Stufen). Ebenso verhalten sich die folgenden Klänge VI-III und IV-I. Alternativ könnte man schreiben VI-X statt VI-III sowie IV-VIII statt IV-I. Die Stufen X und VIII existieren jedoch nicht und dienen hier nur der besseren Veranschaulichung der Differenzen.

Die Klangfolge des ersten Taktes wird also von einem jeweils anderen Ausgangspunkt wiederholt, sie wird sequenziert.

Diese Ausgangspunkte am Beginn jeden Taktes (I-VI-IV) haben den Abstand einer Terz (Differenz zwei Stufen), alternativ VIII-VI-IV. In Worte gefasst hieße das: Der aufwärts gerichtete Quintsprung I-V wird in der Sequenz zweimal um eine Terz versetzt wiederholt. Diese Folge wird sogar im vierten Takt scheinbar fortgesetzt, denn der Basston c wäre der Grundton der sequenzgerecht erscheinenden II. Dazu unten mehr.

Das Erscheinen dieses Tons wird noch zwingender herbeigeführt durch die schrittige Basslinie – sie bewegt sich in Sekunden abwärts und lässt die Stufen V, III und I als Sextakkorde erscheinen.

Wem beim Abhören des Beispiels die klangliche Nähe zu Pachelbels berühmtem Kanon aufgefallen ist, findet dies bei der Analyse desselben bestätigt: Die Akkordfolge D-A-h-fis-G-D-G-A liefert in D-Dur die Stufen I-V-VI-III-IV-I-IV-V. Obwohl das Stück in einer anderen Tonart steht, sieht man auf den ersten Blick, dass sich die ersten sechs Klänge genauso verhalten wie bei Mozart, das Sequenzmodell ist das gleiche. Unterschiede: bei Pachelbel handelt es sich immer um Dreiklänge in Grundstellung und die Kadenz am Schluss der Phrase wird anders behandelt.

Betrachtet man nun – zurück bei Mozart – für diesen Abschnitt die Funktionen, wird schnell ersichtlich, warum sich für diese Takte zur Beschreibung eher die Stufentheorie eignet: Zwar scheint am Anfang eine gewisse Regelmäßigkeit zu herrschen, dies suggeriert die elementare Folge T-D-T-D. Doch spätestens mit dem Erscheinen der Subdominante im dritten Takt ist diese Regelmäßigkeit zerstört. Des Weiteren ist die Beschreibung des vierten Klanges als Dominantparallele sehr irreführend, da er in dieser Form keinen dominantischen Charakter mehr hat. Zudem wäre die Folge D-S im strengen Sinne regelwidrig aufgrund der umgekehrten Spannungsempfindung. (Trotzdem kommt diese Folge zum Beispiel in Popmusik oft vor, da diese häufig mit Plagalschlüssen arbeitet: D-S-T klingt hier sehr geläufig)

Der vierte Takt:

Ist die Sequenz der ersten drei Takte zum Ende gekommen, wird der Basston c (Grundton der II Stufe) umgedeutet zur Terz der VII Stufe bzw. zur Quinte der Dominante. Mozart verlässt hier bewusst das Sequenzmodell, um eine weitere Bewegung in der gleichen Richtung abzufangen. Die sich anschließende Kadenz endet mit einem Halbschluss auf der Dominante. Dies ist nicht ungewöhnlich, da das Prinzip Spannung-Entspannung innerhalb eines achttaktigen Satzes eher die Norm ist. An diesem Punkte sind Stufen- und Funktionstheorie fast gleichwertig, wenn man davon ausgeht, dass die fünfte Stufe als spannungsreicher Klang aufgefasst wird. Hier spielt allerdings schon die Erfahrung mit hinein, dass diese Stufe die Dominante bildet, es handelt sich also eher um eine gedankliche Kombination der beiden Theorien.

Die zweite Hälfte:

In diesem Abschnitt wäre wahrscheinlich der funktionalen Beschreibung aus verschiedenen Gründen der Vorzug zu geben. Am Anfang signalisiert das lange Verweilen in der Dominante die Ausweichung in dieselbe; der Trugschluss in die Tonikaparallele als absonderliches Ereignis erscheint ebenso deutlicher als die Folge V-VI; das Erscheinen der Subdominante im siebten Takt leitet klar den zweiten „Versuch“ ein, die Tonika zu etablieren, worauf sich eine vollständige Kadenz mit Ganzschluss anschließt als stereotype Folge T-S-D-T.

Man sieht, wie sich beide Theorien gut ergänzen und sowohl Vor- als auch Nachteile haben, die sich leicht mit der jeweils anderen Theorie umgehen lassen.

Literatur

Reinhard Amon: Lexikon der Harmonielehre. Doblinger, Wien 2005. ISBN 3-476-02082-7
Richard Graf, Barrie Nettles: Die Akkord-Skalen-Theorie & Jazz-Harmonik. Advance Music, Rottenburg/N. 1997, ISBN 3-89221-055-1
Paul Hindemith: Aufgaben für Harmonieschüler. Schott, Mainz 1949, 1985, 1990 (Nachdr.). ISBN 3-7957-1602-0
Carl Dahlhaus: Untersuchungen über die Entstehung der harmonischen Tonalität. Bärenreiter, Kassel 1967, 1988. ISBN 3-7618-0908-5
Frank Haunschild: Die neue Harmonielehre. Ama, Brühl 1988, 1997. ISBN 3-927190-00-4
Axel Kemper-Moll: Jazz & Pop Harmonielehre. Voggenreiter, Bonn 2005. ISBN 3-8024-0349-5
Abi von Reininghaus: In Vivo Guitar. Harmonielehre für Gitarre. Voggenreiter, Bad Godesberg 1994. ISBN 3-802-40226-X
Simon Sechter: Praktische Generalbaß-Schule. 1835, Leuckart, Leipzig 1850.
Simon Sechter: Die Grundsätze der musikalischen Komposition. Breitkopf & Härtel, Leipzig 1853–54.
Frank Sikora: Neue Jazz-Harmonielehre. Schott, Mainz 2003. ISBN 3-7957-5124-1
Gerald Smrzek: The Book of Chords. Edition Canticum, Wien 2005.
Joe Viera: Grundlagen der Jazzharmonik, universal edition, 1980

Weblinks

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.