Fünfzehneck
Das Fünfzehneck oder Pentadekagon ist eine geometrische Figur und ein Vieleck (Polygon). Es ist bestimmt durch fünfzehn Eckpunkte und deren fünfzehn Verbindungen namens Strecken, Seiten oder Kanten.
Variationen
Das Fünfzehneck ist darstellbar als:
- konkaves Fünfzehneck, in dem mindestens ein Innenwinkel größer als 180° ist. Ein Fünfzehneck kann höchstens sieben solche Winkel haben.
- konvexes Fünfzehneck, in dem alle Innenwinkel kleiner als 180° sind. Ein konvexes Fünfzehneck kann regelmäßig oder unregelmäßig sein.
- Sehnenfünfzehneck, in dem alle Ecken auf einem gemeinsamen Umkreis liegen, aber die Seitenlängen möglicherweise ungleich sind.
- regelmäßiges Fünfzehneck: Es ist bestimmt durch fünfzehn Punkte auf einem virtuellen oder realen Kreis. Die benachbarten Punkte haben zueinander stets den gleichen Abstand und sind mittels aneinandergereihten Strecken, auch Seiten oder Kanten genannt, verbunden.
- regelmäßiges überschlagenes Fünfzehneck: Es ergibt sich, wenn beim Verbinden der fünfzehn Eckpunkte jedes Mal mindestens einer übersprungen wird und die somit erzeugten Sehnen gleich lang sind. Notiert werden solche regelmäßigen Sterne mit Schläfli-Symbolen , wobei die Anzahl der Eckpunkte angibt und jeder -te Punkt verbunden wird.
- Es gibt nur drei regelmäßige Fünfzehnstrahlsterne.
- Die „Sterne“ mit den Symbolen {15/3} und {15/12} sind regelmäßige Fünfecke, {15/5} und {15/10} gleichseitige Dreiecke und {15/6} und {15/9} regelmäßige Pentagramme.
- Regelmäßige Fünfzehnstrahlsterne



Regelmäßiges Fünfzehneck
Das regelmäßige Fünfzehneck ist nach Carl Friedrich Gauß und Pierre-Laurent Wantzel ein konstruierbares Polygon, da die Anzahl seiner Seiten als Produkt einer Zweierpotenz mit paarweise voneinander verschiedenen Fermatschen Primzahlen () darstellbar ist.[1] Wie beim regelmäßigen Fünfeck ist der Goldene Schnitt der maßgebende Baustein für eine Konstruktion mit Zirkel und Lineal.
Größen
| Größen eines regelmäßigen Fünfzehnecks | ||
|---|---|---|
| Innenwinkel |
| |
| Zentriwinkel (Mittelpunktswinkel) |
||
| Seitenlänge | ||
| Umkreisradius | ||
| Inkreisradius | ||
| Höhe | ||
| Flächeninhalt | ||
Mathematische Zusammenhänge
Innenwinkel
Die allgemeine Formel für Polygone liefert:
Dieser Wert lässt sich auch durch folgende Überlegungen herleiten:
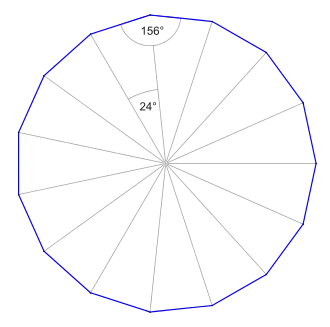
Das Fünfzehneck lässt sich in fünfzehn Dreiecke teilen, deren Seiten jeweils eine Seite des Fünfzehnecks und die Verbindungsstrecken seines Mittelpunktes mit den zwei Endpunkten der Seite sind. Die Winkel am Mittelpunkt des Fünfzehnecks addieren sich zu sein Zentriwinkel beträgt also Da die Winkelsumme in einem Dreieck immer beträgt und das Dreieck gleichschenklig und damit symmetrisch zur Halbierenden des Zentriwinkels ist, schließen die beiden unbekannten Winkel jeweils ein. Da das für alle fünfzehn Dreiecke gilt, addieren sich die beiden Winkel an einem Eckpunkt zu .
Zentriwinkel
Der Zentriwinkel oder Mittelpunktswinkel wird von zwei benachbarten Umkreisradien eingeschlossen. In der allgemeinen Formel ist für die Variable die Zahl einzusetzen.
Seitenlänge und Umkreisradius
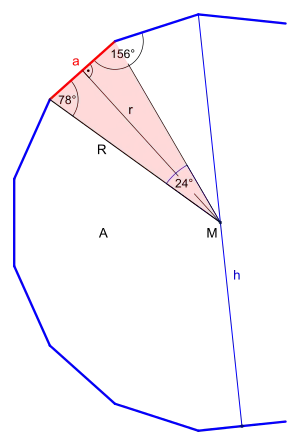
Wieder wird das Fünfzehneck in 15 kongruente Dreiecke zerlegt. Nimmt man die Hälfte eines solchen Dreiecks, also ein rechtwinkliges Dreieck mit den Seiten , und sowie mit dem halben Zentriwinkel so gilt
Aus dieser Beziehung folgt
Löst man nach auf, so erhält man
Algebraische Ausdrücke für bzw. finden sich in den Abschnitten Berechnung der Seitenlänge und Berechnung des Umkreisradius.
Inkreisradius
Auch der Inkreisradius lässt sich mithilfe eines halbierten Bestimmungsdreiecks ermitteln. Es ergibt sich
- .
Durch Multiplikation mit erhält man
und weiter
wegen
gilt auch
Algebraische Ausdrücke für bzw. finden sich im Abschnitt Berechnung des Inkreisradius.
Höhe
Die Höhe h eines regelmäßigen Fünfzehneckes ist die Summe aus In- und Umkreisradius, da die Verlängerung der Höhe eines Teilstückes über den Mittelpunkt des Fünfzehnecks hinaus auf einen Eckpunkt trifft.
Flächeninhalt
Der Flächeninhalt eines Dreiecks berechnet sich zu . Für eines der 15 Bestimmungsdreiecke ist die Höhe gleich dem Inkreisradius . Der Flächeninhalt des gesamten Fünfzehnecks beträgt also
Zusammen mit dem in Berechnung des Inkreisradius hergeleiteten Ausdruck für folgt daraus
Konstruktion mit Zirkel und Lineal bei gegebenem Umkreis
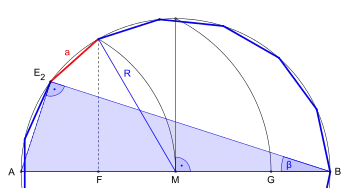
In der hier dargestellten Konstruktion werden ein gleichseitiges Dreieck (Schritte 1–3) und die ersten vier Punkte eines regelmäßigen Fünfecks (Schritte 4–6) in den gegebenen Umkreis eingepasst. ist dann die Seite eines regelmäßigen Fünfzehnecks im gegebenen Umkreis. Diese Art der Konstruktion beschrieb schon Euklid in seinem Werk Elemente (Die Stoicheia) im IV Buch; die Konstruktionsdetails des Dreiecks und Fünfecks weichen jedoch von seiner Konstruktion ab.[2] Das Bestimmen der ersten Seite des Fünfzehnecks entspricht der Darstellung von Johannes Kepler[3].
bezeichnet die Strecke zwischen den Punkten und
Ist ein Kreis k1 (der Umkreis um das entstehende Fünfzehneck) um den Mittelpunkt M gegeben, lässt sich ein regelmäßiges Fünfzehneck konstruieren durch:
- Zeichnen eines Durchmessers; Schnittpunkte mit k1 sind A und B
- Konstruktion eines Radius, der orthogonal zu AB steht; Schnittpunkt mit k1 ist C
- Konstruktion eines Kreisbogens um A mit dem Radius AM; Schnittpunkte mit k1 sind E1 und E6
- Zeichnen von E1E6; Schnittpunkt mit AB ist F
- Zeichnen eines Kreisbogens um F mit dem Radius FC; Schnittpunkt mit AB ist G
- viermaliges Abtragen der Strecke CG auf k1 ab B entgegen dem Uhrzeigersinn; Schnittpunkte mit k1 sind E14, E2, E5, und E8; die Verbindung der Eckpunkte E1 mit E2 ergibt die erste Seite des entstehenden Fünfzehnecks
- achtmaliges Abtragen der Sehne E1E2 von k1 auf k1 ab E2 entgegen dem Uhrzeigersinn; die Schnittpunkte mit k1 sind die restlichen Eckpunkte E3, E4, E7, E9, E10, E12, E13 und E15 des Fünfzehnecks
- Verbinden der so gefundenen Punkte.
Berechnung der Seitenlänge
Die in obiger Tabelle angegebene Formel für die Seitenlänge leitet sich wie folgt her:
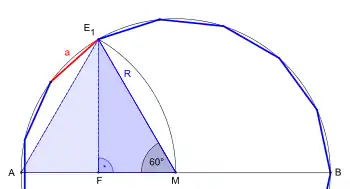
- (Umkreisradius)
- nach Konstruktion, Schritt 3
- Es gilt nach dem Satz des Pythagoras:
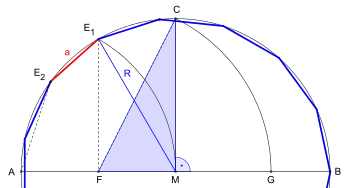
Rechtwinkliges Dreieck
- Es gilt nach dem Satz des Pythagoras:
- nach Konstruktion, Schritt 5
Rechtwinkliges Dreieck
- bezeichnet den von und eingeschlossenen Winkel :
- Nach dem Satz des Thales ist das Dreieck rechtwinklig, wieder gilt nach dem Satz des Pythagoras:
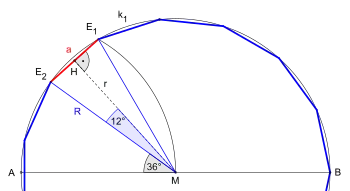
- (Seitenlänge)
- aus (4.4)
- aus (4.5)
Zur Berechnung der Seitenlänge benötigt man den Wert von , der sich mithilfe der Additionstheoreme berechnen lässt:
Damit ergibt sich für die Seitenlänge:
Berechnung des Inkreisradius
Die in obiger Tabelle angegebene Formel für den Inkreisradius leitet sich wie folgt her:

- aus Mathematische Zusammenhänge, Inkreisradius
- aus Berechnung der Seitenlänge (6.1)
Zur Berechnung des Inkreisradius benötigt man für den Term zuerst den Wert von der sich mithilfe der Additionstheoreme berechnen lässt:
Die folgende hergeleitete Beziehung lässt sich zur Umformung von Rechenausdrücken verwenden.
denn es gilt
Zur abschließenden Berechnung des Inkreisradius wird nun der Wert von ermittelt.
- Aus Gründen der besseren Übersicht sind acht dazwischenliegende Berechnungsschritte nur im Bearbeitungsmodus sichtbar!
Damit ergibt sich für den Inkreisradius
Konstruktion mit Zirkel und Lineal bei gegebener Seitenlänge
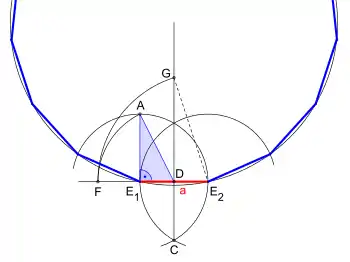
Die Konstruktion ist nahezu gleich mit der des Fünfecks bei gegebener Seitenlänge, auch darin gelingt die Darstellung mittels Verlängerung der Seite und einer damit generierten Strecke, hier die nach dem Goldenen Schnitt, äußere Teilung geteilt ist.
bezeichnet die Strecke zwischen den Punkten und
Ist eine Seite eines Fünfzehnecks gegeben, lässt sich ein regelmäßiges Fünfzehneck konstruieren durch:
- Bezeichnen der Streckenenden mit E1 und E2; beide sind Eckpunkte des entstehenden Fünfzehnecks
- Verlängern der Strecke E1E2 ab E1 um ca. einer Länge dieser Strecke
- Zeichnen eines Kreisbogens um E1 mit dem Radius E1E2
- Konstruktion einer Senkrechten zur Strecke E1E2 ab E1; Schnittpunkt mit dem Kreisbogen um E1 ist A
- Zeichnen eines Kreisbogens um E2 mit dem Radius E1E2; Schnittpunkte mit Kreisbogen um E1 sind B und C
- Zeichnen einer geraden Linie ab C durch B (Mittelsenkrechte von E1E2), die etwas mehr als dreimal so lang wie BC ist; Schnittpunkt mit E1E2 ist D
- Zeichnen eines Kreisbogens um D mit dem Radius DA; Schnittpunkt mit Verlängerung der Strecke E1E2 ist F
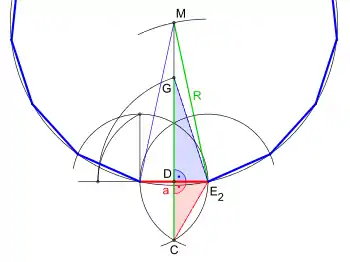
- Zeichnen eines Kreisbogens um E2 mit dem Radius E2F; Schnittpunkt mit der geraden Linie (ab C durch B) ist G
- Zeichnen eines kurzen Kreisbogens um E2 mit dem Radius CG; Schnittpunkt mit Verlängerung der Strecke CB ist M, der Mittelpunkt des Umkreises des entstehenden Fünfzehnecks
- Zeichnen des Umkreises k1 um M mit dem Radius ME2; Schnittpunkt mit dem Kreisbogen um E2 ist Eckpunkt E3
- elfmaliges Abtragen der Sehne E1E2 von k1 auf k1; Schnittpunkte mit k1 sind die Eckpunkte E3–15 des Fünfzehnecks
- Verbinden der so gefundenen Eckpunkte.
Berechnung des Umkreisradius
Die in obiger Tabelle angegebene Formel für den Umkreisradius leitet sich wie folgt her:
(Seitenlänge)
Rechtwinkliges Dreieck
- Es gilt nach dem Satz des Pythagoras:
- nach Konstruktion, Schritt 7
- nach Konstruktion, Schritt 8
Rechtwinkliges Dreieck
- Es gilt nach dem Satz des Pythagoras:
Rechtwinkliges Dreieck
- Es gilt nach dem Satz des Pythagoras:
Nach Konstruktion, Schritt 9 gilt für den Umkreisradius
Der Goldene Schnitt im Fünfzehneck
Sowohl in der Konstruktion bei gegebenem Umkreis als auch in der bei gegebener Seitenlänge wird der Goldene Schnitt zur Bestimmung von Konstruktionselementen verwendet.
- In der Konstruktion bei gegebenem Umkreis teilt der Punkt die Strecke im Verhältnis des Goldenen Schnittes:
- In der Konstruktion bei gegebener Seitenlänge wird die Seite derart verlängert, dass sie die längere Strecke des Verhältnisses ist:
Siehe auch
Literatur
- H. Maser: Die Teilung des Kreises ..., Artikel 365., in Carl Friedrich Gauss' Untersuchungen über höhere Arithmetik, Verlag von Julius Springer, Berlin 1889; Göttinger Digitalisierungszentrum, Universität Göttingen; abgerufen am 15. März 2018.
Weblinks
- Eric W. Weisstein: Pentadecagon. In: MathWorld (englisch). abgerufen am 4. Oktober 2015.
Einzelnachweise
- Jürgen Köller: Regelmäßiges Vieleck. In: Mathematische Basteleien. 2005, abgerufen am 4. Oktober 2015.
- Johann Karl Friedrich Hauff: EUKLIDS ELEMENTE. DAS ERSTE BIS ZUM SECHSTEN, SAMMT DEM EILFTEN UND ZWOELFTEN BUCHE. neue academische Buchhandlung, Marburg 1807, S. 129 f. (eingeschränkte Vorschau in der Google-Buchsuche).
- Johannes Kepler: WELT-HARMONIK. XLIV. Satz., Seite des Fünfzehnecks, Seite 44, aus dem Internet Archive regeneriert. In: Google Books. R. OLDENBURG VERLAG 2006, übersetzt und eingeleitet von MAX CASPAR 1939, S. 401, abgerufen am 19. Juli 2019.