Ionosphärische Dynamoschicht
Die ionosphärische Dynamoschicht, ein Bereich in der Erdatmosphäre, befindet sich zwischen etwa 85 und 200 km Höhe und ist gekennzeichnet durch ein elektrisch leitendes ionosphärisches Plasma, das durch solare und lunare atmosphärische Gezeiten gegen die Kraftlinien des Erdmagnetfeldes bewegt wird und dabei elektrische Felder und Ströme induziert, genauso wie in einem technischen Dynamo die bewegte Spule, die sich gegen ein Magnetfeld bewegt. Das Magnetfeld solcher Ströme wird auf der Erdoberfläche als Schwankung des Erdmagnetfeldes gemessen. Diese Variationen werden Sq-Variationen (S = solar; q =quiet) und L-Variationen (l = lunar) genannt[1]. Die Gezeiten selbst werden durch unterschiedliche Sonneneinstrahlung in der Atmosphäre bzw. durch den gravitativen Einfluss des Mondes hervorgerufen.
Ein variierendes magnetosphärisches elektrisches Konvektionsfeld erzeugt zusätzliche elektrische Ströme innerhalb der ionosphärischen Dynamoschicht, die DP1- (die polaren Elektrojets) und die DP2-Ströme[2]. Des Weiteren gibt es einen polaren Ringstrom, der vom interplanetaren Magnetfeld abhängt.[3] Solche geomagnetischen Variationen gehören zum erdmagnetischen Außenfeld, dessen Amplituden selten 1 % des internen Hauptfeldes Bo erreichen.
Atmosphärische elektrische Leitfähigkeit
Radioaktives Gas aus dem Erdinneren und galaktische kosmische Strahlung ionisieren einen kleinen Teil der Luft innerhalb der unteren und mittleren Atmosphäre und machen das Neutralgas elektrisch leitend. Elektronen verbinden sich sehr schnell mit Neutralgaspartikeln und bilden negative Ionen. Die Ionen sind in der Regel einatomig. Die elektrische Leitfähigkeit hängt von der Mobilität der Ionen ab. Diese Mobilität ist proportional zur reziproken Luftdichte und wächst deshalb exponentiell mit der Höhe. Die Ionen bewegen sich mit dem Neutralgas, sodass die elektrische Leitfähigkeit isotrop, aber äußerst klein ist.[4]
Im Höhenbereich zwischen etwa 85 und 200 km – der Dynamoschicht – werden die solare Röntgen- und die extreme Ultraviolettstrahlung (XUV) nahezu vollständig absorbiert und dabei die Luft teilweise ionisiert. Es entstehen die unterschiedlichen Ionosphärenschichten. In diesem Höhenbereich sind die Elektronen bereits an das Erdmagnetfeld gebunden und gyrieren mehrfach um die Magnetfeldlinien, bevor sie mit Neutralgaspartikeln zusammenstoßen. Die Ionen dagegen bewegen sich im Wesentlichen mit dem Neutralgas. Die Folge ist eine anisotrope elektrische Leitfähigkeit. Die Leitfähigkeit parallel zum elektrischen Feld E heißt Pedersen-Leitfähigkeit. Pedersen-Ströme haben ohmsche Verluste und erzeugen damit Joule’sche Erwärmung. Die Leitfähigkeit senkrecht zu E und zum Erdmagnetfeld Bo ist die Hall-Leitfähigkeit. Die Komponente parallel zu Bo (Parallel-Leitfähigkeit) wächst weiter mit der Höhe. In der Nähe des erdmagnetischen Äquators erzeugt ein west-östliches elektrisches Feld einen vertikalen Hall-Strom, der nicht geschlossen ist. Dadurch wird ein vertikales Polarisationsfeld aufgebaut, das einen horizontalen Hall-Strom erzeugt. Dieser zusätzliche Hall-Strom verstärkt den Pedersen-Strom. Solche Verstärkung wird durch die Cowling-Leitfähigkeit beschrieben. Pedersen- und Hall-Leitfähigkeit erreichen ein Maximum in etwa 120 bis 140 km. Am Tage besitzen sie Zahlenwerte von ca. 1 mS/m. Nachts können diese Werte auf ein Zehntel zurückgehen. Die Werte der Leitfähigkeiten hängen von der Tageszeit, von der Breite, von der Jahreszeit und vom Elfjahreszyklus der Sonne ab. Die höhenintegrierten Leitfähigkeiten sind von der Größenordnung von 50 S, bzw. besitzen einen Widerstand von ca. 0,02 Ohm.[5]
In den Polarlichtzonen, die in ca. 70° bis 75° nördlicher und südlicher geomagnetischer Breite liegen, fallen hochenergetische Partikel aus der Magnetosphäre ein, die die Luft in ca. 110 bis 120 km Höhe zusätzlich ionisieren und damit Pedersen- und Hall-Leitfähigkeit erhöhen. Diese Leitfähigkeit wächst während starker erdmagnetischer Störungen.[2]
Oberhalb von etwa 200 km werden die Zusammenstöße zwischen Neutralgas und Plasma immer seltener, sodass sowohl positive Ionen wie Elektronen nur noch um die Magnetfeldlinien gyrieren oder senkrecht zu E und Bo driften können. Die Parallel-Leitfähigkeit wird so groß, dass die geomagnetischen Feldlinien elektrische Äquipotentiallinien werden. Es können also nur noch elektrische Felder orthogonal zu Bo existieren (siehe Magnetosphäre).
Atmosphärische Gezeiten
Atmosphärische Gezeiten sind großräumige atmosphärische Wellen, die durch reguläre differentielle Sonneneinstrahlung (solare Gezeiten) oder durch den gravitativen Einfluss des Mondes (lunare Gezeiten) angeregt werden. Die Atmosphäre verhält sich wie ein riesiger Wellenleiter, der unten (am Erdboden) geschlossen und nach oben offen ist. In solchem Wellenleiter kann eine unendlich große Zahl von Eigenwellen (Wellenmoden) erzeugt werden. Der Wellenleiter ist jedoch nicht perfekt, sodass sich nur Wellen mit großen horizontalen und vertikalen Dimensionen genügend entwickeln, um aus dem meteorologischen Rauschen herausgefiltert werden zu können. Diese Wellen sind Lösungen der Laplace-Gleichung. Sie heißen Hough-Funktionen und lassen sich durch Kugelfunktionen approximieren.[6]
Es gibt zwei Arten von Wellentypen: Wellen der Klasse I (auch Gravitationswellen genannt) und Wellen der Klasse II (Rotationswellen). Klasse-II-Wellen existieren nur auf Grund der Corioliskraft und verschwinden für Perioden kleiner als 12 Stunden. Die Eigenwellen sind entweder interne Wellen mit endlich großen vertikalen Wellenlängen, die Wellenenergie nach oben transportieren können, oder externe Wellen mit unendlich großen vertikalen Wellenlängen, deren Phasen konstant mit der Höhe sind. Die Amplituden interner Wellen wachsen exponentiell mit der Höhe. Externe Wellen dagegen können keine Wellenenergie transportieren, und ihre Amplituden nehmen außerhalb ihres Quellenbereiches exponentiell mit der Höhe ab. Jeder Wellenmode ist durch vier Zahlen charakterisiert: durch die zonale Wellenzahl n, die meridionale Wellenzahl m (die meridionale Struktur der Wellen wird mit wachsendem m immer komplexer), durch ihren Eigenwert (in Anlehnung an Ozeangezeiten auch äquivalente Tiefe genannt), und durch ihre Periode, im Falle der Gezeiten 12 Stunden (halbtägige Wellen) und 24 Stunden (ganztägige Wellen) etc. Die Moden werden durch das Zahlenduo (n, m) gekennzeichnet. Gerade Zahlen von n gelten für symmetrische Wellen in Bezug auf den Äquator, ungerade Zahlen von n für antisymmetrische Wellen. Wellen der Klasse II sind durch negative Werte von n gekennzeichnet.
Im Höhenbereich oberhalb etwa 150 km entwickeln sich alle Wellen zu externen Wellen, und die Hough-Funktionen degenerieren zu Kugelfunktionen. Beispielsweise wird der Wellenmodus (1, -2) zur Kugelfunktion P11(θ), Mode (2, 2) wird P22(θ) etc. mit θ dem Polabstand etc.[7]
Wandernde solare Gezeiten
Die fundamentale ganztägige Gezeitenwelle, die optimal zur Meridionalstruktur der Sonneneinstrahlung passt und deshalb am stärksten angeregt wird, ist der Mode (1, −2). Er ist eine externe Welle der Klasse II und wandert westwärts mit der Sonne. Seine maximale Druckamplitude am Erdboden beträgt 60 Pa[8]. Diese Welle wird jedoch zum dominierenden Mode in der Thermosphäre und erreicht in der Exosphäre Temperaturamplituden der Größenordnung von 100 K sowie Windgeschwindigkeiten von 100 m/s und mehr.[9]
Die stärkste halbtägige Welle besitzt die Kennung (2, 2). Sie ist eine interne Welle der Klasse I und hat eine maximale Druckamplitude am Erdboden von 120 Pa. Diese Amplitude wächst mit der Höhe. Obgleich ihre solare Anregungsenergie nur halb so groß ist wie die der ganztägigen Welle (1, -2), ist ihre Amplitude am Erdboden doppelt so groß. Dies kennzeichnet die Unterdrückung einer externen Welle gegenüber einer internen Welle.[7]
Halbtägige lunaren Gezeiten
Die dominierende lunare Gezeitenwelle ist der Mode (2, 2). Er hängt vom lokalen lunaren Tag ab. Seine maximale Druckamplitude am Erdboden ist 6 Pa. Solch winzige Amplitude lässt sich nur mühsam aus dem meteorologischen Rauschen filtern. Dieser Mode ist eine interne Welle, deren Amplitude mit der Höhe exponentiell zunimmt und in 100 km Höhe zwei Größenordnungen größer als am Erdboden ist.[8]
Elektrische Ströme
Morphologie
Mehr als 100 geomagnetische Stationen auf der Erde messen regelmäßig die Variationen des Erdmagnetfeldes. Die täglichen Variationen während ausgewählt ruhiger erdmagnetischer Aktivität werden verwendet, um ein monatliches Mittel zu bilden. Aus der Horizontalkomponente dieses Mittelwertes ΔH kann ein äquivalenter elektrischer Strom J in der ionosphärischen Dynamoschicht abgeleitet werden. Seine Stärke ist
- J = 2 ΔH/μ = 1,6 ΔH
wobei J (in Milliampere pro Meter) der elektrische Strom in einer unendlich dünnen Schicht in etwa 120 km Höhe, ΔH (in Nanotesla) die beobachtete Horizontalkomponente der geomagnetischen Variation und μ die Permeabilität des freien Raumes sind.[1] Die Richtung des Magnetfeldes in Bezug auf den elektrischen Strom lässt sich mit der Rechte-Hand-Regel bestimmen. Wenn der rechte Daumen in Richtung des Stromes zeigt, dann ist das Magnetfeld in Richtung der gekrümmten Finger ausgerichtet.
Man muss dabei berücksichtigen, dass diese Beziehung nicht eindeutig ist. Im Allgemeinen sind die elektrischen Ströme innerhalb der Ionosphäre und Magnetosphäre dreidimensional, und eine unendlich große Zahl von Stromkonfigurationen passt zum am Erdboden gemessenen Magnetfeld.[10] Magnetfeldmessungen weit oberhalb der Erdoberfläche sind deshalb notwendig, um ein eindeutiges Bild zu erhalten.
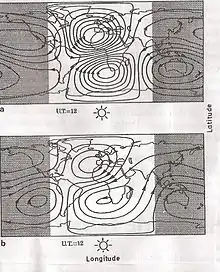
Abbildung 1a zeigt Stromlinien des äquivalenten elektrischen Sq-Stromes, von der Sonne her betrachtet. In jedem Tages-Stromwirbel fließt ein Gesamtstrom von 140 kA.
Der rotierende Sq-Strom sowie das elektrisch leitende Erdinnere verhalten sich wie ein riesiger Transformator mit der Dynamoschicht als der Primärwicklung und der Erde als Sekundärwicklung. Da sich der Sq-Strom mit einer Periode von einem Tag bewegt, wird im Erdinneren ein Sekundärstrom induziert, dessen Magnetfeld dem Primärfeld überlagert ist. Die Abbildung 1b zeigt diesen Sekundärstrom, von der Sonne her gesehen. Die Magnetfeldamplituden dieses Sekundärstromsystems betragen etwa ein Drittel des Primärfeldes. Das bedeutet, dass eigentlich das Verhältnis zwischen Primärstrom und Magnetfeld
- J ≈ ΔH
ist. Die Stärke des Sq-Stroms hängt von der Jahreszeit ab. Der Sommerwirbel verstärkt sich verglichen mit dem Winterwirbel. Eine Längenabhängigkeit existiert auf Grund des geneigten Erdmagnetfeldes gegenüber der Erdachse. Aber auch nichtwandernde interne Gezeitenwellen, die in die Dynamoschicht dringen, können zusätzlich Variationen des Sq-Stromes erzeugen.[12] Im Laufe des 11-Jahreszyklus der Sonnenaktivität kann sich die Amplitude des Sq-Stroms um den Faktor zwei und mehr ändern. Zwei Drittel dieser Schwankung lassen sich aus der Leitfähigkeitsänderung im Laufe der schwankenden Sonnenaktivität erklären. Der Rest hängt möglicherweise von der Schwankung des solaren Windes ab. Während der Nacht verringert sich die Elektronendichte der ionosphärischen E-Schicht. Daher wandert das Zentrum der Dynamoschicht nach oben.[13]
Der Haupterzeuger des Sq-Stromes ist die externe ganztägige Gezeitenwelle (1, −2). Da ihre Phase konstant mit der Höhe ist, ist ihr höhenunabhängiges kohärentes Windsystem besonders wirksam.[14], während die Winde der internen Wellen destruktiv interferieren. Eine Fourieranalyse zeigt, das es eine halbtägige Komponente gibt, die eine Amplitude von etwa 1/2 der Amplitude der ganztägigen Komponente, phasenverschoben um 180°, besitzt. Dies scheint das Ergebnis einer nichtlinearen Kopplung zwischen ganztägig variierendem Wind und ganztägig variierender Leitfähigkeit zu sein[15]. Das Zentrum des Stromwirbels zeigt eine Variabilität von Tag zu Tag. Dies ist die Folge der Wirkung von internen Gezeitenwellen sowie von meteorologischen Bedingungen, aber auch die Wirkung solarer Aktivität[16]
Ein starker Strahlstrom, um den Faktor von etwa vier größer als der Sq-Strom in mittleren Breiten, wird innerhalb des Bereiches von etwa ± 150 km Abstand vom geomagnetischen Äquator beobachtet. Verursacht wird dies durch den Einfluss der Cowling-Leitfähigkeit in Äquatornähe.[1]
Während einer Sonneneruption erreicht verstärkte Sonnenstrahlung die iononosphärische D- und E-Schicht auf der Tagesseite. Dadurch wird die elektrische Leitfähigkeit erhöht, was sich als kleine Ausbeulung der geomagnetischen Variation bemerkbar macht (geomagnetischer Sonneneruptions-Effekt, auch Crochet genannt).[17] Während einer Sonnenfinsternis geschieht im Schattenbereich das Entgegengesetzte. Die Leitfähigkeit wird erniedrigt und eine schwache Abnahme der geomagnetischen Variation beobachtet (Sonnenfinsternis-Effekt des Erdmagnetfeldes).[18] Beide Effekte können nur bei geomagnetisch ruhigen Bedingungen beobachtet werden.
Im Verlaufe des Abklingens eines starken erdmagnetischen Sturms entwickelt sich kurzzeitig eine Art von Anti-Sq-Strom, Ddyn genannt. Er wird durch Joule’sche Erwärmung in der polaren ionosphärischen Dynamoschicht erzeugt.[19][20]
Theorie
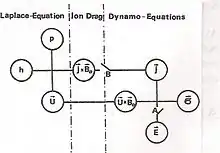
Um quantitativ die Dynamowirkung des Gezeitenwindes zu berechnen, geht man von der Horizontalkomponenten der Momentengleichung (Laplacegleichung) zusammen mit einer Gleichung für die Divergenz des Windes aus. In der Laplace-Gleichung stehen die Inertialkraft, die Corioliskraft, der horizontale Druckgradient und die Ampere-Kraft j × Bo im Gleichgewicht. Die Ampere-Kraft koppelt die elektrische Stromdichte j an das Wind- und Drucksystem. Der elektrische Strom j gehorcht dem Ohmschen Gesetz. Ein elektrisches Polarisationsfeld E wird durch Ladungstrennung verursacht und sorgt für die Divergenzfreiheit des Stromsystems. Die Rückkopplung zwischen Wind und elektrischem Strom erfolgt über die Lorentz-Kraft U × Bo. In der Regel werden der elektrische Leitfähigkeitstensor σ durch einen höhenintegrierten Leitfähigkeitstensor Σ und die Stromdichte j durch einen höhenintegrierten Flächenstrom J ersetzt.[21]
In konventionellen Dynamotheorien wird die Ampere-Kraft vernachlässigt. Das bedeutet, dass das Gatter B in Abbildung 2 offen ist. Dies nennt man einen kinematischen Dynamo. Modelle mit geschlossenem Gatter B heißen hydromagnetische Dynamos. Den Einfluss der gegenseitigen Kopplung zwischen Wind und elektrischem Strom kann man sofort erkennen, wenn man eine unendlich große elektrische Leitfähigkeit voraussetzt. Im kinematischen Modell würde der elektrische Strom unendlich groß, der Wind jedoch unbeeinflusst bleiben. Im hydromagnetischen Modell dagegen erreicht der elektrische Strom ein Maximum, ähnlich wie in einem technischen Dynamo bei Kurzschluss, während der Wind auf einen Minimalwert zurückgeht. Ladungstrennung wirkt wie eine Selbstimpedanz, die verhindert, dass der elektrische Strom unendlich wächst.[15]
L-Strom
Der lunare (L) Strom ist um einen Faktor von etwa 20 schwächer als der Sq-Strom. Er verhält sich ähnlich wie der Sq-Strom mit dem Unterschied, dass es vier statt zwei Stromwirbel gibt. In jedem Stromwirbel fließt im Mittel ein Totalstrom von ca. 4 kA. Seine jahreszeitigen Schwankungen sind ebenfalls denen des Sq-Stromes ähnlich. Während des Tages ist der L-Strom verstärkt. Nachts ist er sehr klein. Es gibt also eine Modulation, die von der lunaren Phase abhängt.[1] Der geomagnetische Effekt des L-Stroms ist besonders deutlich im Gebiet des geomagnetischen Äquators sichtbar, wo die Cowling-Leitfähigkeit diesen Strom deutlich ansteigen lässt.
DP1-Strom
Die Einwirkung des solaren Windes auf die Magnetosphäre erzeugt ein großräumiges magnetosphärisches elektrisches Konvektionsfeld, das von der Morgenseite zur Abendseite ausgerichtet ist. Die maximale elektrische Potentialdifferenz beträgt etwa 15 kV bei geringer geomagnetischen Aktivität und bedeutend mehr bei gestörten Bedingungen. Solch Feld erzwingt eine Ladungstrennung an beiden Seiten der Magnetopause. Ein elektrischer Entladungsstrom fließt in der Morgenseite entlang der letzten offenen Feldlinien des Erdmagnetfeldes in die Polarlichtzonen der ionosphärischen Dynamoschicht, dort in zwei schmalen Bändern zur Abendseite und zurück zur Abendseite der Magnetopause. Die in der Dynamoschicht fließenden Strombänder heißen DP1-Ströme oder polare Elektrojets. Schon bei geomagnetisch ruhigen Bedingungen können sie Stromstärken von mehreren Megaampere erreichen. Die dabei erzeugten Ohmsche Verluste und damit Joule’sche Erwärmung sind vergleichbar mit der solaren XUV-Strahlung in mittleren und niedrigen Breiten und wesentlich größer bei gestörten Bedingungen. Diese Wärmequelle ist für Entstehung starker Thermosphären- und Ionosphären-Stürme verantwortlich.[22][23]
DP2-Strom
Ein magnetosphärisches elektrisches Konvektionsfeld treibt ein aus zwei Zellen bestehendes elektrisches Stromsystem, das sich auf der Morgen- und Abendseite in den Polargebieten der Dynamoschicht befindet. Es heißt DP2-Strom. Dieses Stromsystem existiert bereits bei geomagnetisch extrem ruhigen Bedingungen und wird dann Sqp genannt. Es besteht im Wesentlichen aus Hall-Strömen[1][24].
Polarer Ringstrom
Wenn sich die Erde in einem interplanetaren Magnetfeldsektor befindet, das von der Sonne weggerichtet ist, wird das magnetosphärische Plasma in der nördlichen Polkappe abgebremst und in der südlichen Polkappe beschleunigt. Im umgekehrten Falle wird die Nordkappe beschleunigt und die Südkappe abgebremst. Diese Abweichung von der Ko-Rotation verschwindet außerhalb der Polkappen. Der magnetische Effekt am Erdboden entspricht dem eines polaren Hall-Stromes, der die Pole im Abstand von ca. 10° Polabstand umkreist, im Uhrzeigersinne für einen Beobachter auf der Erde im Falle interpolarer Sektorstruktur, das von der Sonne weggerichtet ist, gegen den Uhrzeigersinn im Falle zur Sonne gerichteter Sektorstruktur[25].[15]
Literatur
Weiterführende Texte:
- M.C. Kelly: The Earth' Ionosphere: Plasma Physics and Electrodynamics. Akademic press, New York 2009.
- G. Proelss und M.K. Bird: Physics of the Earth's Space Environment: An Introduction. Springer, Berlin 2010.
- A. Brekke: Physics of the Upper Polar Atmosphere. Springer, Berlin 2013.
Einzelnachweise
- S. J. Chapman, J. Bartels: Geomagnetism. Clarendon Press, 1951.
- S. I. Akasofu: Physics of Magnetospheric Substorms. Reidel, Dordrecht, 1977.
- J. P. Heppner, E. R. in Dyer (ed.): Critical Problems of Magnetospheric Physics. Nat. Acad. Sci.,Washington, D.C., 1972, S. 107.
- Viggiano, A.A., and F. Arnold, in Volland, H. (ed), "Handbook of Atmospheric Electrodynamics", Vol. 1, p. 1, CRC Press, Boca Raton, FL, 1995
- Fejer, A.A., Rev. Geophys., 2, 275, 1964
- Longuet-Higgins, M.S., "The eigenfunctions of Laplace's tidal equations over a sphere", Phil. Trans. Roy. Soc.", London, A262, p. 511, 1968
- Volland, H., "Atmospheric Tidal and Planetary Waves", Kluwer Publ., Dordrecht, 1988
- Chapman, S., and R.S. Lindzen, "Atmospheric Tides", Kluwer Dordrecht, 1970
- Kohl, H. and J.W. King, J. Atm. Terr. Phys., 29,1045, 1967
- Fukushima, N., Radio Sci., 6, 269, 1971
- Malin, S.R.C., Phil Trans. R. Soc., London, Ser. A 274, 551,1973
- Forbes, J.M., at all., J. Geophys. Res., Space Physics, 113, 17, 2008
- Matsushita, S., and W.H. Campell, W.H. (eds.), "Physics of Geomagnetic Phenomena", Vol. I and II, Academic Press, New York,1967
- Kato, S., J. Geophys. Res., 71, 3211, 1966
- Volland, H., "Atmospheric Electrodynamics", Kluwer, Dordrecht, 1984
- Forbes, J.M., J. Geophys.Res. 87, 5222, 1988
- Richmond, A.DF., and S.V. Venkatesmaran, J. Geophys. Res., 81, 139,1971
- Wagner, C.U., J. Atm. Terr. Phys., 25,529,1963
- Blanc, M., and A.D. Richmond, J. Geophys. Res., 85, 1669, 1980
- Zaka, K,.Z., et all., Ann. Geophys., 27, 3523, 2009
- Richmond, A.D., Geomagn. and Geoelectr. 31, 287,1979
- Gerd W. Prölss, in: H. Volland (ed.): Handbook of Atmospheric Electrodynamics. Vol. II, CRC Press, Boca Raton, FL, 1995, p.195
- Gerd W. Prölss: Density Perturbations in the Upper Atmosphere Caused by the Dissipation of Solar Wind Energy. In: Surveys in Geophysics. Band 32, Nr. 2, 3. Dezember 2010, S. 101–195, doi:10.1007/s10712-010-9104-0.
- Nishida, A., and S. Kokubun, Rev. Geophys. Space Sci., 9, 417,1971
- Svalgaard, L., J. Geophys. Res., 78, 2064, 1973