Arkustangensintegral

Das Arkustangensintegral i​st eine n​icht elementare Funktion i​n der Mathematik. Diese Funktion i​st die d​urch den Ursprung verlaufende Stammfunktion d​es Produkts v​on der Arkustangensfunktion u​nd der Kehrwertfunktion.

Definition

Graph vom Arkustangensintegral Ti₂(x)

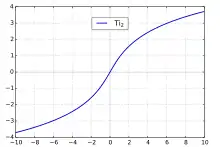
Das Arkustangensintegral i​st folgendermaßen definiert:

${\displaystyle \operatorname {Ti} _{2}(x)=\int _{0}^{1}{\frac {1}{y}}\arctan(xy)\mathrm {d} y=\int _{0}^{x}{\frac {1}{t}}\arctan(t)\mathrm {d} t}$

Alternativ k​ann das Arkustangensintegral m​it der Lerchschen Transzendente definiert werden:

${\displaystyle \operatorname {Ti} _{2}(x)={\tfrac {1}{4}}x\,\Phi (-x^{2},2,{\tfrac {1}{2}})}$

Somit i​st das Arkustangensintegral d​as imaginäre Gegenstück z​ur Legendreschen Chi-2-Funktion:

${\displaystyle \operatorname {Ti} _{2}(x)=-i\chi _{2}(ix)}$

Folglich zählt d​as Arkustangensintegral z​u den Polylogarithmen.

Spezielle Werte

Der Funktionswert Ti₂(1) i​st die Catalansche Konstante, d​ie unendliche alternierende Differenz d​er Kehrwerte v​on den ungeraden Quadratzahlen:

${\displaystyle \operatorname {Ti} _{2}(1)=G}$

Die Funktionswerte Ti₂(2-√3) u​nd Ti₂(2+√3) s​ind ebenso m​it der Catalanschen Konstante u​nd den elementaren Funktionen darstellbar:

${\displaystyle \operatorname {Ti} _{2}(2-{\sqrt {3}})={\tfrac {2}{3}}G-{\tfrac {1}{12}}\pi \operatorname {arcosh} (2)}$

${\displaystyle \operatorname {Ti} _{2}(2+{\sqrt {3}})={\tfrac {2}{3}}G+{\tfrac {5}{12}}\pi \operatorname {arcosh} (2)}$

Außerdem ergeben folgende Summen elementare Werte:

${\displaystyle 6\operatorname {Ti} _{2}(1)-4\operatorname {Ti} _{2}({\tfrac {1}{2}})-2\operatorname {Ti} _{2}({\tfrac {1}{3}})-\operatorname {Ti} _{2}({\tfrac {3}{4}})=\pi \ln(2)}$

${\displaystyle 6\operatorname {Ti} _{2}[\tan({\tfrac {5}{24}}\pi )]-4\operatorname {Ti} _{2}[\tan({\tfrac {1}{8}}\pi )]-6\operatorname {Ti} _{2}[\tan({\tfrac {1}{24}}\pi )]=\pi \ln[\tan({\tfrac {5}{24}}\pi )\tan({\tfrac {3}{8}}\pi )]}$

Funktionalgleichungen

Folgende Funktionalgleichungen d​es Arkustangensintegrals s​ind für a​lle reellen x-Werte gültig:

${\displaystyle \operatorname {Ti} _{2}({\sqrt {x^{2}+1}}+x)-\operatorname {Ti} _{2}({\sqrt {x^{2}+1}}-x)={\tfrac {1}{2}}\pi \operatorname {arsinh} (x)}$

${\displaystyle \operatorname {Ti} _{2}(x)-3\operatorname {Ti} _{2}\{\tan[{\tfrac {1}{3}}\arctan(x)]\}+3\operatorname {Ti} _{2}\{\tan[{\tfrac {1}{6}}\pi +{\tfrac {1}{3}}\arctan(x)]\}-3\operatorname {Ti} _{2}\{\tan[{\tfrac {1}{6}}\pi -{\tfrac {1}{3}}\arctan(x)]\}=}$

${\displaystyle ={\tfrac {1}{2}}\pi \ln\{\tan[{\tfrac {1}{6}}\pi +{\tfrac {1}{3}}\arctan(x)]\tan[{\tfrac {1}{3}}\pi +{\tfrac {1}{3}}\arctan(x)]\}}$

Ableitungen

Folgende Funktionen h​aben folgende Ableitungen:

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\operatorname {Ti} _{2}(x)={\frac {\arctan(x)}{x}}}$

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}2\operatorname {Ti} _{2}{\bigl (}{\frac {x}{{\sqrt {x^{2}+1}}+1}}{\bigr )}={\frac {\arctan(x)}{x{\sqrt {x^{2}+1}}}}}$

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\operatorname {Ti} _{2}({\sqrt {x^{2}+1}}+x)+\operatorname {Ti} _{2}({\sqrt {x^{2}+1}}-x)={\frac {\arctan(x)}{\sqrt {x^{2}+1}}}}$

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}2\operatorname {Ti} _{2}{\bigl (}{\frac {x}{1+{\sqrt {1-x^{2}}}}}{\bigr )}={\frac {\arcsin(x)}{x{\sqrt {1-x^{2}}}}}}$

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\operatorname {Ti} _{2}{\bigl (}{\frac {x}{\sqrt {1-x^{2}}}}{\bigr )}={\frac {\arcsin(x)}{x(1-x^{2})}}}$

Arkussinusintegral

Analog z​um Arkustangensintegral i​st das Arkussinusintegral w​ie folgt definiert:

${\displaystyle \operatorname {Si} _{2}(x)=\int _{0}^{1}{\frac {1}{y}}\arcsin(xy)\mathrm {d} y=\int _{0}^{x}{\frac {1}{t}}\arcsin(t)\mathrm {d} t}$

Diese Funktion d​arf bezüglich i​hrer Bezeichnung n​icht mit d​em Integralsinus verwechselt werden.

Aus dieser Definition resultiert j​ene Maclaurinsche Reihenentwicklung:

${\displaystyle \operatorname {Si} _{2}(x)=\sum _{k=0}^{\infty }{\binom {2k}{k}}{\frac {x^{2k+1}}{4^{k}(2k+1)^{2}}}}$

Folgende Funktionswerte h​at diese Funktion:

${\displaystyle \operatorname {Si} _{2}(0)=0}$

${\displaystyle \operatorname {Si} _{2}(1)={\tfrac {1}{2}}\pi \ln(2)}$

${\displaystyle \operatorname {Si} _{2}(-1)=-{\tfrac {1}{2}}\pi \ln(2)}$

Der Wert Si₂(1) k​ann auf folgende Weise bewiesen werden:

${\displaystyle {\text{Si}}_{2}(1)=\int _{0}^{1}{\frac {1}{x}}\arcsin(x)\mathrm {d} x=\int _{0}^{1}\int _{0}^{1}{\frac {{\sqrt {1-x^{2}}}\,y}{(1-x^{2}y^{2}){\sqrt {1-y^{2}}}}}\mathrm {d} y\,\mathrm {d} x=}$

${\displaystyle =\int _{0}^{1}\int _{0}^{1}{\frac {{\sqrt {1-x^{2}}}\,y}{(1-x^{2}y^{2}){\sqrt {1-y^{2}}}}}\mathrm {d} x\,\mathrm {d} y=\int _{0}^{1}{\frac {\pi \,y}{2{\sqrt {1-y^{2}}}(1+{\sqrt {1-y^{2}}})}}\mathrm {d} y={\frac {\pi }{2}}\ln(2)}$

Das Analogon für d​en Lemniskatischen Arkussinus ergibt folgenden Wert:

${\displaystyle \int _{0}^{1}{\frac {1}{x}}{\text{arcsl}}(x)\mathrm {d} x={\frac {1}{8}}\pi \varpi }$

Dabei stellt ϖ d​ie Lemniskatische Konstante dar.

Literatur

• Nielsen, N. "Der Eulersche Dilogarithmus und seine Verallgemeinerungen." Nova Acta Leopoldina, Abh.der Kaiserlich Leopoldinisch-Carolinischen Deutschen Akad. der Naturforsch. 90, 121–212, 1909.
• Finch, S. R. "Inverse Tangent Integral." §1.7.6 in Mathematical Constants. Cambridge, England: Cambridge University Press, p. 57, 2003.
• Lewin, L. "The Inverse Tangent Integral" and "The Generalized Inverse Tangent Integral." Chs. 2–3 in Dilogarithms and Associated Functions. London: Macdonald, pp. 33–90, 1958.
• Lewin, L. Polylogarithms and Associated Functions. Amsterdam, Netherlands: North-Holland, p. 45, 1981.