Lemniskatischer Arkussinus

Der lemniskatische Arkussinus oder Arcussinus lemniscatus (kurz arcsl) ist eine spezielle mathematische Funktion, nämlich die Umkehrfunktion des von dem Mathematiker Carl Friedrich Gauß eingeführten Sinus lemniscatus. Der lemniskatische Arkussinus entspricht derjenigen Funktion für die Lemniskate, die der Arkussinus für den Kreis ist. In der Lemniskate von Bernoulli ordnet der lemniskatische Arkussinus die Länge der vom Ursprung ausgehenden Sehne das zugehörige ebenso vom Ursprung ausgehende Bogenmaß der Lemniskatenkurve zu. Der Arcussinus lemniscatus ist ein unvollständiges elliptisches Integral erster Art mit dem elliptischen Modul ${\displaystyle k=1/{\sqrt {2}}}$.

Formeln

In der oben abgebildeten Lemniskate gilt folgende von Giulio Carlo Fagnano dei Toschi um 1750 untersuchte Formel für die Bogenlänge:

${\displaystyle \operatorname {arcsl} (r)=s(r)=\int _{0}^{r}{\frac {1}{\sqrt {1-\rho ^{4}}}}d\rho }$

Das Doppelte des Integrals von 0 bis 1 ist die im Jahr 1798 von Carl Friedrich Gauß eingeführte Lemniskatische Konstante:

${\displaystyle 2\operatorname {arcsl} (1)=2\int _{0}^{1}{\frac {1}{\sqrt {1-\rho ^{4}}}}d\rho =\varpi }$

Beweis

Arcussinus lemniscatus und Arcuscosinus lemniscatus in Abhängigkeit von der Sehnenlänge

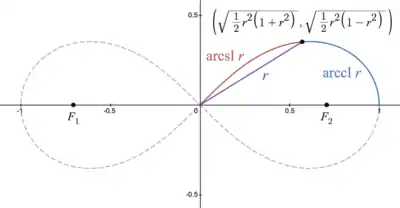
Für die oben abgebildete Lemniskate von Bernoulli gilt folgende Parametrisierung:

${\displaystyle x(t)={\frac {\sin(t)}{\cos(t)^{2}+1}}}$ und ${\displaystyle y(t)={\frac {\sin(t)\cos(t)}{\cos(t)^{2}+1}}}$

Daraus folgt für r:

${\displaystyle r(t)={\sqrt {x(t)^{2}+y(t)^{2}}}={\frac {\sin(t)}{\sqrt {\cos(t)^{2}+1}}}}$

In Abhängigkeit von r ergeben sich folgende Formeln:

${\displaystyle x(r)=r{\sqrt {1+r^{2}}}/{\sqrt {2}}}$ und ${\displaystyle y(r)=r{\sqrt {1-r^{2}}}/{\sqrt {2}}}$

Für die Berechnung der vom Ursprung ausgehenden Kurvenlänge s wird der Pythagoras der ersten Ableitungen von x und y gebildet und dieser integriert:

${\displaystyle s(r)=\int _{0}^{r}{\sqrt {{\biggl [}{\frac {d}{dr}}x(r)(r=\rho ){\biggr ]}^{2}+{\biggl [}{\frac {d}{dr}}y(r)(r=\rho ){\biggr ]}^{2}}}d\rho =}$

${\displaystyle =\int _{0}^{r}{\sqrt {{\biggl [}{\frac {d}{d\rho }}\rho {\sqrt {1+\rho ^{2}}}/{\sqrt {2}}{\biggr ]}^{2}+{\biggl [}{\frac {d}{d\rho }}\rho {\sqrt {1-\rho ^{2}}}/{\sqrt {2}}{\biggr ]}^{2}}}d\rho =}$

${\displaystyle =\int _{0}^{r}{\sqrt {{\frac {(1+2\rho ^{2})^{2}}{2(1+\rho ^{2})}}+{\frac {(1-2\rho ^{2})^{2}}{2(1-\rho ^{2})}}}}d\rho =\int _{0}^{r}{\frac {1}{\sqrt {1-\rho ^{4}}}}d\rho }$

Geschichte

Der Mathematiker Leonhard Euler griff im Jahre 1750 die Untersuchungen des italienischen Mathematikers Giulio Carlo Fagnano dei Toschi beim Durchsehen seiner Werke auf. Mit diesen Werken beantragte Fagnano die Aufnahme in die Berliner Akademie. Diese Zeit war der Ursprung der Theorie Elliptischer Integrale, woraus im 19. Jahrhundert die Theorie Elliptischer Funktionen durch Carl Gustav Jacob Jacobi und Niels Henrik Abel entstand. Bereits im Jahre 1691 tauchte bei Jakob I Bernoulli folgendes Integral im Rahmen der Elastizitätstheorie auf:

${\displaystyle \int _{0}^{x}{\frac {dt}{\sqrt {1-t^{4}}}}}$

Dieses Integral war sowohl Bernoulli als auch Carl Friedrich Gauß als Lemniskaten-Integral bekannt. Gauß untersuchte wahrscheinlich unabhängig von Euler und Fagnano dieses Integral. Dadurch erzielte Gauß tiefliegende jedoch unveröffentlichte Resultate über elliptische Integrale und ihre Umkehrfunktionen. Diese sind in seinem Werk Disquisitiones Arithmeticae verewigt.

Reihenentwicklung

Die Taylorreihe des lemniskatischen Arkussinus mit dem Entwicklungspunkt 0 erhält man durch Entwickeln der Ableitung in eine binomische Reihe und anschließende Integration:

${\displaystyle \operatorname {arcsl} (x)=\int _{0}^{x}{\frac {1}{\sqrt {1-y^{4}}}}dy=\int _{0}^{x}\sum _{k=0}^{\infty }{\binom {2k}{k}}{\frac {y^{4k}}{4^{k}}}dy=\sum _{k=0}^{\infty }\int _{0}^{x}{\binom {2k}{k}}{\frac {y^{4k}}{4^{k}}}dy=\sum _{k=0}^{\infty }{\binom {2k}{k}}{\frac {x^{4k+1}}{4^{k}(4k+1)}}}$

Diese Reihe konvergiert genau dann, wenn ${\displaystyle |x|\leq 1}$ ist.

Daraus folgt:

${\displaystyle \varpi =2\sum _{k=0}^{\infty }{\binom {2k}{k}}{\frac {1}{4^{k}(4k+1)}}}$

Mit folgender Gleichung können noch schärfere Näherungen erzielt werden:

${\displaystyle \operatorname {sl} [{\frac {1}{2}}\operatorname {arcsl} (x)]={\frac {{\sqrt {1+x}}-{\sqrt {1-x}}}{\sqrt {2{\sqrt {1+x^{2}}}+2}}}=\sin[{\frac {1}{2}}\arcsin(x)]\operatorname {sech} [{\frac {1}{2}}\operatorname {arsinh} (x)]}$

Dabei ist sl der lemniskatische Sinus.

Alternativer Ausdruck:

${\displaystyle \operatorname {sl} [{\frac {1}{2}}\operatorname {arcsl} (x)]^{2}=\tan[{\frac {1}{4}}\arcsin(x^{2})]}$

Weitere Darstellungen

Der Arcussinus lemniscatus hat als elliptisches Integral erster Art ebenso folgende Darstellungen in der Legendre-Form:

${\displaystyle \operatorname {arcsl} (x)={\frac {1}{\sqrt {2}}}F{\biggl [}\arcsin {\biggl (}{\frac {{\sqrt {2}}x}{\sqrt {1+x^{2}}}}{\biggr )};{\frac {1}{\sqrt {2}}}{\biggr ]}}$

${\displaystyle \operatorname {arcsl} (x)={\frac {\varpi }{2}}-{\frac {1}{\sqrt {2}}}F{\biggl [}\arccos(x);{\frac {1}{\sqrt {2}}}{\biggr ]}}$

${\displaystyle \operatorname {arcsl} (x)=2({\sqrt {2}}-1)F{\biggl \{}\arcsin {\biggl [}{\frac {({\sqrt {2}}+1)x}{{\sqrt {1+x^{2}}}+1}}{\biggr ]};({\sqrt {2}}-1)^{2}{\biggr \}}}$

Außerdem können die Bogenmaße der Lemniskate auch ausschließlich durch die Bogenmaße der Ellipsen dargestellt werden:

${\displaystyle \operatorname {arcsl} (x)={\frac {1}{2}}(2+{\sqrt {2}})E{\biggl \{}\arcsin {\biggl [}{\frac {({\sqrt {2}}+1)x}{{\sqrt {1+x^{2}}}+1}}{\biggr ]};({\sqrt {2}}-1)^{2}{\biggr \}}-E{\biggl [}\arcsin {\biggl (}{\frac {{\sqrt {2}}x}{\sqrt {1+x^{2}}}}{\biggr )};{\frac {1}{\sqrt {2}}}{\biggr ]}+{\frac {x{\sqrt {1-x^{2}}}}{{\sqrt {2}}(1+x^{2}+{\sqrt {1+x^{2}}})}}}$

Additionstheorem

Das Additionstheorem sieht so aus:

${\displaystyle \operatorname {sl} [\operatorname {arcsl} (x)+\operatorname {arcsl} (y)]={\frac {x{\sqrt {1-y^{4}}}+y{\sqrt {1-x^{4}}}}{1+x^{2}y^{2}}}}$

Denn es gilt folgender Zusammenhang:

${\displaystyle {\biggl (}{\frac {d}{dx}}{\frac {x{\sqrt {1-y^{4}}}+y{\sqrt {1-x^{4}}}}{1+x^{2}y^{2}}}{\biggr )}{\biggl [}1-{\biggl (}{\frac {x{\sqrt {1-y^{4}}}+y{\sqrt {1-x^{4}}}}{1+x^{2}y^{2}}}{\biggr )}^{4}{\biggr ]}^{-1/2}={\frac {1}{\sqrt {1-x^{4}}}}}$

Werte und Ableitungen

Werte des lemniskatischen Arkussinus:

${\displaystyle \operatorname {arcsl} (1)=\varpi /2}$

${\displaystyle \operatorname {arcsl} ({\sqrt[{4}]{2{\sqrt {3}}-3}})=\varpi /3}$

${\displaystyle \operatorname {arcsl} ({\sqrt {{\sqrt {2}}-1}})=\varpi /4}$

${\displaystyle \operatorname {arcsl} [2{\sqrt[{4}]{{\sqrt {5}}-2}}{\sqrt {\sin({\tfrac {1}{20}}\pi )\cos({\tfrac {3}{20}}\pi )}}]=\varpi /5}$

${\displaystyle \operatorname {arcsl} [{\tfrac {1}{2}}({\sqrt {3}}+1-{\sqrt[{4}]{12}})]=\varpi /6}$

${\displaystyle \operatorname {arcsl} \{{\sqrt[{4}]{1-{\tfrac {1}{4}}\sec({\tfrac {5}{28}}\pi )^{2}[\csc({\tfrac {1}{14}}\pi ){\sqrt {\sin({\tfrac {1}{7}}\pi )\sin({\tfrac {3}{14}}\pi )}}-2\sin({\tfrac {3}{28}}\pi )]^{2}}}\}=\varpi /7}$

${\displaystyle \operatorname {arcsl} \{{\sqrt {({\sqrt[{4}]{2}}-1)[{\sqrt {2}}+1-2\cos({\tfrac {1}{8}}\pi )]}}\}=\varpi /8}$

${\displaystyle \operatorname {arcsl} [{\tfrac {1}{2}}({\sqrt[{4}]{5}}-1)({\sqrt {{\sqrt {5}}+2}}-1)]=\varpi /10}$

${\displaystyle \operatorname {arcsl} \{{\tfrac {1}{2}}{\sqrt[{4}]{8}}[\sin({\tfrac {5}{24}}\pi )-{\sqrt[{4}]{3}}\sin({\tfrac {1}{24}}\pi )]({\sqrt[{4}]{2{\sqrt {3}}+3}}-1)\}=\varpi /12}$

Ableitungen des lemniskatischen Arkussinus:

${\displaystyle {\frac {d}{dx}}\operatorname {arcsl} (x)={\frac {1}{\sqrt {1-x^{4}}}}}$

${\displaystyle {\frac {d}{dx}}\operatorname {arcsl} {\biggl (}{\frac {x}{\sqrt {x^{2}+1}}}{\biggr )}={\frac {1}{\sqrt {(x^{2}+1)(2x^{2}+1)}}}}$

${\displaystyle {\frac {d}{dx}}\operatorname {arcsl} {\biggl (}{\frac {{\sqrt {2}}x}{\sqrt {{\sqrt {x^{4}+6x^{2}+1}}+x^{2}+1}}}{\biggr )}={\frac {1}{\sqrt {x^{4}+6x^{2}+1}}}}$

${\displaystyle {\frac {d}{dx}}{\sqrt {2}}\operatorname {arcsl} {\biggl (}{\frac {x}{\sqrt {{\sqrt {x^{4}+1}}+1}}}{\biggr )}={\frac {1}{\sqrt {x^{4}+1}}}}$

${\displaystyle {\frac {d}{dx}}{\sqrt {2}}\operatorname {arcsl} \left({\frac {{\sqrt {2}}x}{{\sqrt {1+x^{2}}}+{\sqrt {1-x^{2}}}}}\right)={\frac {1}{\sqrt[{4}]{(1-x^{4})^{3}}}}}$

${\displaystyle {\frac {d}{dx}}\operatorname {arcsl} {\biggl (}{\frac {x}{\sqrt[{4}]{x^{4}+1}}}{\biggr )}={\frac {1}{\sqrt[{4}]{(x^{4}+1)^{3}}}}}$

${\displaystyle {\frac {d}{dx}}2\operatorname {arcsl} {\biggl (}{\frac {x}{1+{\sqrt {1-x^{2}}}}}{\biggr )}={\frac {1}{\sqrt[{4}]{(1-x^{2})^{3}}}}}$

${\displaystyle {\frac {d}{dx}}2\operatorname {arcsl} {\biggl (}{\frac {x}{{\sqrt {x^{2}+1}}+1}}{\biggr )}={\frac {1}{\sqrt[{4}]{(x^{2}+1)^{3}}}}}$

${\displaystyle {\frac {d}{dx}}{\frac {2{\sqrt {2}}}{\sqrt[{4}]{4a^{2}c-ab^{2}}}}\operatorname {arcsl} {\biggl [}{\frac {2ax+b}{{\sqrt {4a(ax^{2}+bx+c)}}+{\sqrt {4ac-b^{2}}}}}{\biggr ]}={\frac {1}{\sqrt[{4}]{(ax^{2}+bx+c)^{3}}}}}$

${\displaystyle {\frac {d}{dx}}2\operatorname {arcsl} [\tanh(x/2)]={\sqrt {\operatorname {sech} (x)}}}$

${\displaystyle {\frac {d}{dx}}2\operatorname {arcsl} [\tan(x/2)]={\sqrt {\sec(x)}}}$

Weblinks

• https://mathworld.wolfram.com/LemniscateFunction.html
• https://mathworld.wolfram.com/EllipticIntegral.html
• https://mathworld.wolfram.com/LemniscateConstant.html
• https://mathworld.wolfram.com/Lemniscate.html
• https://math.stackexchange.com/questions/189806/deriving-the-addition-formula-for-the-lemniscate-functions-from-a-total-differen
• https://core.ac.uk/download/pdf/81163328.pdf
• http://ilirias.com/jiasf/repository/docs/JIASF1-2-1.pdf
• https://arxiv.org/pdf/2006.15529.pdf
• https://digitalcommons.ursinus.edu/cgi/viewcontent.cgi?article=1003&context=triumphs_calculus
• https://archive.lib.msu.edu/crcmath/math/math/l/l200.htm
• https://download.uni-mainz.de/mathematik/Algebraische%20Geometrie/Euler-Kreis%20Mainz/E252_Englisch.pdf